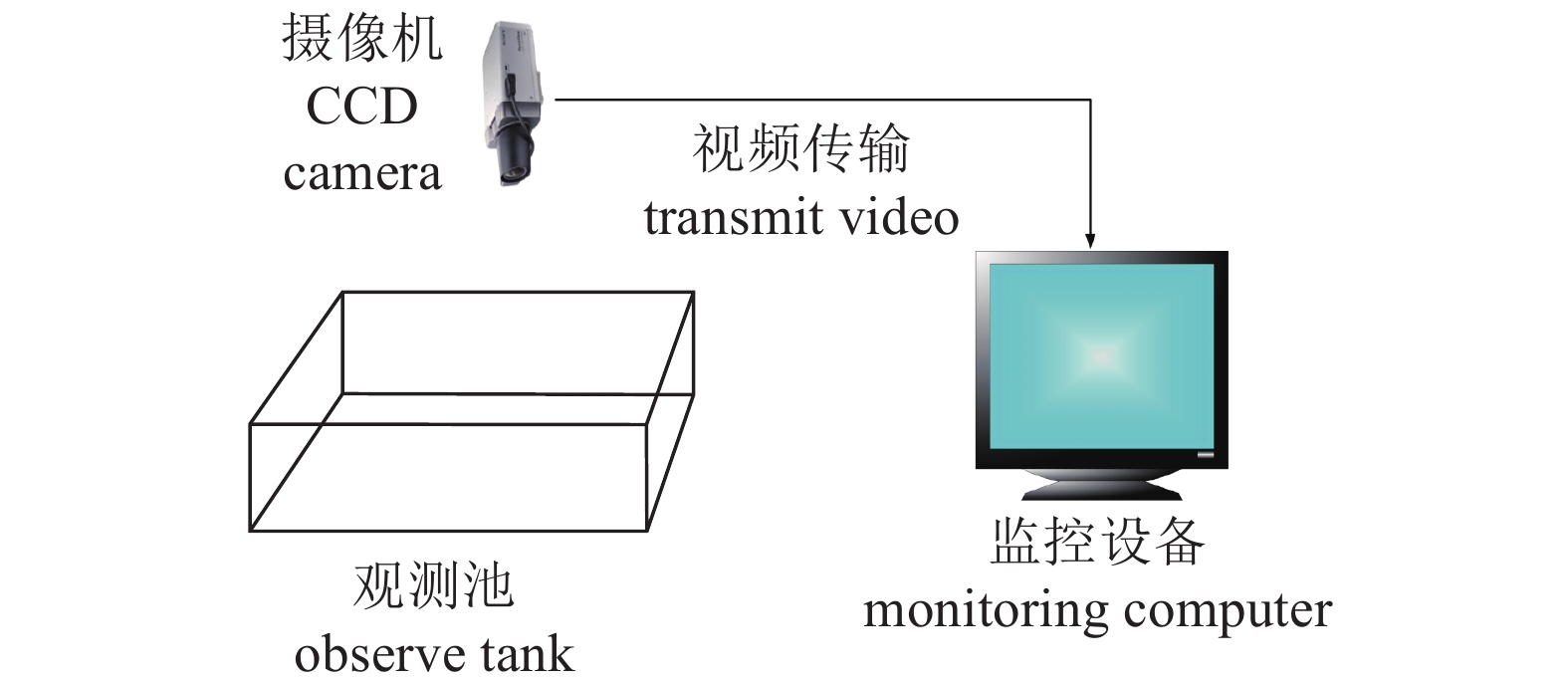
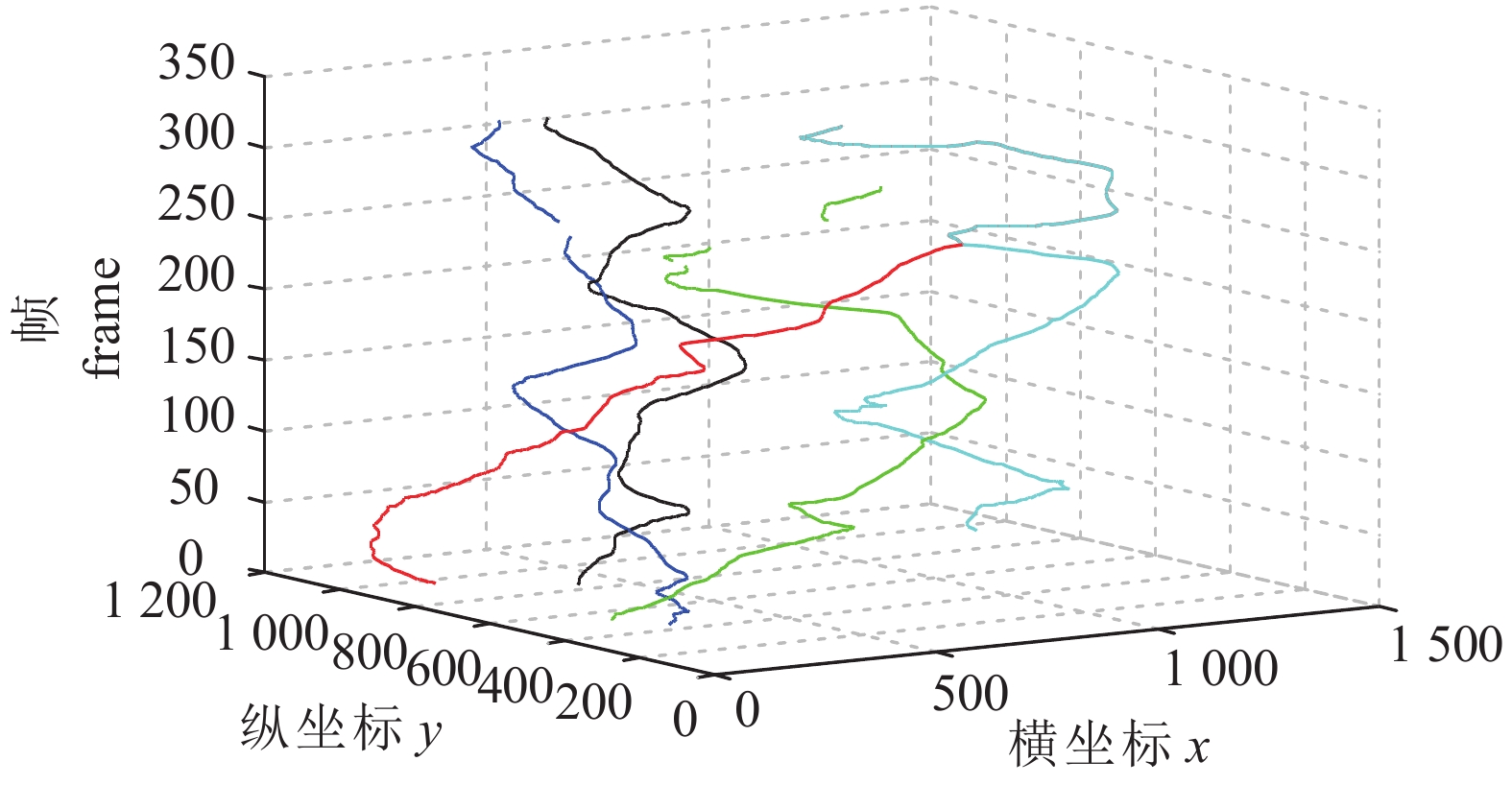
Study on fish movement monitoring method based on image processing
-
摘要: 鱼类运动行为的观察能够为鱼类健康监控提供直观信息,而通过人工标定的方式监测鱼群运动行为耗时长、效率低。文章针对鱼类运动行为的监测问题,提出一种基于图像处理技术的罗非鱼运动监测方法。首先利用计算机、CCD高清摄像机获取鱼群运动视频,再对图像进行滤波去噪、灰度等处理;通过Ostu阈值分割法改进Canny边缘检测算法提取鱼群的边缘轮廓;在建立鱼群运动模型的基础上结合目标关联匹配算法,实现罗非鱼运动行为的跟踪和监测。结果显示鱼群的个体检出率为98.96%,轨迹完整度为97%。提出的算法比卡尔曼滤波的轨迹跟踪监测效果略有提升,能够较好地完成鱼群的运动跟踪和动态监测。Abstract: Observation of fish behavior provides rich visual information for fish health monitoring. However, the method of monitoring the fish behavior by manual marking is time-consuming and inefficient. In order to solve the problem of fish behavior monitoring, a method of monitoring tilapia movement based on image processing is proposed. These fish movement videos were first collected by computer and CCD camera, and then pretreated by graying and filtering. The Canny detection algorithm improved by Otsu was used to extract the edge of fish. Based on modelling the motion of fish school and combining the objective matching algorithm, the tracking and monitoring of fish school can be realized well. The results show that the individual detection rate of fish school was 98.96%, and the trajectory available factor (TAF) was 97%. The proposed algorithm can improve monitoring performance, better than Kalman algorithm, and can realize fish school tracking and monitoring.
-
Keywords:
- fish school /
- movement behavior /
- monitoring /
- image processing /
- extended Kalman filter
-
拖网捕捞是中国目前最重要的捕捞方式之一,东海区海洋捕捞产量占总产量的50%左右[1]。由于渔具选择性相对较差,加之捕捞强度较高,拖网对鱼类资源和群落特征会产生较大影响[1]。有关鱼类群落结构变化的报道和综述已有很多[2-6],并且基本都得到了相似的结论,即在多年持续的高强度捕捞的影响下,鱼类群落的种类多样性呈下降趋势,鱼类小型化、低龄化现象明显。为了保护渔业资源、提高生物多样性,中国每年都在实施伏季休渔政策,而且休渔时间不断延长。而在非休渔季节,中国海洋渔业资源仍然承受着高强度的捕捞压力。休渔和非休渔季节捕捞强度差异十分明显,导致伏季休渔产生的短期性的特点十分明显[7],即当年休渔的成果,由于高强度的捕捞在当年即被摧毁,鱼类群体结构的稳定性较低。这也使对鱼类群落结构在捕捞影响下的短期变化的研究成为可能。
舟山渔场(29°30′~31°00′N,125°00′E以西)位于东海北部、长江口东南外海,在钱塘江口外、长江口渔场之南,为中国最大的近海渔场,是主要经济鱼类重要的产卵地和索饵场,海洋水产资源丰富,吸引诸多渔船在此生产作业。然而自20世纪70年代以来,随着捕捞强度的增加和沿海工业的发展,舟山渔场的渔业资源状况发生了令人担忧的变化:渔业资源的质量下降、数量减少,传统的渔汛季节已无明显界限。进入80年代以后,小黄鱼、大黄鱼、乌贼等已形不成渔汛,带鱼汛亦出现旺汛不旺、网产趋低的现象,严重危及渔业可持续发展[8-9]。尽管舟山渔场是重要的产鱼区,并且面临资源衰退的威胁,但是专门针对该海域的渔业资源和鱼类群落结构开展的研究并不多,近期仅有陈华和徐兆礼[10]以及俞存根等[11]分别对衢山岛海域的鱼类数量变化以及舟山渔场及邻近海域鱼类种类组成和数量分布进行了报道。
中国早在1955年便在渤海、黄海及东海划定了机轮拖网的禁渔区线。1957年和1980年又经过2次增加,形成了全国从北向南由40个基点联线构成的机动渔船拖网禁渔区线;1981年起所有机动底拖网渔船都不得进入上述禁渔区线内作业。因此,拖网只能在禁渔区线以东海域作业。舟山渔场有近一半海域位于禁渔区内,因此,拖网渔船也主要在29°30′~31°00′N,123°00′E~125°00′E的海域生产作业,对这部分海域鱼类群落结构的影响最为明显(图 1)。文章以在舟山渔场禁渔线以外海域作业的单拖网为例,通过2010年4个季度月的调查和渔获物分析资料,使用多样性指数、数量生物量比较(abundance biomass comparison,ABC)曲线和营养级与平均体质量关系等方法,研究这一海域鱼类群落特征周年变化情况,并比较了不同指标对周年内鱼类群落特征变化的指示效果。
1. 材料与方法
1.1 数据来源
资料来自2010年2月、5月、9月和11月单拖网渔船“浙普渔32218”在舟山渔场外缘(图 1)调查及渔获物分析所得数据,每个季度月20网次。渔船主机功率为202 kW,拖网网具规格为960目(140 mm,网口宽度为23.5 m)。拖速约为3 kn。每次随机取样10 kg,装入样品袋,样品放在船舱里低温冰鲜保存,在实验室内进行样品鉴定分析。每次起网后都记下渔获的种类、质量和渔获物总质量,并做好每一网次的渔捞记录。渔获物中的每一种鱼类鉴定到种,并对每一种类进行称质量和尾数计算。渔获数量统一标准化为每小时的渔获量。
1.2 数据分析
按季度月对鱼类群落特征进行研究,计算群落多样性指标,包括Margalef丰富度指数(D)、Shannon-Wiener多样性指数(H′)、Pielou均匀度指数(J′)、Simpson多样性指数(C);同时进行相似性分析,计算Bray-Curtis相似性指数(Bjk)以及Jaccard相似性指数(Jjk);使用ABC曲线进行优势度分析;应用营养级与平均体质量关系(trophic level-average weight)曲线分析鱼类群落营养结构变化。
(1) Margalef丰富度指数:$D=\frac{S-1}{\ln N} $
(2) Simpson多样性指数:$C = \sum\limits_{i = 1}^s {\frac{{n_i^2 - {n_i}}}{{{N^2} - N}}} $
(3) Shannon-Wiener多样性指数:H′= -∑PilnPi
(4) Pielou均匀度指数:$J'=\frac{H^{\prime}}{H_{\max }}=\frac{H'}{\ln S} $
(5) Bray-Curtis相似性指数:${B_{jk}} = \left[ {1 - \frac{{\sum\limits_{i - 1}^s {\left| {n{i_j} - {n_{ik}}} \right|} }}{{\sum\limits_{i - 1}^s {\left( {{n_{ij}} + {n_{ik}}} \right)} }}} \right] \times 100 $
(6) Jaccard相似性指数:$J_{j k}=\frac{a}{a+b+c} \times 100 $
式中S为鱼类种数,ni为第i种鱼的个体数,N为所有鱼类的个体数之和,Pi为第i种鱼占鱼类个体总数的百分比,nij表示第j次取样中第i种鱼的个体数,a表示j和k 2次取样共有的种类数,b表示第j次取样中出现而第k次取样没有出现的种类数,c表示第k次取样中出现而第j次取样没有出现的种类数。
ABC曲线是在同一坐标系中比较生物量优势度曲线和数量优势度曲线,通过2条曲线的分布情况来分析群落不同干扰状况下的特征[12]。ABC曲线的统计量用W统计量表示,公式为:
$$\;\;\;\; W = \sum\limits_{i = 1}^s {\frac{{{B_i} - {A_i}}}{{50(S - 1)}}} $$ 其中S为出现种类数,Bi和Ai分别表示ABC曲线中种类序号对应的质量和数量累积百分比。可见,当质量优势度曲线在上面时W为正,当数量优势度曲线在上面时W为负。
营养级与平均体质量关系是绘制各种类的营养级与其平均体质量的关系图,从而分析各月所捕获不同营养级种类的平均体质量的变化,其中营养级数值来自FishBase网站。
2. 结果
2.1 鱼类组成
调查共鉴定鱼类80种,隶属于13目,49科,59属,其中以鲈形目最多(30种)。渔获物质量组成中所占比例大于1%的鱼类共25种,其中主要经济种类占到50%,数量百分比大于1%的鱼类共23种,以小型低质鱼类为主。4个季节质量百分比和数量百分比排在前10位的鱼类见表 1。质量百分比中绿鳍鱼优势明显,排在第1位(8.29%),前10位中以经济中类为主。数量百分比前3位均为小型非经济种类,并且细条天竺鲷和六丝钝尾虾虎鱼有绝对的数量优势,两者之和达到32.42%。
表 1 舟山渔场禁渔线以外海域4个月质量百分比和数量百分比前10位的鱼类Table 1. First 10 fishes in terms of biomass and abundance percentages for 4 months outside forbidden fishing line of Zhoushan fishing ground种名
species质量百分比/%
biomass percentage种名
species数量百分比/%
abundance percentage绿鳍鱼(Chelidonichthys kumu) 8.29 细条天竺鲷(Apogon lineatus) 19.35 带鱼(Trichiurus haumela) 6.06 六丝钝尾虾虎鱼(Amblychaeturichthys hexanema) 13.07 小黄鱼(Larimichthys polyactis) 5.77 发光鲷(Acropoma japonicum) 8.83 海鳗(Muraenesox cinereus) 5.02 短吻三线舌鳎(Cynoglossus abbreviatus) 7.18 黑 

4.94 小黄鱼(Larimichthys polyactis) 4.98 竹筴鱼(Trachurus japonicus) 4.66 银姑鱼(Pennahia argentatus) 3.92 细条天竺鲷(Apogon lineatus) 4.40 单指虎鲉(Minous monodactylus) 2.83 银姑鱼(Pennahia argentatus) 4.24 绿鳍鱼(Chelidonichthys kumu) 2.63 龙头鱼(Harpodon nehereus) 3.24 带鱼(Trichiurus haumela) 2.55 单指虎鲉(Minous monodactylus) 3.21 竹筴鱼(Trachurus japonicus) 2.55 4个调查月所出现的质量和数量优势种类有所差别,每个调查月质量和数量百分比排在前5位的种类见表 2。质量百分比前5位的鱼类中没有4次调查都出现的种类。其中绿鳍鱼和带鱼出现3次,海鳗、细条天竺鲷和单指虎鲉等出现2次。9月前5位中的经济种类明显多于其他月。数量百分比前5位鱼类中同样没有在4次调查中均出现的种类,出现次数较多的以小型低质鱼类为主,但9月则以经济种类为主。4次调查所取样鱼类的平均体质量差异明显。2月鱼类平均体质量为26.28 g,其中平均体质量不足5 g的有6种,其尾数占该月样品尾数的22.46%,大于50 g的有8种,尾数百分比为13.04%;5月平均体质量最小(8.78 g),平均体质量小于1 g的有3种,体质量不足5 g的有11种,两者尾数百分比高达48.02%,而大于50 g的只有3种,占该月样品尾数的1%;9月平均体质量最大(41.62 g),体质量不足5 g的只有日本鳀和六丝钝尾虾虎鱼2种,其尾数百分比也很低,只有1.85%,大于50 g的鱼类数量最多,有14种,占样品尾数的28.24%;11月平均体质量下降至10.27 g,其中体质量不足5 g的鱼类有5种,而且样品尾数非常高,占总样品数的75.08%,大于50 g的有9种,占样品尾数的4.56%。
表 2 舟山渔场禁渔线以外海域调查月质量百分比和数量百分比前5位鱼类Table 2. First 5 fishes in terms of biomass and abundance percentages for survey months outside forbidden fishing line of Zhoushan fishing ground质量百分比/% biomass percentage 2月February 5月May 9月September 11月November 黑 

20.36 细条天竺鲷(Apogon lineatus) 34.66 竹筴鱼(Trachurus japonicus) 19.04 绿鳍鱼(Chelidonichthys kumu) 12.12 绿鳍鱼(Chelidonichthys kumu) 15.67 带鱼(Trichiurus haumela) 16.98 小黄鱼(Larimichthys polyactis) 18.76 海鳗(Muraenesox cinereus) 9.06 单指虎鲉(Minous monodactylus) 7.52 单指虎鲉(Minous monodactylus) 9.74 带鱼(Trichiurus haumela) 9.84 银姑鱼(Pennahia argentatus) 8.84 带鱼(Trichiurus haumela) 5.91 海鳗(Muraenesox cinereus) 5.34 绿鳍鱼(Chelidonichthys kumu) 7.88 细条天竺鲷(Apogon lineatus) 8.80 前肛鳗(Dysomma anguillaris) 5.30 短吻三线舌鳎(Cynoglossus abbreviatus) 4.48 长蛇鲻(Saurida elongata) 7.64 发光鲷(Acropoma japonicum) 7.32 数量百分比/% abundance percentage 2月February 5月May 9月September 11月November 带鱼(Trichiurus haumela) 15.22 细条天竺鲷(Apogon lineatus) 25.10 小黄鱼(Larimichthys polyactis) 44.91 细条天竺鲷(Apogon lineatus) 67.76 单指虎鲉(Minous monodactylus) 9.42 六丝钝尾虾虎鱼(Amblychaeturichthys hexanema) 21.34 竹筴鱼(Trachurus japonicus) 18.06 发光鲷(Acropoma japonicum) 53.01 中华舌鳎(Cynoglossus sinicus) 8.70 岸上红娘鱼(Lepidotrigla kishinouyi) 10.47 绿鳍鱼(Chelidonichthys kumu) 6.02 银姑鱼(Pennahia argentatus) 7.65 长丝虾虎鱼(Cryptocentrus filifer) 7.97 短吻三线舌鳎(Cynoglossus abbreviatus) 7.51 刺鲳(Psenopsis anontala) 4.17 短吻三线舌鳎(Cynoglossus abbreviatus) 6.56 六丝钝尾虾虎鱼(Amblychaeturichthys hexanema) 5.80 鳄齿鱼(Champsodon capensis) 7.11 带鱼(Trichiurus haumela) 3.70 单指虎鲉(Minous monodactylus) 4.92 2.2 群落的多样性指数
C、H′和J′均呈现出9月以后逐渐升高,随后下降,5月基本达到最低点的趋势,表明经过一年的持续捕捞后,伏季休渔前鱼类群落结构已经变化,群落多样性和鱼类均匀度均降低(图 2)。D在5月值较高,说明5月鱼类种类丰富度较高,这一结果与5月低营养级的小个体种类比例较高相吻合(表 2)。
2.3 多元分析
4个月比较,5月与9月之间的Bjk和Jjk均为最低,即2个月鱼类组成相似性较小,说明5月与9月2次渔获样品的数量和出现的种类均有较大差异(表 3)。
表 3 鱼类组成的相似性指数Table 3. Similarity index of fish composition指数
index相似性指数(Jjk) Jaccard index 2月February 5月May 9月September 11月November Bray-Curtis相似度指数(Bjk)
Bray-Curtis index2月 36.59 37.84 27.91 5月 20.50 24.39 34.15 9月 25.42 10.83 35.14 11月 15.43 36.25 11.81 2.4 绘图特征
2.4.1 ABC曲线
4个月的ABC曲线见图 3。2月质量优势度曲线位于数量优势度曲线之上;5月质量优势度曲线与数量优势度曲线相交;9月和11月数量优势度曲线位于质量优势度曲线之上。2月排在质量优势度和数量优势度曲线前几位的种类变化较大,黑


2.4.2 营养级-平均体质量关系曲线
营养级-平均体质量关系曲线能够反映每个月样品中不同营养级水平鱼类的平均体质量的变化情况。趋势线斜率的绝对值越大,直线越陡,说明高营养级鱼类的平均体质量越高,反之趋势线斜率的绝对值越小,直线越平缓,表明高营养级种类的平均体质量相对较小。比较4个月曲线可以发现,5月曲线斜率绝对值最小,9月最大。将每个月样品中鱼类分为营养级低于3.5、3.5~4.0以及大于4.0共3个类别(图 4)。2月营养级低于3.5鱼类的平均体质量为14.12 g,营养级在3.5~4.0之间鱼类的平均体质量为43.25 g,高于4.0鱼类平均体质量为37.59 g;5月3个类别平均体质量分别为3.48 g、14.39 g和18.28 g;9月为46.68 g、26.41 g和125.56 g;以及11月为8.28 g、18.00 g和70.33 g。不同营养级鱼类平均体质量的变动体现了鱼类群落结构的变化,同时反映了伏季休渔和捕捞影响的结果。伏季休渔之前,即5月各个营养级水平鱼类的平均体质量均为最小;经过伏季休渔后9月各营养级鱼类平均体质量有所增加,特别是高营养级鱼类平均体质量增加明显,并且各营养水平鱼类的平均体质量达到一年中的最大值;之后以大个体经济种类为主要捕捞对象,11月鱼类平均体质量下降,但高营养级种类仍保持较高水平;2月高营养级鱼类平均体质量下降,大个体的中间营养级鱼类增加;至5月经过8个月的持续捕捞,鱼类平均体质量整体降到较低水平。虽然各季度月之间各个营养级水平鱼类的平均体质量变化明显,但每个月3个营养级水平鱼类体质量比例之间的差异并不显著(P=0.296)。
3. 讨论
舟山渔场禁渔线以外海域鱼类组成和群落结构在周年之内已经呈现出较明显的变化。鱼类尤其是高营养级鱼类的平均体质量均在9月最高,随后逐渐下降。多样性指数呈现9月以后逐渐升高,而后又逐渐下降,到5月达到最低。5月和9月捕获鱼类的相似性指数最低,主要由于这两个月渔获样品分别以低质小型鱼类和经济种类为主,从而使得5月和9月鱼类群落结构组成差别最大。调查周年内海洋环境没有剧烈变化,除了鱼类自身的生物学特征变化外,主要是3个半月伏季休渔和持续高强度捕捞共同作用的结果。有研究显示伏季休渔效果的短期性已经十分明显[7, 13-14],虽然休渔时间不断延长,仍难以阻止渔业资源和群落结构的衰退。文章研究结果表明,当前伏季休渔政策对保护幼鱼生长有明显效果,但其成果到年底前后就不复存在,之后的持续捕捞将使鱼类资源量下降,群落中以小型低质鱼类占优。另外,从9月和11月调查结果看,伏季休渔结束以后,高强度的捕捞对高营养级种类影响较大,虽然仍能捕到大个体经济鱼类,而且质量比例较高,但数量明显下降。
单独使用ABC曲线难以判断鱼类群落状况的好坏。ABC曲线受调查渔获样品特征影响较大,即使鱼类群落处于重度干扰,当捕获物中包含几个较大个体或者每种鱼类的数量及质量都没有明显高于其他种类时,质量优势度曲线会高于或接近于数量优势度曲线。体质量是使用最多的表征鱼类生长变化的参数之一,也常用于鱼类群落结构变化的研究中[6, 15-16]。营养级广泛应用于群落和生态系统研究中,常被用来反映鱼类群落中营养格局和结构组成特征[17-18]。同时也有学者提出了营养级在生态学研究中的不足[18]。单独使用营养级对鱼类群落结构的变动进行研究难以全面展现鱼类真实的变化情况。如果相同营养级或同一种鱼类所呈现的平均体质量不同,则其所反映的鱼类群落结构组成是有差异的。文章将营养级与平均体质量相结合来,绘制了鱼类营养级-平均体质量关系图,较好地描述了群落中鱼类组成随时间变化的情况,在分析捕捞影响下鱼类群落结构变化具有一定帮助,特别是对于短期内的变化,比仅使用营养级能更加全面的反映实际问题。
学者们在捕捞对鱼类群落结构和生物多样性造成的影响等问题上已经达成共识并给予了广泛的关注。随着中日和中韩渔业协定的生效,中国在外海生产的船只不得不退出原作业海域[19-20]。并且随着划界谈判的深入,受限制的作业渔场范围越来越广,近海资源相对较好的渔场所面临的形势更加严峻[21]。因此,在今后的工作中需进一步扩大在舟山渔场的研究范围,持续观测鱼类群落结构演变,分析捕捞对其影响的机制,从而为保护舟山渔场的生物多样性,保证渔业资源的可持续利用和渔场健全的生态功能提供更多理论资料。另外,文章主要分析了持续捕捞作用对鱼类群落结构的影响,而对鱼类洄游移动和生长等因素的影响没有作深入的探讨。如4个季度月出现的优势种类差异明显,可能是部分种类移出调查海域,这也会影响到鱼类群落结构的变化。因此,在今后的研究中还要综合考虑多因素的影响,进一步完善分析的结果。
-
表 1 轨迹跟踪统计表
Table 1 Trajectory tracking statistics
方法
method轨迹断裂程度
TFF轨迹完整程度/%
TAF本文方法 extended Kalman algorithm 2.0 97.0 对比方法
Kalman algorithm3.6 93.6 -
[1] 张慧. 鱼类群体行为特性分析及应激仿真技术研究[D]. 舟山: 浙江海洋大学, 2017:1-7. [2] 颜鹏东, 谭均军, 高柱, 等. 基于视频跟踪的竖缝式鱼道内鱼类运动行为分析[J]. 水生生物学报, 2018, 42(2): 250-254. [3] 谭均军, 高柱, 戴会超, 等. 竖缝式鱼道水力特性与鱼类运动特性相关性分析[J]. 水利学报, 2017, 48(8): 924-932. [4] 李相军, 李壮. 地面红外运动目标图像处理与识别算法分析[J]. 舰船电子工程, 2013, 33(5): 53-56. [5] MILLER N, GERLAI R. Quantification of shoaling behaviour in zebrafish (Danio rerio)[J]. Behav Brain Res, 2007, 184(2): 157-166.
[6] 范良忠, 刘鹰, 余心杰, 等. 基于计算机视觉技术的运动鱼检测算法[J]. 农业工程学报, 2011, 27(7): 226-230. [7] 江丹丹, 桂福坤. 基于视频图像的鱼类行为轨迹追踪[J]. 浙江海洋学院学报(自然科学版), 2015, 34(2): 112-118. [8] 朱佩儒, 刘烨, 王硕鸿, 等. 基于学习的斑马鱼检测与跟踪[J]. 计算机应用与软件, 2015, 32(9): 227-230, 250. [9] 张琪, 韩战钢. 一种简单有效的鱼群轨迹追踪算法[J]. 北京师范大学学报(自然科学版), 2017, 53(4): 406-411. [10] TELES L O, FERNANDES M, AMORIM J A. Video-tracking of zebrafish (Danio rerio) as a biological early warning system using two distinct artificial neural networks: probabilistic neural network (PNN) and self-organizing map (SOM)[J]. Aquat Toxicol, 2015, 165: 241-248.
[11] SABERIOON M M, CISAR P. Automated multiple fish tracking in three-dimension using a Structured Light Sensor[J]. Comput Electron Agric, 2016, 121: 215-221.
[12] MAO J F, XIAO G, SHENG W G, et al. Research on realizing the 3D occlusion tracking location method of fish's school target[J]. Neurocomputing, 2016, 214: 61-79.
[13] 石龙伟, 邓欣, 王进, 等. 基于光流法和卡尔曼滤波的多目标跟踪[J]. 计算机应用, 2017, 37(s1): 131-136. [14] 毛家发, 胡海彪, 程振波, 等. 半遮挡目标鱼体的识别与跟踪方法研究[J]. 浙江工业大学学报, 2015, 43(2): 207-211. [15] 李波. 视频序列中运动目标检测与跟踪算法的研究[D]. 北京: 北京交通大学, 2011: 7-16. [16] 孙亮, 李敬文. 一种简单的灰度图像边缘检测算法[J]. 兰州交通大学学报, 2013, 32(1): 111-115. [17] 陈益杉, 卢伟, 王玲, 等. 基于GIF-Shearlet算法的新旧土边界线视觉导航技术研究[J]. 农业现代化研究, 2017, 38(2): 343-351. [18] 郭萌, 胡辽林, 赵江涛. 基于Kirsch和Canny算子的陶瓷碗表面缺陷检测方法[J]. 光学学报, 2016, 36(9): 27-33. [19] GOULART J T, BASSANI R A, MAGALHAES BASSANI J W. Application based on the Canny edge detection algorithm for recording contractions of isolated cardiac myocytes[J]. Comput Biol Med, 2017, 81: 106-110.
[20] JIANG W, ZHOU H, SHEN Y, et al. Image segmentation with pulse-coupled neural network and Canny operators[J]. Comput Electr Eng, 2015, 46: 528-538.
[21] 林国余, 张为公. 基于进化规划的最大类间方差的图像分割算法[J]. 传感技术学报, 2006, 19(1): 179-182. [22] 刘丽娟, 刘仲鹏, 程芳. 玉米生长期叶部病害图像识别预处理研究[J]. 河南农业科学, 2013, 42(10): 91-94. [23] 朱琳, 周杰, 宋靖雁. 一种新的基于在线采样的多物体跟踪方法[J]. 计算机学报, 2008, 31(1): 151-160. [24] KULIKOVA M V, KULIKOV G Y. NIRK-based accurate continuous-discrete extended Kalman filters for estimating continuous-time stochastic target tracking models[J]. J Comput Appl Math, 2016, 316: 260-270.
-
期刊类型引用(8)
1. 赵函磊,王洋,张畅,王迎宾. 混合渔业视角下舟山渔场几种渔具管理策略对经济物种产量及生物群落影响评估. 水生生物学报. 2025(04): 131-143 .  百度学术
百度学术
2. 王春丽,陈峰,蒋日进,张洪亮,朱文斌,朱凯. 典型气候事件对浙江近海底层鱼类时空分布的影响. 生态学报. 2024(10): 4231-4243 .  百度学术
百度学术
3. 苏莹佳,陈国宝,周艳波,马胜伟,吴洽儿. 2015—2017年南海海域伏季休渔制度实施效果评价. 南方水产科学. 2019(02): 20-28 .  本站查看
本站查看
4. 黄吉万,李腾,孙典荣,刘岩,刘胜男,单斌斌,杨长平. 汕尾甲湖湾附近海域鱼类结构季节变动研究. 安徽农业科学. 2018(07): 71-77 .  百度学术
百度学术
5. 范江涛,冯雪,陈作志. 基于水温垂直结构的南海北部近海竹鱼渔场分析. 南方水产科学. 2018(02): 124-128 .  本站查看
本站查看
6. 袁华荣,陈丕茂,秦传新,黎小国,周艳波,冯雪,余景,舒黎明,唐振朝,佟飞. 南海柘林湾鱼类群落结构季节变动的研究. 南方水产科学. 2017(02): 26-35 .  本站查看
本站查看
7. 邹建伟,王强哲,林丕文,黄俊秀. 伏季休渔对北部湾北部虾类捕捞的影响及评价. 南方水产科学. 2015(06): 88-93 .  本站查看
本站查看
8. 陈曦浩,毛雄斌,雷科,陈玲,王迎宾. 基于渔捞日志的舟山渔场单拖网渔获量时空特征分析. 浙江海洋学院学报(自然科学版). 2013(03): 202-207 .  百度学术
百度学术
其他类型引用(8)




 下载:
下载:




 粤公网安备 44010502001741号
粤公网安备 44010502001741号
