A study on sinking and closing performance of falling-net
-
摘要:
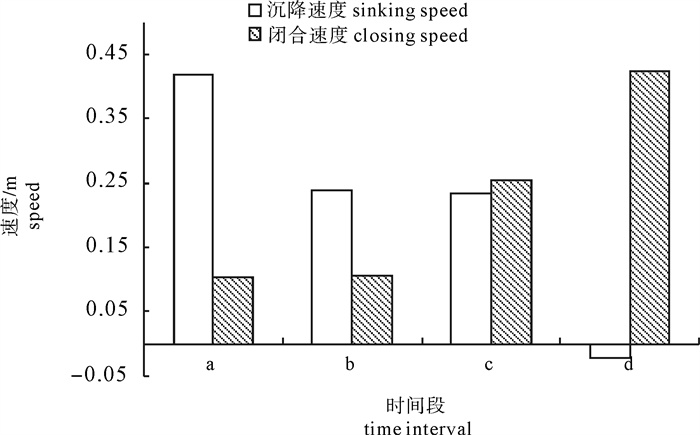
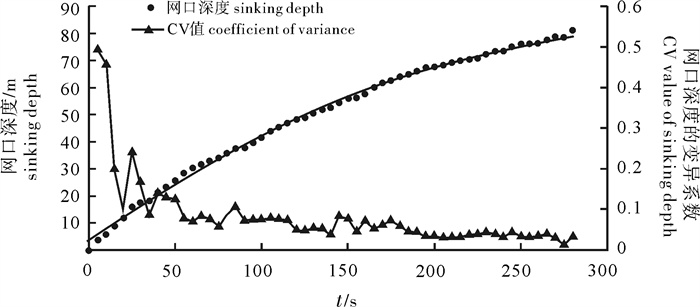
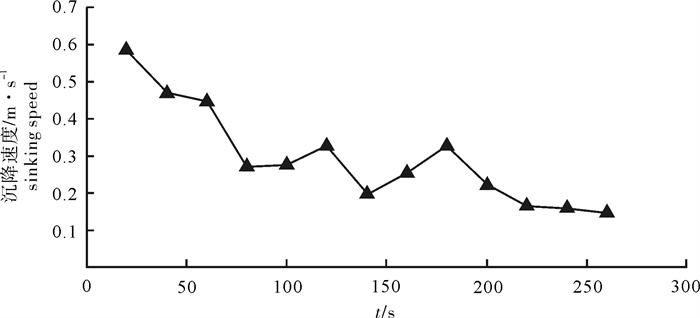
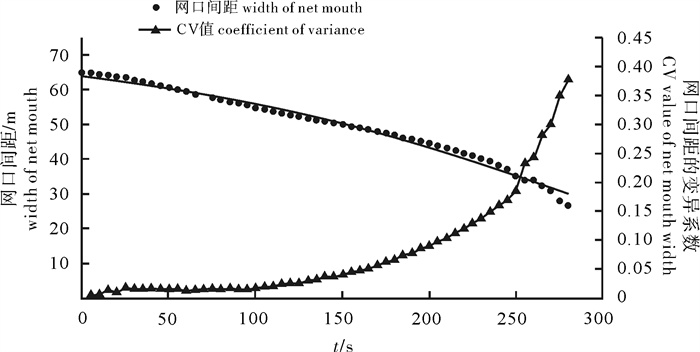
根据2014年11月使用SDKN-500型网位仪所采集的罩网作业时网口深度和间距的实时数据，分析罩网网口沉降与闭合性能。结果发现：1)渔船绞收网口纲后，网口沉降和闭合速度不会马上突变，存在120.7 s的滞后时间；2)网口降至最大深度时(平均82.0 m)，仍未完全闭合，此后深度相对稳定，直至网口完全闭合(平均68.0 s)并停滞一段时间(平均9.8 s)后网口才开始上升；3)渔船不同作业状态可分为开始放网(设为0 s)、开始绞收网口纲(平均104.0 s)、网口加速闭合(平均224.7 s)、网口达最大深度(平均266.6 s)、网口完全闭合(平均334.6 s)，也是决定罩网性能的5个关键时间节点；4)4个时段的网口沉降速度分别为0.419 m · s-1、0.238 m · s-1、0.233 m · s-1和-0.021 m · s-1，总体呈递减趋势，沉降中期存在波动；5)4个时段的网口闭合速度分别为0.103 m · s-1、0.105 m · s-1、0.253 m · s-1和0.424 m · s-1，总体呈递增趋势；整个沉降过程闭合速度在前期先变大后变小，在沉降后期明显加大。建议提高网口纲绞收速度以避免鱼群逃逸。
Abstract:Based on the real-time data of sinking depth and distance of net mouth of falling-net by SDKN-500 net monitor in November 2014, we analyzed the sinking and closing performance of falling-net. The results show that: 1) The sinking and closing speeds would not mutate when pursing the purse line with retardation time of 120.7s;2) The net mouth was not completely closed when it reached the maximum depth (averagely 82.0 m), and did not rise up until it was completely closed (averagely 68.0 s) and stayed for a while (averagely 9.8 s); 3) The different operating conditions could be divided into the shooting time (0 s), the pursing time (averagely 104.0 s), the time when the closing speed mutated (averagely 224.7 s), the time when the net mouth reached the maximum depth (averagely 266.6 s) and the time when the net mouth was completely closed (average 334.6 s) in sequence, which were the five key time nodes determining the fishing performance of falling-net; 4) The sinking speeds of the four periods were 0.419 m · s-1, 0.238 m · s-1, 0.233 m · s-1 and -0.021 m · s-1, respectively, showing a decreasing trend with fluctuation in the middle of settlement; 5) The closing speeds of the four periods were 0.103 m · s-1, 0.105 m · s-1, 0.253 m · s-1 and 0.424 m · s-1, respectively, showing an increasing trend. The closing speed of net mouth increased firstly and then decreased at the beginning of settlement, and the closing speed showed a significant increasing trend in the later period of settlement. It is suggested to increase the hauling speed to avoid fish escape.
-
Keywords:
- falling-net /
- sinking performance /
- closing performance of net mouth
-
金线鱼(Nemipterus virgatus)属金线鱼科、金线鱼属，是南海区重要的经济鱼类[1-2]。2013年南海区金线鱼捕捞产量为317 094 t，占海洋捕捞总产量的9.72%[3]。南海金线鱼的主要作业方式包括底拖网、手钓、延绳钓和流刺网[1, 4-5]。金线鱼刺网属于漂流单片刺网，是南海区重要作业方式，其捕捞种类除金线鱼外，还包括多齿蛇鲻(Saurida tumbil)、长尾大眼鲷(Priacanthus tayenus)、带鱼(Trichiurus haumela)等[5]。目前，南海区金线鱼刺网网目尺寸有不断减小的趋势[5]，且该刺网尚未见有最小网目尺寸的标准或研究报道，仅农业部于2014年以通告的形式规定南海区流刺网最小网目尺寸为50 mm。关于南海金线鱼刺网最小网目尺寸定为50 mm是否合理这一问题，目前尚未见有相关的研究报道。
刺网选择性研究是制定最小网目尺寸的理论基础和前提[6]。目前，刺网选择性研究最常用的方法是间接估算法，即采用几种网目尺寸不同的刺网进行共同捕鱼试验，然后通过比较渔获物的体长变化确定刺网的选择性[6-7]。SELECT(Share Each LEngthclass′s Catch Total)模型于1992年由MILLAR发明并应用于拖网选择性研究中，之后该模型被广泛应用于张网、刺网、笼壶和延绳钓的选择性估算中[8-14]。国外很多刺网选择性研究都以SELECT模型作为参数估算的手段[11, 15-16]。迄今，中国也进行过一些刺网选择性研究[4, 17-18]，但以SELECT模型为基础的不多。尤其基于SELECT模型的金线鱼刺网选择性研究还未见有报道。文章根据南海区金线鱼刺网选择性试验的相关数据，以SELECT模型为基础，分析刺网网目尺寸对金线鱼的选择性，为制定最小网目尺寸提供科学依据，也为SELECT模型在中国刺网选择性研究的应用提供参考。
1. 材料与方法
1.1 试验渔船和渔场
试验于2008年5月在南海北部近海渔场进行。试验渔船为传统金线鱼刺网生产船，船名“粤阳东18023”，船长23.2 m，主机功率183 kW。作业海域经纬度为112° 00′~113° 00′E、20°00′~21°30′N，水深75~87 m，底质为沙泥。
1.2 试验网具
用网目尺寸分别为40 mm、45 mm、50 mm、55 mm和60 mm的金线鱼刺网共47片进行试验，网具的详细参数见表 1。网线材料为锦纶单丝，机械编织。上纲长度为36.97 m，缩结系数为0.51；下纲长度45.45 m，缩结系数为0.63。
表 1 实验网的主要技术参数Table 1. Technical characteristics of gillnets used in this experiment参数parameter 网目尺寸/mm mesh size 40 45 50 55 60 横向目数/目number of mesh in length 1 798 1 598 1 438 1 308 1 198 纵向目数/目number of mesh in height 120 106 96 88 80 上纲长度/m length of floatline 36.97 36.97 36.97 36.97 36.97 下纲长度/m length of leadline 45.45 45.45 45.45 45.45 45.45 网线直径/mm diameter of net twine 0.25 0.25 0.30 0.30 0.35 网片数量/片number of gillnets 10 10 10 7 10 1.3 数据收集
将网片按网目尺寸大小依次连接后，接连渔船实际生产网片进行作业。一般放网时间为04: 00~04: 30，起网时间为12: 30~13: 10，网片的平均浸泡时间约为8~9 h。一共完成了6网次捕捞试验。起网后按照网目尺寸摘取渔获，进行种类鉴定，然后测量生物学参数。
1.4 数据分析
1.4.1 SELECT模型的基本原理
假定cij为li体长的金线鱼被网目尺寸为mj的刺网捕获的数量，则：
$$ c_{i j}=q_i x_i \lambda_i S_{i j} $$ (1) 这里λi为li体长的金线鱼接触网具的数量；Sij为网目尺寸为mj的刺网对li体长的金线鱼的选择性；qi为渔具系数；xi为捕捞努力量。将pi定义为相对作业强度，而pi=qixi，式(1)表示为：
$$ c_{i j}=p_i x_i \lambda_i S_{i j} $$ (2) 其中$\sum\limits_{i=1}^k p_i=1$，k为所用网目总数。
根据几何相似假设，网目尺寸为mj的刺网对体长为li的金线鱼的选择性可表示如下：
$$ S_{i j}=s\left(l_{i j}\right) $$ (3) 将式(3)代入式(2)得：
$$ c_{i j}=p_i \lambda s\left(l_{i j}\right) $$ (4) 该研究用分别用Normal、Gama和Bi-normal模型计算刺网对金线鱼的选择率s(lij)，计算公式分别为：
$$ \text { Normal: } s\left(l_{i j}\right)=\exp \left[-\frac{\left(l_{i j}-k \cdot m_j\right)^2}{2 \sigma^2}\right] $$ (5) 式中待估参数为k和σ。
$$ \begin{aligned} & \;\;\;\text { Gama: } s\left(l_{i j}\right)=\left(\frac{l_{i j}}{(\alpha-1) \cdot k \cdot m_j}\right)^{\alpha-1} \exp (\alpha-1- \\ & \left.\frac{l_{i j}}{k \cdot m_j}\right) \end{aligned} $$ (6) 式中待估参数为α和k。
$$ \begin{aligned} & \;\;\;\text { Bi-normal: } s\left(l_{i j}\right)=\exp \left[-\frac{\left(l_{i j}-k_1 \cdot m_j\right)^2}{2 k_2^2 \cdot m_j^2}\right]+ \\ & \operatorname{cexp}\left[-\frac{\left(l_{i j}-k_3 \cdot m_j\right)^2}{2 k_4^2 \cdot m_i^2}\right] \end{aligned} $$ (7) 式中待估参数为k1, k2, k3, k4和c。
假设Cj为li体长的金线鱼被刺网捕获的总数，则：
$$ C_j=\sum\limits_{i=1}^k c_{i j} $$ (8) li体长的金线鱼被各网目尺寸c1j, ..., ckj捕获的概率可以用多项分布描述如下：
$$ P_j=\frac{C_{j}!}{\prod\limits_{i=1}^k c_{i j}!} \prod\limits_{i=1}^k \varphi_{i j}^{c_{i j}} $$ (9) 这里φij为li体长的金线鱼被网目尺寸为mj的刺网捕获的概率，其计算方程如下：
$$ \varphi_{i j}=c_{i j} / C_j=c_{i j} / \sum\limits_{i=1}^k c_{i j} $$ (10) 将式(9)应用于式(8)得到总的渔获概率为：
$$ P=\prod\limits_{j=1}^n P_j=\prod\limits_{j=1}^n\left(\frac{C_{j}!}{\prod\limits_{i=1}^n c_{i j}!} \prod\limits_{i=1}^k \varphi_{i j}^{c_{i j}}\right) $$ (11) 这里n为体长组的数量。将式(4)代入式(9)，可得模型估计的渔获概率为：
$$ \begin{aligned} & \;\;\;\varphi\left(l_{i j}\right)=p_i \lambda_i s\left(l_{i j}\right) / \sum\limits_{i=1}^k p_i \lambda_j s\left(l_{i j}\right)=p_i s\left(l_{i j}\right) / \sum\limits_{i=1}^k p_i \\ & s\left(l_{i j}\right) \end{aligned} $$ (12) 选择性参数和相对作业强度pi可以通过极大似然法进行估算，其似然方程如下：
$$ L=\prod\limits_{j=1}^n\left\{\frac{C_{j}!}{\prod\limits_{i=1}^k c_{i j}!} \prod\limits_{i=1}^k\left[p_i s\left(l_{i j}\right) / \sum\limits_{i=1}^k p_i s\left(l_{i j}\right)\right]^{c_{i j}}\right\} $$ (13) 在实际计算中，需要最大化对数似然函数，将常数项去除简化如下：
$$ \log _{\mathrm{e}} L=\sum\limits_{j=1}^n \sum\limits_{i=1}^k\left[c_{i j}\left(p_i s\left(l_{i j}\right) / \sum\limits_{i=1}^k p_i s\left(l_{i j}\right)\right)\right] $$ (14) 根据pi建立2个模型：1)等分隔模型(the equal split model)。假设所有刺网对康氏马鲛的捕捞概率相同，pi用各网目尺寸的实际捕捞努力量(实验中的网片数量)代替；2)估计分隔模型(the estimated split model)。pi由模型估计而得。
式(14)的求解用Excel 2010中的“规划求解”功能来实现[11, 19-20]。
1.4.2 模型优劣的判定
用赤池信息指数(Akaike′s Information Criterion，AIC)判断各模型的拟合度优劣，AIC的计算公式为：
$$ \mathrm{AIC}=-2 \mathrm{MLL}+2(K-1) $$ (15) 式中MLL为模型的最大对数尤度，K为待估参数的数量[21]。
2. 结果
2.1 渔获概况
试验共捕获目标种类金线鱼185尾，31.253 kg。40 mm刺网捕获金线鱼36尾(占19.46%)，45 mm刺网捕获金线鱼14尾(占7.57%)，50 mm刺网捕获金线鱼12尾(占6.49%)，55 mm刺网捕获金线鱼57尾(占36.22%)，60 mm刺网捕获金线鱼56尾(占30.27%)。金线鱼的体长分布见图 1。总体上，金线鱼体长分布呈先增大后减小的单峰分布趋势, 40 mm刺网捕捞的金线鱼众数体长组为171~180 mm，45 mm、50 mm刺网捕获的金线鱼众数体长组为191~200 mm，55 mm、60 mm刺网捕获的金线鱼众数体长组为201~210 mm(图 1)。
![]()
图 1 各网目尺寸捕捞的金线鱼体长分布Figure 1. Length distribution of N. virgatus for each mesh size gillnets2.2 选择性参数
Normal、Gama和Bi-normal模型估算的最大对数尤度值(MLL)、参数个数和AIC值见表 2。用等分隔模型估算的MLL绝对值比估计分隔模型的大；估计分隔模型的待参数个数比等分隔模型的多。同一种模型中，估计分隔模型的AIC值均小于等分隔模型。在所有模型中，Gama的估计分隔模型AIC值最小(466.55)，将其作为最佳拟合模型(以下简称最佳模型)。
表 2 根据估算AIC值判断各模型的拟合度优劣Table 2. Model selection based on AIC value for each model模型model 等分隔equal split model 估计分隔estimated split model MLL 参数个数number of parameters AIC MLL 参数个数number of parameters AIC normal -270.61 2 543.21 -227.39 7 466.79 Gama -276.14 2 554.29 -227.28 7 466.55a Bi-normal -272.37 5 552.74 -226.86 10 471.71 注：MLL. 模型的最大对数尤度值；a. AIC最小值
Note：MLL. maximum logarithmic value; a. minimum AIC value最佳模型估算的各项参数值及其标准差见表 3。模型残差值小于其自由度(P>0.05)，表明模型不存在拟合度缺失。刺网对金线鱼的相对作业强度(Pi)大小顺序依次为40 mm>60 mm>55 mm>45 mm>50 mm。最佳模型估算的相对作业强度与实际捕捞努力量(网片数量)的比较见图 2。40 mm、45 mm和50 mm刺网的相对作业强度与捕捞努力量差异较大。50 mm刺网的相对作业强度最小。各网目尺寸刺网拟合的残差值分布见图 3。40 mm、45 mm、50 mm、55 mm和60 mm刺网对金线鱼的众数体长理论值分别为146.27 mm、164.55 mm、182.84 mm、201.12 mm和219.40 mm。最佳模型拟合的选择性曲线见图 4。
表 3 最佳模型的参数估算值Table 3. Estimated parameters for the best fit model参数
parameter估计值
estimated value标准差
standard errora 53.57 2.562 2 k 0.07 0.001 5 p1 0.48 0.134 4 p2 0.07 0.009 0 p3 0.04 0.002 3 p4 0.20 0.046 0 p5 0.21 0.095 4 模型残差Model deviance 32.62 自由度df 38 P 0.72 注：p1、p2、p3、p4和p5分别代表网目尺寸为40 mm、45 mm、50 mm、55 mm和60mm的刺网对金线鱼的相对作业强度
Note：p1，p2，p3，p4 and p5 indicate relative operating intensities with gillnets of 40 mm，45 mm，50 mm and 60 mm.![]()
图 2 最佳模型估算的相对作业强度与捕捞努力量的比较Figure 2. Comparison between relative fishing intensity from the best fit model and relative fishing effort![]()
图 3 最佳模型拟合的各网目尺寸残差值Figure 3. Plots of residual deviance of gillnet of each mesh size in the best fit model2.3 最小网目尺寸的探讨
根据相关报道[22]，该研究将南海金线鱼的开捕规格(minimum landing size，MLS)定为150 mm。结合最佳模型选择性曲线，40 mm、45 mm、50 mm、55 mm和60 mm刺网对150 mm金线鱼的选择率分别为98.39%、80.94%、39.30%、13.70%和3.87%(图 4)。与50 mm刺网相比，55 mm刺网对150 mm金线鱼的选择率减少了25.6%。因此，该研究认为将金线鱼刺网最小网目尺寸定为55 mm，更加有利于保护渔业资源。
![]()
图 4 最佳模型拟合的选择性曲线Figure 4. Selectivity curves of gillnet of each mesh size from the best fit model3. 讨论
南海金线鱼流刺网属漂流单片刺网，渔具主尺度为36.97 m×4.80 m，主要渔获种类有金线鱼、带鱼(Trichiurus haumela)、长尾大眼鲷(Priacanthus tayenus)等。笔者参考该金线鱼流刺网的主尺度，制作了5组网目尺寸刺网共47片，进行了选择性试验。虽然各网目尺寸刺网的网片数量并不完全一致，但用SELECT模型进行拟合，估算出了刺网对金线鱼的选择性参数。由此可见，SELECT模型在刺网选择性参数估算中有重要作用。目前，在最佳选择性模型的判定中存在2种方法：1)比较模型残差值，最小者为最佳[11, 15]；2)比较AIC的大小，最小者为最佳[21]。由于模型间的估算参数数量不相同，即模型间的自由度存在差异，所以用AIC值作为评价和选择最佳拟合模型的标准更为合理。因为AIC值的计算公式包括了模型待估参数的个数。
南海金线鱼作业方式除流刺网外，还包括底拖网[1]。杨吝等[23]分析了拖网方目网囊对南海金线鱼的选择性，根据其研究结果，金线鱼50%选择叉长(L0.5)与方目网囊网目尺寸(m)存在如下关系：L0.5=21.85+1.68m (R=0.999 7)。将当时金线鱼的开捕规格120 mm(叉长)作为L0.5，可计算得方目网囊网目尺寸为58.42 mm。该网目尺寸比此研究建议的刺网最小网目尺寸55 mm略大。首先，拖网与刺网的捕捞原理有本质的区别。拖网是主动型渔具，遭遇网具的鱼类会本能产生逃逸行为，直至疲惫而被网囊捕获[24]。当金线鱼需要从拖网网囊的网目中逃逸时，逃逸能力已大为减弱。刺网是被动型渔具，以网目刺挂或网衣缠络进行作业[25]。当鱼体一旦发现刺网的存在，则会竭尽全力进行逃逸。拖网在作业过程中，由于渔船拖曳和水体的作用，即使是方目网囊也会产生一定的变形。另外，在金线鱼的可捕规格上，他们用的是120 mm叉长(广东省旧标准)；该研究则参考陈丕茂[22]的金线鱼开捕规格，为150 mm体长。两者存在一定的差异。
张鹏等[5]通过分析渔获物的多样性指数、相似性指数和ABC曲线(abundance biomass comparison curve)，认为当金线鱼刺网网目尺寸小于50 mm时对渔获生物群落的干扰较大。另外，农业部2014年发布的渔具管理通告中规定南海区流刺网最小网目尺寸也是50 mm。该研究在SELECT模型的架构下，重点分析刺网网目尺寸对金线鱼的选择率。根据各刺网对150 mm(MLS)金线鱼的选择率，该研究认为将50 mm作为南海金线鱼刺网的最小网目尺寸是不够的。因为网目尺寸为50 mm的刺网对体长为150 mm的金线鱼选择率高达39.30%，这意味着很大比例体长＜150 mm的金线鱼会被捕获，对金线鱼补充群体的损伤较大。当网目尺寸为55 mm时，刺网对体长为150 mm的金线鱼选择率为13.70%。虽然60 mm的刺网对体长为150 mm的金线鱼选择率更低，但考虑到网目尺寸过大可能会造成其他种类渔获量的下降，损害渔民的经济利益。因此，该研究建议将南海金线鱼流刺网最小网目尺寸暂定为55 mm。该研究仅从刺网对目标种类金线鱼的选择性进行分析和探讨，建议今后进行选择性的后续研究时，将南海金线鱼刺网对其副渔获种类的选择性作深入分析，为更科学、更合理地制定最小网目尺寸提供参考。
-
![]()
图 5 4个时间段网口沉降与闭合速度
Figure 5. Sinking and closing speed of net mouth at four time intervals
-
[1] 杨吝, 卢伙胜, 吴壮, 等. 南海区海洋渔具渔法[M]. 广州: 广东科技出版社, 2002: 164-168. [2] 张鹏, 杨吝, 张旭丰, 等. 南海金枪鱼和鸢乌贼资源开发现状及前景[J]. 南方水产, 2010, 6(1): 68-73. doi: 10.3969/j.issn.1673-2227.2010.01.012 [3] 晏磊, 张鹏, 杨吝, 等. 2011年春季南海中南部海域灯光罩网渔业渔获组成的初步分析[J]. 南方水产科学, 2014, 10(3): 97-103. doi: 10.3969/j.issn.2095-0780.2014.03.015 [4] 张鹏, 曾晓光, 杨吝, 等. 南海区大型罩网渔场渔期和渔获组成分析[J]. 南方水产科学, 2013, 9(3): 74-79. doi: 10.3969/j.issn.2095-0780.2013.03.012 [5] 邱永松, 张鹏. 南海大洋性渔业资源开发利用对策建议[C]. 热带海洋科学学术研讨会暨第八届广东海洋湖沼学会、第七届广东海洋学会会员代表大会论文及摘要汇编. 广州: 广东省科学技术协会科技交流部, 2013: 199-203. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-GDKL201305001026.htm [6] 杨吝, 张旭丰, 张鹏, 等. 南海区海洋小型渔具渔法[M]. 广州: 广东科技出版社, 2007: 103-115. [7] 杨吝, 张旭丰, 谭永光, 等. 南海北部灯光罩网渔获组成及其对渔业资源的影响[J]. 南方水产, 2009, 5(4): 41-46. doi: 10.3969/j.issn.1673-2227.2009.04.008 [8] 邹建伟, 陈立峰, 林蒋进. 南海外海灯光罩网主要渔场分布及变动研究——基于广西渔船的生产监测统计[J]. 南方水产科学, 2014, 10(4): 78-84. doi: 10.3969/j.issn.2095-0780.2014.04.013 [9] 颜云榕, 冯波, 卢伙胜. 中、西沙海域2种灯光作业渔船的捕捞特性及其技术效率分析[J]. 南方水产, 2009, 5(6): 59-64. doi: 10.3969/j.issn.1673-2227.2009.06.011 [10] 冯波, 许永雄, 卢伙胜. 南沙北部灯光罩网与金枪鱼延绳钓联合探捕[J]. 广东海洋大学学报, 2012, 32(4): 54-58. https://xueshu.baidu.com/usercenter/paper/show?paperid=42230c90c74c793caed758cd81c178fc [11] 杨权, 李永振, 张鹏, 等. 基于灯光罩网法的南海鸢乌贼声学评估技术研究[J]. 水产学报, 2013, 37(7): 1032-1039. doi: 10.3724/SP.J.1231.2013.38513 [12] 晏磊, 张鹏, 杨吝, 等. 南海灯光罩网沉降性能研究[J]. 上海海洋大学学报, 2014, 23(1): 146-153. https://xueshu.baidu.com/usercenter/paper/show?paperid=7c3cde045035a7ed323dc0ccfb4eb144&site=xueshu_se&hitarticle=1 [13] 冯维山. 围网下纲沉降特性试验研究[J]. 大连水产学院学报, 1990, 5(3): 37-43. https://xueshu.baidu.com/usercenter/paper/show?paperid=c20be56bccf9b5a4fdfab7eca99d5b04&site=xueshu_se&hitarticle=1 [14] MISUND O, DICKSON W, BELTESTAD A. Optimization of purse seines by large-meshed sections and low lead weight. Theoretical considerations, sinking speed measurements and fishing trials[J]. Fish Res, 1992, 14(4): 305-317. doi: 10.1016/0165-7836(92)90039-V
[15] 冯维山. 围网下纲提升特性研究[J]. 大连水产学院学报, 1993, 8(1): 29-36. https://xueshu.baidu.com/usercenter/paper/show?paperid=25f890fd8bc6b390b20042f81417a5c6&site=xueshu_se [16] SUK J K, JEONG S P. An analysis on the sinking characteristics of model purse seine by different netting material[J]. Kor Soc Fish Tech, 1995, 31(4): 372-379.
[17] SUK J K, JEONG S P. An analysis of sinking resistance for purse seine[J]. Kor Soc Fish Tech, 1998, 34(3): 275-234.
[18] KIM Y H. Geometry of the model purse seine in relation to enclosed volume during hauling operation[J]. Fish Aquat Sci, 2000, 3(2): 156-162. https://www.semanticscholar.org/paper/Geometry-of-the-Model-Purse-Seine-in-Relation-to-Yong-Hae/90875fbfcc024cfe61178f0c75a33f86916920e4
[19] HYUN Y K, CHUN W L, JONG K S, et al. Dynamic simulation of the behavior of purse seine gear and sea-trial verification[J]. Fish Res, 2007, 88(1/2/3): 109-119. doi: 10.1016/j.fishres.2007.08.007
[20] 王春雷. 中西太平洋1664.5m×394.3m金枪鱼围网沉降性能研究[D]. 上海: 上海海洋大学, 2008. 10.7666/d.y1660028 [21] YONG H K, MYEONG C P. The simulation of the geometry of a tuna purse seine under current and drift of purse seiner[J]. Ocean Eng, 2009, 36(14): 1080-1088. doi: 10.1016/j.oceaneng.2009.06.011
[22] HOSSEINI S A, LEE C W, KIM H S, et al. The sinking performance of the tuna purse seine gear with large-meshed panels using numerical method[J]. Fish Sci, 2011, 77(4): 503-520. doi: 10.1007/s12562-011-0371-6
[23] 兰光查. 基于模型试验的金枪鱼围网沉降性[D]. 上海: 上海海洋大学, 2011. [24] 许柳雄, 王敏法, 叶旭昌, 等. 金枪鱼围网沉降特性[J]. 中国水产科学, 2011, 18(5): 1161-1169. doi: 10.3724/SP.J.1118.2011.01161 [25] 许柳雄, 兰光查, 叶旭昌, 等. 下纲重量和放网速度对金枪鱼围网下纲沉降速度的影响[J]. 水产学报, 2011, 35(10): 1563-1569. doi: 10.3724/SP.J.1231.2011.17228 [26] 周成, 许柳雄, 张新峰, 等. 金枪鱼围网沉降性能影响因子的多元回归分析[J]. 中国水产科学, 2013, 20(3): 672-681. http://www.fishscichina.com/zgsckx/article/abstract/5178 [27] 唐浩, 许柳雄, 周成, 等. 基于GAM模型研究金枪鱼围网沉降性能影响因素[J]. 水产学报, 2013, 37(6): 944-950. doi: 10.3724/SP.J.1231.2013.38336 [28] 唐浩, 许柳雄, 王学昉, 等. 金枪鱼围网模型试验结果与海上实测的比较评估[J]. 中国水产科学, 2013, 20(4): 884- 892. doi: 10.3724/SP.J.1118.2013.00884 [29] 李灵智, 黄洪亮, 陈帅, 等. 基于静水池模型试验的金枪鱼围网沉降性能研究[J]. 中国海洋大学学报, 2015, 45(3): 48-53. doi: 10.16441/j.cnki.hdxb.20130275 [30] 徐国强, 许柳雄, 周成, 等. 基于海上实测的金枪鱼围网下纲沉降及提升性能[J]. 海洋渔业, 2015, 37(2): 171-178. https://www.doc88.com/p-3827777355463.html [31] 袁军亭. 网片的三维力学模型研究及应用[D]. 上海: 上海海洋大学, 2007. https://xueshu.baidu.com/usercenter/paper/show?paperid=455aa289a29ea0e71f45ac9155cdb80b&site=xueshu_se&hitarticle=1 [32] 黄小华, 郭根喜, 胡昱, 等. 圆形网衣在水流作用下的运动变形特性[J]. 中国水产科学, 2010, 17(2): 312-319. https://xueshu.baidu.com/usercenter/paper/show?paperid=69cefe25fc788c59234bc177cb8209cd&site=xueshu_se&hitarticle=1 [33] 赵云鹏. 深水重力式网箱水动力特性数值模拟研究[D]. 大连: 大连理工大学, 2007. 10.7666/d.y1205374 [34] 张俊, 陈作志, 陈国宝, 等. 南海鸢乌贼水声学测量和评估相关技术研究[J]. 南方水产科学, 2014, 10(6): 1-11. doi: 10.3969/j.issn.2095-0780.2014.06.001 -
期刊类型引用(4)
1. 朱轩仪，郑晓婷，邢逸夫，黄建华，董宏标，张家松. 三丁酸甘油酯提高凡纳滨对虾鳃组织抗周期性高温胁迫能力的研究. 南方水产科学. 2024(03): 66-75 . 
本站查看
2. 刘蕊，张云岭，张秀文，牛天，宋凯，齐遵利. 刺参良种健康苗种繁育技术. 水产养殖. 2024(07): 59-61 . 百度学术
3. 侯润，张云岭，张秀文，安鑫龙，赵祺，韩宗奇，牛天，齐遵利. 刺参工厂化苗种繁育与生态保苗技术. 河北渔业. 2023(03): 8-13 . 百度学术
4. 赵斌，胡炜，李成林，韩莎. 温度和盐度对紫刺参(Apostichopus japonicus Selenta)稚参存活、生长和着色的影响. 海洋与湖沼. 2018(03): 700-706 . 百度学术
其他类型引用(0)
下载:
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 4
粤公网安备 44010502001741号
