Model test of hydrodynamic characteristics of two types of vertical cambered slotted otter boards
-
摘要:
为通过调节导流翼偏角优化网板的水动力学性能,利用水槽模型试验测得2种立式曲面缝翼式网板各3种导流翼偏角状态下的升力系数(CL)、阻力系数(CD)和升阻比(K)。结果表明:1)对单缝翼立式曲面网板,冲角为20°~35°时,随着导流翼偏角的增大,网板升力系数和阻力系数均呈下降趋势。该冲角范围内,导流翼偏角为35°的网板(D1)具有较佳的水动力学性能;2)对双缝翼立式曲面V型网板,冲角为25°~35°时,前导流翼偏角为20°、中导流翼偏角为25°的网板(S3)具有较佳的水动力学性能。根据试验结果,建议D1网板最佳工作冲角范围为15°~30°,此时CL>1.2且K>2.0;S3网板最佳工作冲角范围为20°~30°,此时CL>0.8且K>3.0。导流翼偏角增加时网板升力系数的临界冲角有增加的趋势,合理调节导流翼偏角可以达到优化网板水动力学性能的目的。
Abstract:To study the effect of flow deflector angle on the hydrodynamic performance of otter board, a flume model experiment was conducted to measure the lift coefficient (CL), drag coefficient (CD) and lift to drag ratio (K) of two flow deflector vertical cambered otter boards, each with three kinds of flow deflector angle. The experimental results show that: 1) For the single flow deflector vertical cambered otter board, when the angle of attack was between 20°~35°, the CL and CD values showed a downtrend with increase of flow deflector angle. In this case the otter board D1 (flow deflector angle was 35°) showed better hydrodynamic performance. 2) For the double flow deflector vertical cambered otter board, when the angle of attack was between 25°~35°, the otter board S3 (the front flow deflector angle was 20° and the middle flow deflector angle was 25°) showed better hydrodynamic performance. It is suggested that the best working scope of angle of attack of otter board D1 was between 15°~30°, in that case, CL>1.2 and K>2.0;the best working scope of angle of attack of otter board S3 was between 20°~30°, in that case, CL>0.8 and K>3.0. The critical angle of attack of lift coefficient increased with increase of flow deflector angle. Properly regulating flow deflector angle could optimize the hydrodynamic performance of otter board.
-
Keywords:
- otter board /
- flow deflector /
- hydrodynamic characteristics /
- model test
-
在对虾养殖过程中,由于人工投饵和施肥,随着养殖时间的延长,水体中的化学需氧量(COD)、氨氮(NH3-N)和亚硝酸氮(NO2-N)含量不断增加,导致水质恶化,抑制了对虾的生长,甚至引发疾病和造成死亡[1-3]。枯草芽孢杆菌(Bacillus substilis)没有毒性,不会对生物体产生危害[4],且能利用水体中的有机质,抑制NH3-N和NO2-N的产生[5]。目前,已有学者研究利用枯草芽孢杆菌及其提取物作为添加剂提高对虾抗病力、成活率及饲料利用[6-7],但利用枯草芽孢杆菌改善凡纳滨对虾(Penaeus vannamei)幼体培育环境水质、提高对虾免疫力的研究未见报道。因此,该试验进行枯草芽孢杆菌改善水质,增强凡纳滨对虾幼体抗病力的研究,以期为对虾的生态育苗提供理论依据。
1. 材料与方法
1.1 试验设计
试验设1个对照组(编号为A0)和5个试验组(依浓度递增顺序编为A1、A2…A5),试验组枯草芽孢杆菌投放量分别为1.25×102、1.25×103、1.25×104、1.25×105和1.25×106 cfu·mL-1,每组设2个平行组。试验过程中开增氧机,第5天再投放1次。试验水体为0.1 m3的水族箱放养凡纳滨对虾P6期幼体(以下简称对虾)300尾,试验期间不换水,每隔1 d测1次水质指标。20 d后检测相关酶的活性、成活率和增重率。
1.2 试验用对虾和海水
试验用对虾和海水均由湛江中联养殖有限公司提供。海水经沙滤处理。试验期间,投喂博尚牌顶好虾片,每天投喂4次(8:00,12:00,17:00和22:00),每次投喂0.5 g。
1.3 菌种来源
枯草芽孢杆菌(固态,1.25×1012 cfu·g-1)由广东海洋大学微生物实验室提供。
1.4 水质测定的方法
NH3-N用纳氏试剂法测定;NO2-N采用重氮-偶氮光度法测定;COD用碱性高锰酸钾法测定(CODMn)[8]。
1.5 成活率与增重率
对虾体质量使用50尾对虾进行测量,成活率直接计数。
成活率(%) =收获时存活数目×100/初始放养数目
增重率(%) = (收获时50尾对虾的体质量-初始放养时50尾对虾的体质量) ×100/初始放养时50尾对虾的体质量
1.6 酶活力的测定
每组取50尾对虾,按1 : 5加入对虾生理盐水[9],置于冰上匀浆,匀浆液0 ℃下,10 000 r·min-1离心10 min,取上清液进行酶活性测定。其中碱性磷酸酶(AKP)、过氧化物酶(POD)、溶菌活力和超氧化物歧化酶(SOD)活力用南京建成生物工程研究所生产的试剂盒测定。酚氧化酶(PO)活力参照以L-dopa为底物比色的方法测定[10]。抗菌活力测定以大肠杆菌为底物,用0.1 mol·L-1(pH 6)的KH2PO4-K2HPO4缓冲液配成OD570=0.4的大肠杆菌悬浮液,按王雷等[9]的方法测定。
1.7 统计分析
用SPSS 13.0对数据进行方差分析和Duncan多重比较。
2. 结果
2.1 水质分析结果
2.1.1 水体中NH3-N的变化
引入枯草芽孢杆菌能降低水体中NH3-N的含量。在投放枯草芽孢杆菌后的第3天,试验组的NH3-N降到最低;从第3天到第7天各组均有所上升;第7天后试验组NH3-N开始下降。A3组的NH3-N浓度平均值比对照组降低了59.70%。随机抽取第3、7和13天的数据进行方差分析,结果均显示对照组与试验组差异极显著(P < 0.01),但各试验组间差异不显著(P>0.05)(图 1-a)。
2.1.2 水体中NO2-N的变化
引入枯草芽孢杆菌能抑制水体中NO2-N的含量。在试验期间,A3组NO2-N≤0.011 mg·L-1且保持较稳定的状态,该组的NO2-N浓度平均值比对照组低88.64%;对照组NO2-N逐渐上升;其余各组在前7 d NO2-N都维持在较低水平,第7天后NO2-N逐渐上升,但始终低于对照组。对第3、7和13天数据进行方差分析,结果显示,第3天各组间无显著差异(P>0.05);第7天对照组NO2-N含量显著(P < 0.05)高于试验组,各试验组间差异不显著(P>0.05);第13天对照组NO2-N含量显著高于试验组(P < 0.05)(图 1-b)。
2.1.3 水体中CODMn的变化
枯草芽孢杆菌能有效降解水体中的有机质。在投放枯草芽孢杆菌后的第3天,试验组中的CODMn降到最低;从第3天到第7天各试验组均有所上升;第7天后试验组CODMn下降。在试验期间试验组CODMn一直低于对照组;对照组CODMn随着养殖时间延长而逐渐升高。A3组的CODMn平均值比对照组降低了65.30%。取第3、7和13天的数据进行方差分析,结果均显示对照组与试验组差异极显著(P < 0.01),但各试验组间差异不显著(P>0.05)(图 1-c)。
2.2 对虾免疫指标的测定
2.2.1 AKP活力测定结果
不同枯草芽孢杆菌投放浓度对对虾AKP活力的影响见图 2-a。枯草芽孢杆菌对AKP活力影响显著(P < 0.05);投放浓度在1.25×104 cfu·mL-1时AKP活力最大,达31.65 U·gprot-1,比对照组提高3.67倍。Duncan多重比较结果表明,AKP活力最大时的枯草芽孢杆菌初始投放浓度为1.25×104 cfu·mL-1。
![]() 图 2 AKP活力(a)、SOD活力(b)、PO活力(c)、POD活力(d)、抗菌活力(e)、溶菌活力(f)、对虾的成活率(g)和增重率(h)柱形图上标的字母差异是Duncan多重比较的结果,不同字母表示差异显著。Figure 2. Activities of AKP(a), SOD(b), PO(c), POD(d), antibacteria(e), bacteriolysis(f), survival rate of P.vannamei(g)and weight gain (h)of P.vannameiDifferent letters above columns mean significant difference, which is a result from Duncan multiple comparison.
图 2 AKP活力(a)、SOD活力(b)、PO活力(c)、POD活力(d)、抗菌活力(e)、溶菌活力(f)、对虾的成活率(g)和增重率(h)柱形图上标的字母差异是Duncan多重比较的结果,不同字母表示差异显著。Figure 2. Activities of AKP(a), SOD(b), PO(c), POD(d), antibacteria(e), bacteriolysis(f), survival rate of P.vannamei(g)and weight gain (h)of P.vannameiDifferent letters above columns mean significant difference, which is a result from Duncan multiple comparison.2.2.2 SOD活力测定结果
不同枯草芽孢杆菌投放浓度对对虾SOD活力的影响见图 2-b。枯草芽孢杆菌对SOD活力影响显著(P < 0.05);投放浓度在1.25×104 cfu·mL-1时SOD活力最大,达225.78 U·gprot-1,比对照组提高3.06倍。Duncan多重比较结果表明,SOD活力最大时的枯草芽孢杆菌初始投放浓度为1.25×104 cfu·mL-1。
2.2.3 PO活力测定结果
不同枯草芽孢杆菌投放浓度对对虾PO活力的影响见图 2-c。枯草芽孢杆菌对PO活力影响显著(P < 0.05);投放浓度在1.25×104 cfu·mL-1时PO活力最大,达3.00 U,比对照组提高了0.45倍。Duncan多重比较结果表明,PO活力最大时的枯草芽孢杆菌初始投放浓度为1.25×104~1.25×105 cfu·mL-1。
2.2.4 POD活力测定结果
不同枯草芽孢杆菌投放浓度对对虾POD活力的影响见图 2-d。枯草芽孢杆菌对POD活力影响显著(P < 0.05);投放浓度在1.25×104 cfu·mL-1时POD活力最大,达9.70 U·mg prot-1,比对照组提高1.64倍。Duncan多重比较结果表明,POD活力最大时的枯草芽孢杆菌初始投放浓度为1.25×104 cfu·mL-1。
2.2.5 抗菌活力测定结果
不同枯草芽孢杆菌投放浓度对对虾抗菌活力的影响见图 2-e。枯草芽孢杆菌对抗菌活力影响显著(P < 0.05);投放浓度在1.25×104 cfu·mL-1时抗菌活力最大,达0.35 U·mL-1,比对照组提高2.57倍。Duncan多重比较结果表明,抗菌活力最大时的枯草芽孢杆菌初始投放浓度为1.25×104 cfu·mL-1。
2.2.6 溶菌活力测定结果
不同枯草芽孢杆菌投放浓度对对虾溶菌活力的影响见图 2-f。枯草芽孢杆菌对溶菌活力影响极显著(P < 0.01);投放浓度在1.25×104 cfu·mL-1时溶菌活力最大,达219.04 U·mL-1,比对照组提高2.14倍。Duncan多重比较结果表明,溶菌活力最大时的枯草芽孢杆菌初始投放浓度为1.25×104 cfu·mL-1。
2.3 成活率与增重率
2.3.1 成活率
不同浓度枯草芽孢杆菌对对虾成活率的影响见图 2-g。枯草芽孢杆菌对对虾成活率影响显著(P < 0.05);当投放浓度为1.25×104 cfu·mL-1时,成活率最高,达到97.83%,比对照组增加了10.00%。Duncan多重比较结果表明,成活率最高时的枯草芽孢杆菌使用量为1.25×104 cfu·mL-1。
2.3.2 增重率
不同浓度枯草芽孢杆菌对对虾增重率的影响见图 2-h。不同浓度梯度枯草芽孢杆菌对对虾增重率影响极显著(P < 0.01);当投放浓度达到1.25×104 cfu·mL-1时,增重率最高,达到432.31%,是对照组的2.44倍。Duncan多重比较结果表明,增重率最高时的枯草芽孢杆菌使用量为1.25×104 cfu·mL-1。
3. 讨论
3.1 枯草芽孢杆菌对水质的改善作用
枯草芽孢杆菌在水中增殖后产生的许多胞外酶能把养殖水体和底泥中的淀粉、蛋白质和脂肪等有机质分解,从而达到降低养殖水体富营养化和减少底泥生成的作用。在分解过程中,有机物一部分转化为细菌胞体物质,而大部分被转化为细菌生命活动过程中所需能量,同时氨气、氮气和二氧化碳等代谢终产物从水中弥散到空气中。通过这种方法,养殖水体中的NH3-N和NO2-N可显著减少[11]。枯草芽孢杆菌能迅速而有效地降低水中NO2-N的含量并显著降低水体的COD[12];有研究发现使用枯草芽孢杆菌后NH3-N最大降解值出现在使用后的第3~4天,NO2-N的最大降解值出现在使用后的第3天[13]。这与此试验的研究结果一致,有可能是由枯草芽孢杆菌的生长周期决定的。虽然枯草芽孢杆菌30 ℃时的世代时间为31 min,每24 h可分裂46次,增殖数为7.0×1013个。事实上由于种种客观条件的限制,细菌的指数分裂速度只能维持数小时,因而在液体培养中,细菌的浓度一般仅能达到每毫升108~109个左右[14-15]。由此试验的初始浓度,如果按照每天指数分裂3~4 h计算,枯草芽孢杆菌的浓度最大值应该出现在第3天。试验期间,试验组的COD、NH3-N和NO2-N含量均显著(P < 0.05)低于对照组;当枯草芽孢杆菌使用浓度为1.25×104 cfu·mL-1时,COD、NH3-N和NO2-N含量均值比对照组分别降低了65.30%、59.70%和88.64%。成活率比对照组提高了10%,增重率是对照组的2.44倍;这可能是由于NH3-N、NO2-N和有机物等对对虾的生长造成胁迫,而枯草芽孢杆菌能利用有机物降低水体中的NH3-N和NO2-N,进而提高对虾成活率与增重率。因此,适宜浓度的枯草芽孢杆菌能改善养殖水体的水质,促进对虾生长。
3.2 NH3-N与NO2-N对对虾免疫指标的影响
高浓度NH3-N和NO2-N对虾体有致死作用[16],即使在低于致死浓度的条件下对对虾生理功能(如氧消耗、氨排泄、ATPase活性及渗透压)也有显著影响[17]。甲壳类动物血液中的血蓝蛋白,其辅基是含铜的化合物,水体中的NO2-N进入虾类的血淋巴后,促使氧合血蓝蛋白转化为脱氧血蓝蛋白,导致血淋巴对氧的亲和性降低,从而降低了机体的输氧能力[18],因此会对机体产生毒害作用。已有研究表明,水体中NH3-N浓度过高会导致中国对虾(Penaeus chinesis)血清中PO、SOD和溶菌酶活力下降[19];NO2-N可降低日本对虾(P.japonicus)和罗氏沼虾(Macrobrachium rosenbergi)的抗病力水平、血细胞吞噬活力以及对细菌的清除效率[20];高浓度的NO2-N降低了凡纳滨对虾的血细胞数、SOD活力、PO活力、抗菌活力和溶菌活力[21]。此试验表明,在枯草芽孢杆菌使用浓度为1.25×104 cfu·mL-1时,养殖水体中COD、NH3-N和NO2-N含量均值比对照组分别降低了65.30%、59.70%和88.64%;凡纳滨对虾的AKP、POD、PO、SOD、抗菌和溶菌活力均显著(P < 0.05)提高,相对于对照组分别提高了3.67、1.64、0.45、3.06、2.57和1.14倍。因此,枯草芽孢杆菌可以通过降低水体中NH3-N和NO2-N浓度,进而提高免疫相关酶的活性,增强对虾抗病力。基于试验结果,在对虾育苗过程中枯草芽孢杆菌的建议使用浓度为1.25×104 cfu·mL-1。
-
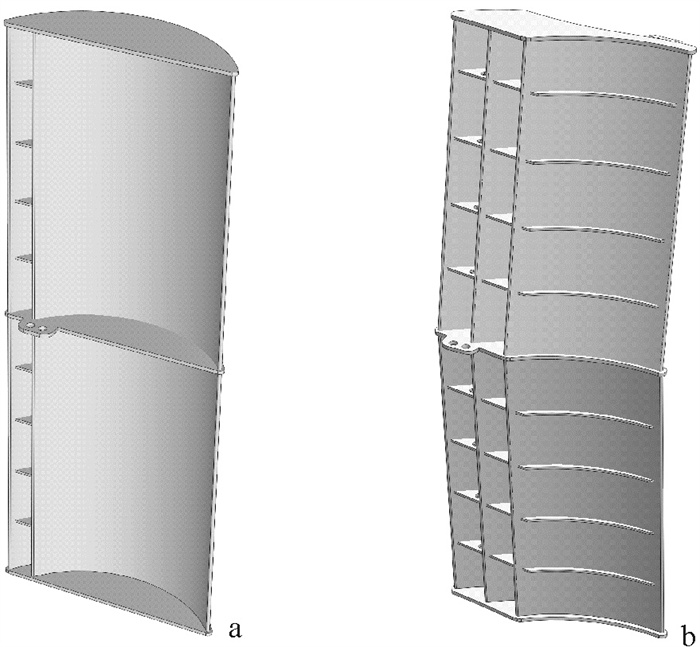
表 1 网板模型规格
Table 1 Specification of model otter board
型号
type编号
No.导流翼偏角
angle of flow deflector翼弦长/cm
wing chord length展弦比
aspect ratio面积/m2
sectional area单缝翼式single flow deflector D1 β=35° 9.3 2.7 0.024 D2 β=40° D3 β=45° 双缝翼式double flow deflector S1 θ=15°,γ=20° 9.1 2.9 0.024 S2 θ=20°,γ=20° S3 θ=20°,γ=25° 表 2 网板最大升力系数和最大升阻比
Table 2 Max lift coefficient and max lift to drag ratio of otter board
型号type 编号No. 最大升力系数CLmax 最大升阻比Kmax 单缝翼式single flow deflector D1 1.983 (α=35°) 2.389 (α=20°) D2 1.877 (α=40°) 2.262 (α=20°) D3 1.841 (α=40°) 2.530 (α=5°) 双缝翼式double flow deflector S1 1.369 (α=30°) 3.906 (α=15°) S2 1.398 (α=30°) 2.658 (α=20°) S3 1.630 (α=35°) 3.756 (α=25°) 表 3 不同工作冲角下水动力学性能比较
Table 3 Comparison of hydrodynamic performance at different angles of attack
工作冲角α
angle of attack编号
No.升力系数CL
lift coefficient阻力系数CD
drag coefficient升阻比K
lift to drag ratio15° D1 1.294 0.543 2.385 S3 0.660 0.231 2.854 20° D1 1.603 0.671 2.389 S3 0.954 0.310 3.081 25° D1 1.801 0.778 2.316 S3 1.321 0.352 3.756 30° D1 1.926 0.886 2.173 S3 1.568 0.498 3.149 35° D1 1.983 0.965 2.055 S3 1.630 0.663 2.457 注: 下划线表示本系列最大值
Note: The underline indicates the maximum of this type. -
[1] 郭根喜, 刘同渝, 黄小华, 等. 拖网网板动力学理论研究与实践[M]. 广州: 广东科技出版社, 2008: 160-211. [2] 张勋, 王明彦, 徐宝生. 拖网网板型式、结构与性能的研究与应用进展[J]. 中国水产科学, 2004, 11(z1): 107-113. doi: 10.3321/j.issn:1005-8737.2004.z1.022 [3] 徐宝生, 张勋, 郁岳峰, 等. 矩形V型曲面网板和V型网板生产性对比试验[J]. 海洋渔业, 2006, 28(1): 66-70. doi: 10.3969/j.issn.1004-2490.2006.01.012 [4] BROADHURST M K, STERLING D J, CULLIS B R. Effects of otter boards on catches of an Australian penaeid trawl[J]. Fish Res, 2012, 131/133: 67-75. doi: 10.1016/j.fishres.2012.07.015
[5] 徐宝生, 张勋, 王明彦. 单船拖网网板的现状及发展趋势[J]. 福建水产, 2010(1): 86-90. doi: 10.3969/j.issn.1006-5601.2010.01.022 [6] 陈雪忠, 黄锡昌. 渔具模型试验理论与方法[M]. 上海: 上海科学技术出版社, 2011: 388-425. https://www.zhangqiaokeyan.com/book-cn/081504720106.html [7] SALAA A, FARRANB J P, ANTONIJUAN J, et al. Performance and impact on the seabed of an existing-and an experimental-otterboard comparison between model testing and full-scale sea trials[J]. Fish Res, 2009, 100(2): 156-166. doi: 10.1016/j.fishres.2009.07.004
[8] PARK H H. A method for estimating the gear shape of a mid-water trawl[J]. Ocean Eng, 2007, 34(3/4): 470-478. doi: 10.1016/j.oceaneng.2006.03.001
[9] PRAT J, ANTONIJUAN J, FOLCH A, et al. A simplified model of the interaction of the trawl warps, the otterboards and netting drag[J]. Fish Res, 2008, 94(1): 109-117. doi: 10.1016/j.fishres.2008.07.007
[10] SUN X F, YIN Y, JIN Y C, et al. The modeling of single-boat, mid-water trawl systems for fishing simulation[J]. Fish Res, 2011, 109(1): 7-15. doi: 10.1016/j.fishres.2010.12.027
[11] 刘健, 黄洪亮, 陈帅, 等. 小展弦比立式曲面网板的水动力性能[J]. 水产学报, 2013, 37(11): 1742-1749. doi: 10.3724/SP.J.1231.2013.38768 [12] 刘健, 黄洪亮, 陈帅, 等. 两种立式曲面V型网板水动力性能的实验研究[J]. 水动力学研究与进展A辑, 2014, 29(2): 183-188. https://www.zhangqiaokeyan.com/academic-journal-cn_detail_thesis/02012118496950.html [13] 福田賢吾, 松田皎, 胡夫祥, 等. 複葉型オッターボードの流体特性に関する模型実験[J]. 日本水産學會誌, 1997, 63(2): 207-212. https://cir.nii.ac.jp/crid/1390001206412963712 [14] 福田賢吾, 胡夫祥, 東海正, 等. 複葉型オッターボードの流体特性に及ぼす湾曲板の縦横比および反り比の影響[J]. 日本水産學會誌, 1999, 65(5): 860-865. https://cir.nii.ac.jp/crid/1390001206413308800 [15] 福田賢吾, 胡夫祥, 東海正, 等. 湾曲板の揚抗力特性に及ぼす縦横比の影響[J]. 日本水産學會誌, 2000, 66(1): 97-103. https://cir.nii.ac.jp/crid/1390001206413835008 [16] 木下弘実, 熊沢泰生. 柔構造拡網装置(カイト)を用いたトロール漁具の開発[J]. 日本水産工学, 2011, 48(2): 89-98. https://cir.nii.ac.jp/crid/1390001205862502144 [17] 山崎慎太郎, 松下吉樹, 川島敏彦, 等. 伊勢湾底びき網漁業に用いられるオッターボードの性能評価と新型オッターボードの提案[J]. 日本水産學會誌, 2007, 73(2): 220-225. https://jglobal.jst.go.jp/detail?JGLOBAL_ID=200902213943575229 [18] 关长涛, 潘生弟. 大型拖网渔船网板性能的试验研究[J]. 海洋水产研究, 1998, 19(2): 93-100. https://d.wanfangdata.com.cn/periodical/Ch9QZXJpb2RpY2FsQ0hJTmV3UzIwMjQxMTA1MTcxMzA0Eg5RSzE5OTgwMDI3MTQwNhoIMXNsYnM5YzY%3D [19] 王明彦, 王锦浩, 张勋, 等. 立式V型曲面网板的水动力性能[J]. 水产学报, 2004, 28(3): 311-315. doi: 10.3321/j.issn:1000-0615.2004.03.016 [20] 张勋, 王锦浩, 王明彦, 等. 矩形V型曲面网板水动力性能的研究-Ⅰ: 导流板曲率与网板水动力性能的关系[J]. 中国水产科学, 2004, 11(z1): 5-8. https://www.nstl.gov.cn/paper_detail.html?id=f6b4a234a82ce86f90146a6b9925ecdd [21] 王锦浩, 张勋, 王明彦, 等. 矩形V型曲面网板水动力性能的研究-Ⅱ: 展弦比、缝口位置、缝口宽度对网板水动力性能的影响[J]. 中国水产科学, 2004, 11(z1): 9-13. doi: 10.3321/j.issn:1005-8737.2004.z1.003 [22] 李崇聪. V型网板水动力性能和数值模拟初步研究[D]. 青岛: 中国海洋大学, 2012. 10.7666/d.y2212328 -
期刊类型引用(32)
1. 章霞,王易帆,陈爽,李伟业,殷小龙,徐羡. 添加枯草芽孢杆菌和锁掷酵母对大黄鱼仔稚鱼育苗水处理效果的影响. 安徽农业科学. 2025(04): 63-66 .  百度学术
百度学术
2. 张晶晶,林煜,陈度煌,陈斌,薛凌展,樊海平. 水体投放枯草芽孢杆菌对不同习性鱼类肠道菌群和水质影响的研究. 渔业研究. 2024(02): 136-146 .  百度学术
百度学术
3. 邱月. 枯草芽孢杆菌在现代农业中的应用. 园艺与种苗. 2022(07): 81-85 .  百度学术
百度学术
4. 陈皓祥,邓益琴,程长洪,马红玲,郭志勋,冯娟. 养殖池塘14株芽孢杆菌的分离鉴定及抑菌效果. 热带生物学报. 2022(06): 605-613 .  百度学术
百度学术
5. 李咏梅,李腾飞,田相利,罗凯,王龙斌,张盛坤,魏聪,刘杨. 添加益生菌和PHBV对凡纳滨对虾养殖系统水质和对虾生长、非特异免疫指标的影响. 中国海洋大学学报(自然科学版). 2021(11): 22-31 .  百度学术
百度学术
6. 刘洋,宋志文,李凌志,徐爱玲. 微生态制剂-生物膜对虾养殖系统水质净化效果研究. 水生态学杂志. 2020(01): 92-99 .  百度学术
百度学术
7. 李淑翠. 益生菌在对虾养殖中的应用研究. 江西水产科技. 2020(06): 52-53 .  百度学术
百度学术
8. 辛美丽,吴海一,刘玮,吕芳,丁刚. 一株降解刺参残饵的芽孢杆菌分离、鉴定及施用效果. 海洋湖沼通报. 2019(06): 133-138 .  百度学术
百度学术
9. 郭正富,李军,杨小琴. 枯草芽孢杆菌对鲤鱼抗氧化性能和免疫性能的影响. 中国饲料. 2018(08): 75-79 .  百度学术
百度学术
10. 胡瑞萍,丁贤,李来好,李俊伟,伍文超,徐宁. 响应面法优化枯草芽孢杆菌NHS1产芽孢发酵培养. 生态学杂志. 2018(02): 605-612 .  百度学术
百度学术
11. 杨明容,陈再炜,曹岩,李小勇,江俊勇. 枯草芽孢杆菌对泥鳅养殖水体水质的影响. 江西水产科技. 2017(05): 3-6 .  百度学术
百度学术
12. 王苓,田相利,董双林,汪多. 两株芽孢杆菌对凡纳滨对虾生长和血清非特异性免疫指标的影响研究. 中国海洋大学学报(自然科学版). 2017(04): 14-21 .  百度学术
百度学术
13. 高肖微,齐遵利,张秀文. 饲料中添加地衣芽孢杆菌对鲤鱼生长性能及非特异性免疫功能的影响. 饲料工业. 2016(08): 16-19 .  百度学术
百度学术
14. 张连水,张慧霞,孟会贤,张君,李国信,张洪志. 微生态制剂的研究现状及前景. 河北渔业. 2016(02): 56-59+70 .  百度学术
百度学术
15. 董宏标,陈亮亮,冯震华,文国樑,段亚飞,李卓佳,张家松. 尼龙筛绢基质对对虾养殖水体细菌群落结构演替的影响. 南方水产科学. 2016(01): 17-22 .  本站查看
本站查看
16. 杨荣芳. 饲用枯草芽孢杆菌在水产养殖中的应用. 黑龙江畜牧兽医. 2015(23): 234-236 .  百度学术
百度学术
17. 董春光,杨爱国,孙秀俊,吴彪,刘志鸿,周丽青,侯丫. 枯草芽孢杆菌(Bacillus subtilis)在刺参养殖中的益生作用. 渔业科学进展. 2015(03): 109-115 .  百度学术
百度学术
18. 关洪斌,张森,唐清源,郝晗,林婧宇,余梦迪,仲萌萌,肖曼玉,李宇航,车军威,刘迪,王晓兰. 淡水养殖中有利于草金鱼生长且高效环保的养殖方法探究. 饲料研究. 2015(22): 38-44 .  百度学术
百度学术
19. 虞为,李卓佳,林黑着,陈利雄,朱李春,张燕娃,黄春阳,陈志红,黄忠,黄小林,杨育凯,李涛,朱长波. 对虾养殖池塘混养罗非鱼对底质有机负荷的作用. 中国渔业质量与标准. 2015(03): 8-12 .  百度学术
百度学术
20. 程远,黄凯,黄秀芸,钟灵香,武林华,黄清,唐丽宁. 饲料中添加枯草芽孢杆菌对吉富罗非鱼幼鱼生长性能、免疫力和抗氧化功能的影响. 动物营养学报. 2014(06): 1503-1512 .  百度学术
百度学术
21. 李桂英,孙艳,宋晓玲,黄倢,谢国驷. 饲料中添加潜在益生菌对凡纳滨对虾肠道消化酶活性和菌群组成的影响. 渔业科学进展. 2013(04): 84-90 .  百度学术
百度学术
22. 许合金,冯幼,刘定,陈子腾,许进奉. 枯草芽孢杆菌在对虾生产中的应用. 饲料博览. 2013(04): 40-42 .  百度学术
百度学术
23. 虞为,李卓佳,王丽花,张晓阳,曹煜成,文国樑,朱长波,马广智. 对虾单养和对虾-罗非鱼混养试验围隔水质动态及产出效果的对比. 中国渔业质量与标准. 2013(02): 89-97 .  百度学术
百度学术
24. 李卓佳,虞为,朱长波,文国樑,马广智. 对虾单养和对虾-罗非鱼混养试验围隔氮磷收支的研究. 安全与环境学报. 2012(04): 50-55 .  百度学术
百度学术
25. 丁贤,唐维可,张善夫,李卓佳,林黑着,杨铿. 芽孢杆菌对草鱼消化酶活性及血清生化指标的影响. 广东农业科学. 2012(17): 121-124 .  百度学术
百度学术
26. 王瑞旋,冯玉婷,冯娟,王江勇. 近江牡蛎Crassostrea hongkongensis体内细菌的周年变化及细菌产酶能力. 海洋环境科学. 2012(06): 851-854+866 .  百度学术
百度学术
27. 廉新慧,张高娜,刘凤芝,李春凤,谷巍. 枯草芽胞杆菌在动物生产中的应用. 畜牧与饲料科学. 2012(10): 23-24 .  百度学术
百度学术
28. 田功太,刘飞,段登选,杜兴华,张金路,陈述江,张明磊,王慧. EM菌对海参养殖水体主要污染物净化效果的研究. 山东农业大学学报(自然科学版). 2012(03): 381-386 .  百度学术
百度学术
29. 贺国龙,刘立鹤,张恒,刘军,谭斌,周晓辉. 不同加工工艺及保存方式对饲料中芽孢数量的影响. 武汉工业学院学报. 2012(02): 15-19 .  百度学术
百度学术
30. 虞为,李卓佳,朱长波,马广智. 我国对虾生态养殖的发展现状、存在问题与对策. 广东农业科学. 2011(17): 168-171 .  百度学术
百度学术
31. 冯东岳,钱冬. 2005~2009年凡纳滨对虾白斑综合征和桃拉综合征的流行情况分析. 南方水产科学. 2011(01): 78-83 .  本站查看
本站查看
32. 丁贤,李卓佳,于明超,王华朗,陈永青. 益生菌ZD02的分离及其在对虾集约化精养中的应用. 生态学杂志. 2010(12): 2419-2424 .  百度学术
百度学术
其他类型引用(43)




 下载:
下载:






 粤公网安备 44010502001741号
粤公网安备 44010502001741号
