深水网箱作为一种现代新型海洋设施养殖装备，具有养殖容量大、养殖效益高的优势。发展深水网箱养殖已成为中国沿海省份转变海水养殖方式、拓展海水养殖空间、缓解近海养殖压力的重要举措和有效途径^[1]。经过十余年的快速发展，截止2012年底，中国深水网箱总数量已超过8 000个，其中以HDPE(高密度聚乙烯)圆形重力式网箱占大多数，约为6 000个。网箱周长为40~80 m，深水网箱正朝着大型化方向发展。但国内深水网箱工程技术研究尚未跟上产业发展步伐，不同规格网箱尤其是大规格网箱基础理论的不足和技术参数的缺失使得网箱系统的设计、布局和安装盲目性很大，具有一定的安全风险。如2011年9月29日超强台风“纳沙”正面袭击中国海南临高深水网箱养殖基地，造成多数大规格网箱损坏，损失达数亿元。因此，针对中国常用的40~80 m周长的HDPE圆形重力式深水网箱，研究网箱在不同条件下的受力变形特性，获取高海况网箱关键力学技术参数，对于网箱的安全设计、安装具有重要指导意义。

在此之前的研究中，以40 m周长的HDPE圆形网箱为研究对象，通过数值模拟方法探讨了波浪流对深水网箱受力变形的影响，并对网箱计算模型的正确性及有效性进行了验证^[2-6]。该研究是在上述研究成果的基础上，基于建立的网箱计算模型，对几种主要规格网箱的锚绳力、波流力及容积损失率进行了数值计算，系统分析了不同网箱周长、浮管管径、网衣高度及网目大小对整体网箱受力变形的影响，旨在为网箱养殖业者进行科学合理的网箱选型提供一定的数据参考。

1.   网箱计算模型

深水网箱系统主要由浮架系统、网衣系统和锚泊系统组成，为较全面反映网箱养殖系统的受力变形情况，需要针对网箱各组成部件建立相应的计算模型，并对网箱整体进行模拟。

1.1   浮架系统

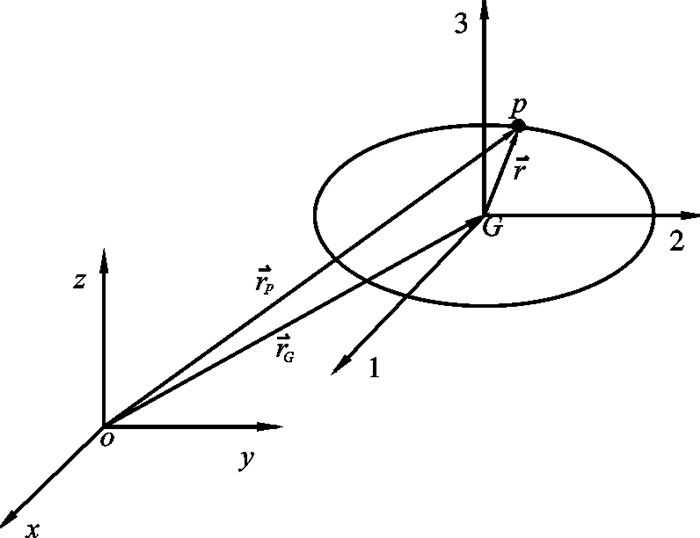
采用集中质量法将浮架离散为多个微元段进行受力分析，并将浮架各微元构件所受到的外力合力集中到浮架质心处，可建立整体坐标系下浮架的三维平动运动方程^[2]：

式中M_G为浮架总质量，N为浮架微元数，$ \ddot{X}_G$、$\ddot{X}_G $、$ \ddot{Z}_G$为浮架质心加速度，F_xi、F_yi、F_zi分别为第i个浮架微元所受外力在x、y和z方向的分力，可根据浮架微元所受到的重力、浮力、波流力以及与锚绳相连所受的锚绳张力进行矢量求和得到，其计算过程可参考文献[2]。

应用刚体运动学原理建立局部坐标系下浮架的转动运动方程为：

式中下标(1, 2, 3)代表局部坐标系统；ω₁、ω₂、ω₃为局部坐标系的角速度，I₁、I₂、I₃为浮架对1-2-3主轴的惯性矩，M_1i、M_2i、M_3i(i=1，N)分别为对1-2-3主轴的外力矩，可根据整体坐标系下求得的外力矩进行坐标变换获得^[2]。

1.2   网衣系统

采用集中质量法将网衣各网目离散成众多质点和构件，通过计算不同时刻各集中质量点的位移可得到网衣变形后的形状。网衣构件在波流作用下的受力包括重力、浮力、网线张力和波流力，利用牛顿第二定律建立网衣各质点的运动方程为^[3-4]：

式中N为质点相关构件的数量，$ \ddot{X}_i 、\ddot{Y}_i、\ddot{Z}_i$为质点加速度，P_j为重力与浮力的合力，T_j为网线张力，F_D和F_I为网衣构件上的速度力和惯性力，其计算表达式为：

式中 U_S 为构件自身速度，C_D、C_M、k_m分别为速度力系数、惯性力系数和附加质量系数，P为构件体积，e为构件单位向量。

分析网箱变形时可以采用切割法来计算网衣变形后的容积^[7]。可将圆柱体的高M等分，底面以切蛋糕的方式由圆心分割成N等分，弧线部分以直线来逼近，如此可将圆柱体切割成为M×N个三棱台，再将每个三棱台切分成3个四面体，因此可以得到3×M×N个四面体(图 1)。取四面体任意4个坐标点可以得到 A，B和C 3个向量，利用如下的向量三重积公式可以计算出每个四面体的体积，通过累加每个四面体的体积便可得到近似的网筒容积。可以推断此方法将网圆柱切割越细，计算结果就会越精确。笔者研究中M取值为网目群化后的网衣横向网目数，N取值为网衣纵向网目数的2倍。

图  1  切割法示意图

Figure  1.  Schematic diagram of division method

下载: 全尺寸图片 幻灯片

1.3   锚泊系统

网箱的锚泊系统与浮架相连将网箱限制在一定范围内运动。在波浪流冲击下网箱锚绳的受力可以间接反映网箱整体的力学特性。模拟锚绳时采用集中质量法将锚绳离散为构件与集中质量点进行分析，集中质量点位于构件的两端(图 2)。锚绳运动方程的建立与网衣相似，这里就不予重述。图 2中B_j为浮力、W_j为重力，T_j为锚绳张力，F_D、F_I分别为波流力中的速度力和惯性力。

图  2  锚绳质点与构件计算示意图

Figure  2.  Schematic diagram of the lumped mass point and the mooring line element for numerical calculations

下载: 全尺寸图片 幻灯片

2.   计算参数

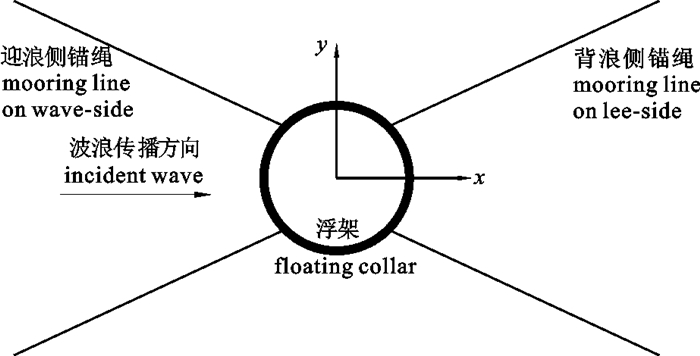
南海区常用的HDPE圆形重力式深水网箱周长为40~80 m。为叙述方便起见，在下文中均采用C40、C50、C60和C80分别表示40 m、50 m、60 m和80 m周长的网箱。网箱浮管管径为250~630 mm，网衣形状为圆柱形，网衣高度6~20 m，网目大小45 mm、75 mm和115 mm，网线直径3 mm，网衣缩结系数0.707。网衣配重大小对应4种规格C40~80网箱分别为400 kg、500 kg、600 kg和800 kg，以满足不同规格网箱沿圆周方向单位长度下网衣配重大小相同的条件，方便比较不同规格网箱的变形特性。网箱设置水深30 m，不同规格的网箱锚泊形式见图 3，C40和C50网箱设有4根锚绳，C60和C80网箱设有8根锚绳，且各种规格网箱的PE锚绳长度均为90 m，锚绳直径40 mm。

图  3  4种规格网箱布置示意图

Figure  3.  Schematic diagram of the four kinds of HDPE net-cages

下载: 全尺寸图片 幻灯片

由于国内外已有众多学者通过小比例尺模型试验^[8-14]、计算机数值模拟^[13-19]和海上实测^{[6, 20]}等手段围绕波浪流对网箱受力变形特性的影响开展了大量研究，为了避免重复研究，此研究只设定一种恶劣海洋工况条件(波高H=5 m，周期T=8 s，流速U=0.75 m · s^-1), 重点分析由于网箱规格不同对网箱受力变形的影响。在网箱数值计算过程中，设定初始时刻网箱锚绳受力、波流力、容积损失率均为0，波浪与水流的入射方向相同，均沿x轴正向入射。针对网衣的模拟采用网目群化方法以减少计算时间提高计算效率^[21-22]。

3.   计算结果及分析

3.1   网箱力学特性

表 1给出了4种不同规格网箱在波高H=5 m、周期T=8 s、流速U=0.75 m · s^-1条件下锚绳力和波流力的计算结果，表中列出的关于网箱浮管管径、网衣高度、网目尺寸参数为南海区应用的不同规格网箱的实际参数。表中的锚绳力是以各种规格网箱所有锚绳中受力最大的锚绳为选择依据的，即指波浪周期内网箱所受的锚绳力峰值。从表中数据可以得出，网箱所受的锚绳力、波流力均随着浮管管径和网衣高度的增加而增大，随网目的增大而减小，但相比浮管管径，网衣高度和网目大小对网箱锚绳受力的影响更明显。虽然浮管管径的变化对网箱整体受力影响不大，但在提供网箱浮力和抵抗网箱浮架变形方面，采用管径越大的浮管，网箱的安全系数越高，这也是C80网箱要配备大规格浮管的原因。

表  1  不同规格网箱锚绳力和波流力计算结果(H=5 m，T=8 s，U=0.75 m · s^-1)

Table  1.  Calculated results of the mooring line forces and wave-current forces of the net-cages

网箱周长/m perimeter of net-cage	浮管管径/mm pipe diameter	网衣高度/m net height	网目大小/mm net mesh size	锚绳力/kN mooring line force	波流力/kN wave-current force
40	250	6	45	17.4	33.5
			75	15.6	28.3
	280	6	45	18.5	34.5
			75	16.9	30.1
50	250	6	45	19.9	38.0
			75	17.4	31.6
	280	6	45	21.3	39.7
			75	18.5	32.8
	315	8	45	24.0	45.3
			75	20.9	37.3
60	280	8	45	23.5	52.7
			75	20.6	44.2
	315	8	45	25.5	56.8
			75	22.1	46.9
	420	10	45	29.2	66.2
			75	24.4	51.8
80	315	10	75	27.0	58.0
	420	12	75	29.3	61.6
			115	25.9	51.9
	630	20	75	39.3	85.0
			115	33.7	70.7

下载: 导出CSV 

| 显示表格

在相同条件下，当网箱规格增大时网箱受力增大。以C40和C50网箱为例，在浮管管径280 mm、网高6 m、网目45 mm条件下网箱锚绳力、波流力的增加幅度分别为2.8 kN、5.2 kN。比较C50和C60网箱，发现在浮管管径315 mm、网高8 m、网目75 mm条件下网箱锚绳力、波流力的增加幅度分别为1.2 kN、9.6 kN，网箱锚绳力增加幅度小的原因主要是因为C60网箱设置的锚绳数量是C50网箱的2倍，锚绳数量的增加导致锚绳受力的减小，这说明规格越大的网箱可以通过增加锚绳数量的简单方法来提高网箱锚泊系统的安全性。

对比网箱锚绳力和波流力的计算结果可以发现，由于不同网箱锚绳数量的差异，对于C40和C50网箱，网箱所受的最大锚绳力略大于网箱所受波流力的50%；对于C60和C80网箱，网箱所受的最大锚绳力略小于其波流力的50%。

3.2   网箱变形特性

4种不同规格网箱在波高H=5 m、周期T=8 s、流速U=0.75 m · s^-1条件下网箱变形的计算结果见表 2，表中的容积损失率定义为1-V_p/V_p0，其中V_p为网箱变形后的容积，表中列出的网箱容积即为网箱变形后的容积，V_p0为无波流作用时的网箱初始容积。可以看出，不同规格网箱的最大容积损失率变化范围为44.7%~60.2%，平均值为52.5%，网箱变形比较大。结合此前研究结果^[4]，建议网箱养殖区域应选择流速小于0.75 m · s^-1的海区较为适宜，以减少网箱容积损失率，增大养殖鱼类活动空间。

表  2  不同规格网箱变形计算结果(H=5 m，T=8 s，U=0.75 m · s^-1)

Table  2.  Calculated results of the net deformation of the net-cages

网箱周长/m perimeter of net-cage	浮管管径/mm pipe diameter	网衣高度/m net height	网目大小/mm net mesh size	网箱容积/m3 net-cage volume	容积损失率/% volume reduction rate
40	250	6	45	331.6	56.6
			75	378.2	50.5
	280	6	45	315.5	58.7
			75	364.4	52.3
50	250	6	45	539.7	54.8
			75	600.6	49.7
	280	6	45	526.6	55.9
			75	591.0	50.5
	315	8	45	636.8	60.0
			75	708.4	55.5
60	280	8	45	1 070.4	53.3
			75	1 196.4	47.8
	315	8	45	1 015.4	55.7
			75	1 159.8	49.4
	420	10	45	1 140.3	60.2
			75	1 286.4	55.1
80	315	10	75	2 597.4	49.0
	420	12	75	2 994.9	51.0
			115	3 379.9	44.7
	630	20	75	4 196.6	58.8
			115	4 481.8	56.0

下载: 导出CSV 

| 显示表格

从表 2可以得出，相同条件下大规格网箱的容积损失率更小。以C50和C60网箱为例，在浮管管径315 mm、网目75 mm条件下，2种网箱的容积损失率分别为55.5%和49.4%，后者小于前者6.1%，C60网箱变形后的容积为1 159.8 m³，约为C50网箱的1.64倍。因此，仅从网箱变形方面考虑，大规格网箱因具有更大的鱼类养殖空间，其养殖效果会更好。

对于各种不同规格的网箱，浮管管径对网箱容积损失率的影响较小，但网衣高度和网目大小对网箱变形具有显著影响。以C80网箱为例，网目75 mm条件下网箱容积损失率从网高10 m时的49%增大到网高20 m时的58.8%，增加幅度为9.8%；网高12 m时网箱容积损失率从网目75 mm时的51%减小为网目115 mm时的44.7%，减小幅度为6.3%。但当网衣高度为20 m时该2种网目大小条件下的容积损失率差值仅为2.8%，说明随着网衣高度的增加，网目大小的变化对网箱变形的影响减小。

4.   结语

通过对40~80 m周长HDPE深水网箱分别在不同浮管管径、网衣高度和网目大小组合条件下网箱受力变形计算结果的比较和分析，发现网箱锚绳受力、波流力和容积损失率均随着网衣高度的增加而增大，随网目的增大而减小，浮管管径的增大对网箱整体受力变形的影响较小。当网箱规格增大时，网箱锚绳受力、波流力增大，容积损失率减小，网目大小对网箱变形的影响随着网衣高度的增加而有所减小，锚绳数量的增加可以大大降低锚绳受力，为深水网箱大型化发展提供了一定的理论参考依据。