Design and making of truncated cone cod-end of deep-water net cage
-
摘要:
深水网箱囊网受水流推动,形状随水阻力大小而变化。囊网形状的变化与养殖容积有关,并直接影响了网箱养殖效果。通过分析认为,圆台形重力式柔性囊网有较好的抗流效果,更适合于深水网箱养殖作业。通过实物试验,报道了圆台形囊网在流速0.45~0.75 m · s-1时的外形设计、配重及制作方法,为强流下的深水网箱囊网制作提供参考。
Abstract:The cod-end of deep-water net cage is driven by the current. Its form changes with the size of water resistance. The change of cod-end form is related to the carring capacity of net cage and influences the cultural effect directly. The anti-current effect of truncated cone cod-end is better than that of circular and column cod-ends by analysis, and is more suitable for the operations of deep-water net cage culture than circular and column cod-ends. By practical tests, this paper reported the form design, sinker weight and making method of the truncated cone cod-end under current velocity of 0.45~0.75 m · s-1, and provided reference for cod-end making of deep-water net cage at strong current.
-
网衣系统是深水网箱的主要组成部分,在维持鱼类生长空间、防止鱼类逃逸和敌害侵袭、保持箱体内外水体交换畅通方面起着主导作用,高海况条件下网衣是否安全与可靠直接关系到养殖生产的经济效益和可持续发展。网衣也是网箱系统中受力最为复杂的部件之一,在水流作用下网衣所受到的外力中水流力与网衣的变形具有高度的相互依赖性,即网衣在水流作用下会发生运动变形,而当网衣形状发生变化后,作用在网衣上的水流力也将随之发生变化,这与工程上的一般刚性结构物有着很大的不同,网衣的这些特征正是数值计算时所需要解决的问题。近年来,国内外关于网衣水动力特性的研究已有不少,SUZUKI等[1]和TAKAGI等[2]采用质量弹簧单元的方法模拟了渔网的动力学性能。詹杰民等[3-4]、李玉成和桂福坤[5]、WAN等[6-7]对水流作用下平面网衣的受力进行了研究。LADER和ENERHAUG[8]、LADER和FREDHEIM[9]、HUANG等[10-11]、LI等[12]、ZHAO等[13]及LEE等[14]均采用集中质量法将网衣离散成众多质点进行模拟,结合物理模型试验研究了不同海况条件下圆形网箱的水动力特性。在上述所列文献中,无论是有关平面网衣还是圆形网衣的研究,其内容都是研究网衣达到稳定状态后的水动力特性情况,而对水流作用下网衣达到稳定状态前受力与变形的变化过程研究,目前国内还未见相关报道。
在此之前的研究已分别对平面网衣和圆形网衣的运动变形特性进行了数模研究[15-16],建立了网衣数学模型,并利用前人的试验结果对数学模型进行了验证,结果吻合较好。该研究是在上述研究成果的基础上,基于建立的网衣数学模型,分别对水流作用下网衣所受的水流力、网衣形状和网衣运动位移三者随时间的变化过程进行了数值模拟,旨在探讨和分析网衣在水流作用过程中的动态变化规律。
1. 网衣数学模型
利用集中质量法将柔软的网衣分解成众多质点和构件组成的离散模型,集中质量点设于每个网目目脚的两端(图 1)。在计算作用在目脚上的外力时,可以将单个目脚看作为一个构件,其在水流作用下的受力由重力、浮力、网线张力和水流力组成,具体数学表达式在文献[16]已作详细介绍。
整体坐标系下单个质点的受力情况见图 2,利用牛顿第二定律建立如下的网衣各集中质量点的运动方程。图 2中的T1、T2、T3和T4为网线张力,FD和FI为水流力中的速度力和惯性力。
$$ m_i X_i=\sum\limits_{j=1}^N F_{D X j}+F_{I X j}+T_{x j} $$ (1a) $$ m_i Y_i=\sum\limits_{j=1}^N F_{D Yj}+F_{I Y j}+T_{Y j} $$ (1b) $$ m_i Z_i=\sum\limits_{j=1}^N F_{D Z j}+F_{I Z j}+P_j+T_{Z j} $$ (1c) 式中N为质点相关构件的数量,X、Y和Z为质点的加速度,Pj为重力与浮力的合力。
根据Morison方程,网衣构件上的水流力计算表达式可表示为如下形式,其中等式右边第一项表示网衣构件的速度力,第二项表示水体的附加质量力,第三项表示网衣构件排开水体的惯性力。
$$ \begin{aligned} & F_c=F_D+F_I=\frac{1}{2} \rho_w C_D S\left|\boldsymbol{U}-\boldsymbol{U}_{\mathrm{S}} \cdot \mathbf{e}\right|^2 \mathbf{e}+ \\ & \rho_w V_0 C_M \frac{5 \boldsymbol{U}}{5 t}-\rho_w V_0 k_m \frac{5 \boldsymbol{U}_S}{5 t} \end{aligned} $$ (2) 式中US为构件自身速度,CD为速度力系数,CM=1+km为惯性力系数,km为附加质量系数,V0为构件体积,e为构件单位向量。
由于网衣运动方程(1)属于下述形式的二阶微分方程,可以利用四阶Runge-Kutta方法进行数值求解[17],相关数学表达式为:
$$ \xi=F t, \xi \xi $$ (3) 质点的位移ξ和速度ξ可以表达为:
$$ \begin{aligned} & \xi t+\Delta t=\xi t+\Delta t \cdot \xi(t)+\Delta t^2 \cdot\left(k_1+k_2+\right. \\ & \left.k_3\right) /6 \end{aligned} $$ (4a) $$ \xi t+\Delta t=\xi^{\prime} t+\Delta t \cdot \quad k_1+2 k_2+2 k_3+k_4 \\ /6 $$ (4b) 式中k1、k2、k3和k4分别为:
$$ k_1=F t, \xi t, \xi t $$ $$ k_2=F t+\frac{\Delta t}{2}, \xi t+\frac{\Delta t}{2} \xi t, \xi t+\frac{\Delta t}{2} k_1 $$ $$ k_3=F t+\frac{\Delta t}{2}, \xi t+\frac{\Delta t}{2} \xi t+\frac{\Delta t^2}{4} k_1, \xi t+\frac{\Delta t}{2} k_2 $$ $$ k_1=F t+\Delta t, \xi t+\Delta t \xi_t+\frac{\Delta t^2}{2} k_2, \xi t+\Delta t k_3 $$ 网衣的配重采用底框设计,目的是减少网衣的变形。该文基于集中质量点法将底框离散成众多微元构件,并将底框视为刚体处理。在运动分析时将各个微元构件所受到的外力合力累加到底框的质心处,相当于只对一个质点建立6个自由度上的运动方程,从而简化了计算。有关底框具体的数学方程可参考文献[18],这里不作详细叙述。
2. 数学模型的验证
关于网衣数学模型的正确性和有效性的验证,黄小华等[16]已针对LADER和ENERHAUG[8]的网衣试验情况进行了数值模拟,给出了各种流速下网衣所受的水流力和网衣容积损失率的计算结果(表 1)。结果表明,在各种不同的流速条件下,网衣受力与变形的计算结果与试验结果十分接近,误差值基本上都在10%以内。
表 1 不同流速条件下的计算和试验结果比较Table 1. Comparison of calculated and experimental results under different current velocities流速/m·s-1
velocity容积损失率/% volume reduction rate 水流力/N drag force 试验值
experimental value计算值
calculated value绝对误差
absolute error试验值
experimental value计算值
calculated value相对误差/%
relative error0.13 1 1 0 12.02 12.14 1 0.21 5 4 1 21.97 23.97 9 0.26 11 8 3 34.96 35.37 1 0.33 24 19 5 49.79 44.39 11 0.52 36 34 2 88.01 82.03 7 3. 计算参数的选取
圆柱形网衣初始形状如图 3所示,网衣顶端固定,网衣底端处设有一根长为40 m的金属钢圈作为配重。网衣周长40 m,高度9.6 m,网目大小2a=75 mm,网线直径d=3 mm,网衣材质为PE(ρ=953kg · m-3),横向网目数为896目,缩结系数0.6;纵向网目数为160目,缩结系数0.8。在数值计算中,水流方向为x方向,海水的密度ρw=1 030 kg · m-3,重力加速度g=9.81m · s-2,附加质量系数km=1.0。配重大小为GW1=400 kg与GW2=800 kg 2种,水流速度取U=0.3 m · s-1、0.4 m · s-1、0.5 m · s-1和0.6 m · s-1。
由于计算中的网衣结点数太多(287 616个),笔者采用网目群化方法[19-20]将相邻16×16个网目合并为1个等效大网目(结点总数减少到1 176个),以减少计算时间提高计算效率。
4. 计算结果及分析
4.1 网衣变形
图 4给出了配重GW1、U=0.4 m · s-1时网衣稳定前不同时刻的动态变形情况。可以很明显地看出网衣在运动开始阶段(t<5 s)变形很快,随着水流作用时间的延长,底框倾角从水平开始逐渐增加,网衣在底框以及网线张力的作用下变形幅度逐渐减慢,网衣各结点运动速度减小,并最终在t=50 s时因受力平衡达到稳定状态后而停止运动。
图 5和表 2为不同配重和流速条件下网衣达到稳定状态后的变形模拟结果。可以直观地看出流速增加会加剧网衣的变形。以配重GW1为例,当流速U=0.3 m · s-1时网衣容积损失率较小(14%),流速U=0.6 m · s-1时网箱容积损失率高达41%,后者约为前者的3倍。当网衣底端配重增加到800 kg时网衣容积损失率减小,变形改善明显。在流速U=0.6 m · s-1时和增加配重后,容积损失率减少了16%,表明了配重及流速大小对网衣变形具有显著影响。
4.2 水流力
图 6为水流作用下网衣所受水流力的变化历时曲线,实线代表配重GW1下的计算值,虚线代表配重GW2下的计算值。从图 6可以看出,在水流作用网衣的初始阶段,水流力呈现先减小后增加的变化趋势,随着水流作用时间的延长,水流力的震荡幅度越来越小,水流力的历时曲线近乎一条平行于横坐标轴的直线。其原因主要是因为水流力的大小与网衣构件速度密切相关,并和它具有一定的反比关系,当网衣离开t=0 s时刻的初始位置而发生运动时,水流的冲击作用能使网衣的运动速度在短时间内迅速达到最大,这时网衣所受水流力最小,随后在配重系统的影响和网线张力逐渐增加的情况下,网衣的运动速度会逐渐减小直至网衣达到一个相对稳定的状态。
比较不同配重和流速条件下水流力的计算结果(表 2)可以发现,配重或流速的增加都会使得网衣所受水流力作用加大,表明了配重及流速大小对网衣受力同样具有显著影响。
表 2 网衣稳定后的水流力和容积损失率计算值Table 2. Calculated results of drag force and volume reduction rate流速/m·s-1
velocity水流力/kN drag force 容积损失率volume reduction rate GW1 GW2 GW1 GW2 0.3 4.04 5.64 14% 8% 0.4 5.72 7.98 23% 13% 0.5 7.49 10.01 32% 19% 0.6 8.87 12.54 41% 25% 4.3 网衣底端位移
图 7为网衣底端中心点坐标的历时曲线。可以看出,在水流作用网衣过程中网衣底端中心点的水平和垂向坐标值都随着时间的递增而缓慢增加,直至网衣稳定时达到最大。当增加流速时网衣底端的水平和垂向坐标值都增加。配重GW1条件下,流速U=0.3 m · s-1时水平坐标最大值为2.04 m,垂向坐标最大值为-8.42 m;流速U=0.6 m · s-1时水平坐标最大值为4.2 m,垂向坐标最大值为-5.72 m,后者分别增加2.16 m和2.7 m。对于不同流速,当配重增加时网衣底端的水平和垂向坐标值都显著减小。
5. 结语
该文基于建立的网衣数学模型对圆型网衣的动态变化过程进行了数模研究,给出了不同条件下网衣所受的水流力、网衣动态变形以及网衣底端特定点位移的计算结果。可以发现,在水流作用网衣的初始阶段,网衣变形较快,所受的水流力呈现出先减小后增加的变化趋势,随着水流作用时间的延长,网衣的受力、变形和运动都能达到一个稳定的状态。水流速度增加会加剧网衣的运动变形,且使网衣所受的水流力增加;当网衣底端配重增加时,网衣的运动变形会显著减小,但网衣所受的水流力将明显增加。
-
表 1 网衣在冲角90°时阻力的估算
Table 1 Resistance of webbing at attack angle of 90°
流速(m·s-1)
velocity of flow0.45 0.55 0.65 0.75 计算公式
calculation equation阻力(N)
resistance31 933.44 47 703.04 66 626.56 88 704.00 日本田内
$ R_{90}=1760 \frac{d}{a} S \cdot V^2$24 502.91 35 811.94 49 116.69 64 306.28 A.C.列维恩
$ R_{90}=1860 \frac{d}{a} X \cdot H \cdot S \cdot V^{1.89}$31 479.84 47 025.44 65 680.16 87 444.00 湛江水产学院等
$R_{90}=\left(880 \frac{d}{a}-10\right) S \cdot V^2 $表 2 网衣在4种流速下的平均阻力
Table 2 Mean resistance of webbing at 4 different velocity of flow
流速(m·s-1) velocity of flow 0.45 0.55 0.65 0.75 阻力(N) resistance 26 112 38 743 53 812 71 281 表 3 修正后网衣在4种流速下的平均阻力
Table 3 Revised mean resistance of webbing at 4 different velocity of flow
流速(m·s-1) velocity of flow 0.45 0.55 0.65 0.75 阻力(N) resistance 18 592 27 585 38 314 50 752 表 4 4种流速下的配重
Table 4 Sinker weight at 4 different velocity of flow
流速(m·s-1) velocity of flow 0.45 0.55 0.65 0.75 配重(t) sinker weight 1.9 2.9 4.0 5.4 表 5 纲索用量
Table 5 Use level of cable
缘纲(m,ф6mm)
bolchline横力纲(m,ф12mm)
cross cable竖力纲(m,ф6mm)
vertical cable网线(m,ф2mm)
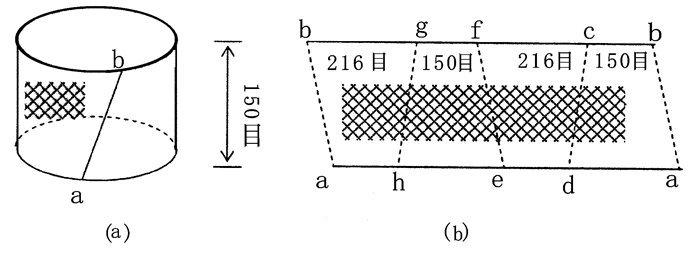
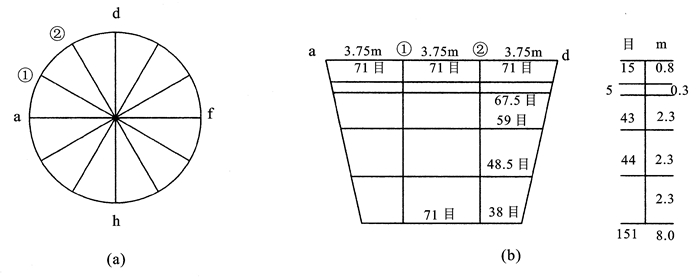
netting twine网盖 cover of net 50 50;16×2 若干 网身 net body 50;49;48;44;38 10 m×12~16 若干 网底 bottom of net 35 35;14×4 若干 -
[1] Fredriksson D W, Swift M R, Irish J D, et al. Fish cage and mooring system dynamics using physical and numerical models with measurements[J]. Aquacultural Engin, 2003, 27(2): 117-146.
[2] 黄锡昌. 捕捞学[M]. 重庆: 重庆出版社, 2001.69-77. https://xueshu.baidu.com/usercenter/paper/show?paperid=c43e118ff5d0ecc751d1d09ce567f712&site=xueshu_se [3] 詹杰民, 胡由展, 赵陶, 等. 渔网水动力试验及分析[J]. 海洋工程, 2002, 20(2): 49-53. doi: 10.3969/j.issn.1005-9865.2002.02.009 -
期刊类型引用(8)
1. 唐元龙,谢迎春,袁昊训,李相坤. 聚乙烯网衣破损因素下的水动力特性与流场模拟. 渔业现代化. 2024(06): 20-30 .  百度学术
百度学术
2. 黄小华,刘海阳,胡昱,陶启友,王绍敏,袁太平. 深水养殖网箱浮架变形模拟及结构改进设计. 农业工程学报. 2018(15): 44-49 .  百度学术
百度学术
3. 黄小华,刘海阳,胡昱,陶启友,王绍敏,袁太平. HDPE圆形网箱单点系泊与多点系泊受力特性模拟分析比较. 浙江海洋大学学报(自然科学版). 2018(02): 140-146 .  百度学术
百度学术
4. 陈天华,潘昀,冯德军,孟昂,桂福坤. 固定方式对水流作用下桩柱式围网网片力学特性的影响. 水产学报. 2018(03): 452-460 .  百度学术
百度学术
5. 桂福坤,陈天华,赵云鹏,董国海. 固定方式对桩柱式围网网片波浪力学特性影响研究. 大连理工大学学报. 2017(03): 285-292 .  百度学术
百度学术
6. 李杰,晏磊,杨炳忠,张鹏. 罩网自由沉降过程的数值模拟研究. 南方水产科学. 2017(04): 105-114 .  本站查看
本站查看
7. 陈天华,孟昂,桂福坤. 波浪高度及方向对桩柱式围网养殖系统网片水力特性的影响. 农业工程学报. 2017(02): 245-251 .  百度学术
百度学术
8. 陈天华,潘昀,孟昂,桂福坤. 桩柱式围网单元网片在水流作用下的水动力特性研究. 水动力学研究与进展(A辑). 2017(04): 511-519 .  百度学术
百度学术
其他类型引用(6)




 下载:
下载:






 粤公网安备 44010502001741号
粤公网安备 44010502001741号
