Fish stock assessment based on abundance index and resilience: a case study of largehead hairtail in Sea of Japan and East China Sea
-
摘要: 为了解日本海和东海带鱼 (Trichiurus japonicus) 渔业资源状况，利用一种基于丰度指数的评估模型 (Abundance maximum sustainable yields, AMSY) 对2个海域的带鱼资源进行了评估。结果显示，2个海域的带鱼渔业在20世纪90年代至21世纪00年代的大部分时间里相对资源量水平 (B/BMSY) 低于1，而相对捕捞死亡水平 (F/FMSY) 高于1，处于过度捕捞状态。AMSY模型里相对最大可持续产量 (MSYq) 和MSY水平下的捕捞死亡系数 (FMSY) 等参数评估结果对不同内禀增长率 (r) 先验分布范围比较敏感，而B/BMSY和F/FMSY等生物学参考点评估结果对特定年份的相对资源量水平 (Bt/k) 先验分布范围的下限设置比较敏感。AMSY模型仅需要单位捕捞努力量渔获量 (Catch per unit effort, CPUE) 数据、评估对象的r和特定年份的Bt/k水平先验信息，可以评估基于MSY的生物学参考点 (B/BMSY和F/FMSY)，适合无统计产量数据的海域内渔业资源评估。
-
关键词:
- 带鱼 /
- 单位捕捞努力量渔获量 /
- 剩余产量模型 /
- 数据缺乏 /
- 资源评估
Abstract: In order to understand the exploitation status of largehead hairtail (Trichiurus japonicus) fisheries in the Sea of Japan and the East China Sea, we used a fishery assessment model based on abundance index (Abundance maximum sustainable yields, AMSY) to assess the two fisheries. The results show that during most of the 1990s and 2000s, the relative biomass levels (B/BMSY) of the largehead hairtail fisheries in the two seas were lower than 1, but the relative fishing mortality levels (F/FMSY) were higher than 1, which indicates an overfished state. The estimated parameters such as relative maximum sustainable yield (MSYq) and relative fishing mortality at MSY level (FMSY) of the AMSY model were more sensitive to different prior distribution ranges of intrinsic rate of increase (r), while the estimated biological reference points (BRPs), i.e., F/FMSY and B/BMSY were more sensitive to the lower limit of different prior distribution ranges of relative biomass level (Bt/k). AMSY can estimate the BRPs of the target fisheries under MSY framework using only catch per unit effort (CPUE) data, prior information of r and relative biomass level for a specific year. AMSY is appropriate for fishery stock assessment in the sea areas where lack statistical data of catches. -
海洋渔业资源是重要的动物蛋白和微量营养物质来源，并为沿海地区的人们提供就业机会和收入[1]。近几十年来，过度捕捞导致已开发种群持续枯竭，全球海洋渔业捕捞产量一直停滞不前[2]。资源评估是实施渔业科学管理和维系可持续发展的一项基础工作。随着计算机运算能力的提高和多学科协作，渔业资源评估方法得到迅速发展，评估模型的类型趋于多样化，结构变得更加复杂[3]。传统的评估模型往往需要较完善的统计和调查数据，包括产量、丰度指数甚至年龄或体长结构等。然而，大多数的已开发渔业种群，特别是发展中国家的，缺乏开展资源评估所需的数据。因此，全球只有20%的渔获量来评估种类，且这些种类仅占所有种类数量不足1%[4]。近年来，渔业学者已逐渐意识到以上问题的严重性，一些数据有限条件下资源评估的替代方法正在逐步建立起来[5-7]。
当前，基于产量数据和基于体长数据两类数据有限条件下的评估方法已在我国开展应用。基于产量的评估方法可以利用统计产量数据和辅助信息 [比如内禀增长率 (r) 和自然死亡系数等] 评估目标种群的最大可持续产量 (Maximum sustainable yield, MSY) 及相关生物学参考点 [如相对资源量水平 (B/BMSY) 和相对捕捞死亡水平 (F/FMSY)] [5]，此类方法已在我国四大海区的主要经济种类中得到应用[8-10]；基于体长的评估方法可以利用体长频率分布数据评估鱼类种群的生长、死亡参数和开发状态等。其中，电子体长频率分析法 (Electronic length frequency analysis, ELEFAN) 是过去很长一段时间内我国渔业资源的主要评估手段，但其评估的开发率并不能很好地判断渔业开发状态，尤其是热带、亚热带海域的鱼类往往能承受较高的开发率[11]；基于体长的贝叶斯生物量评估方法 (Length-based Bayesian biomass estimation, LBB)[6]是一种用于估算B/BMSY和Lc/Lc_opt (首次捕捞长度与最佳开捕长度的比值) 等参考点的新方法，已在我国北部湾、闽江河口和南沙岛礁等重点海域的鱼类种群中得到应用[12-14]。
我国的渔业产量统计数据多以行政区域进行统计，当前基于产量数据的渔业资源评估主要应用于四大海区的主要经济鱼种[8-10]。由于缺乏统计产量数据，诸如北部湾等重点海域，难以采用此类模型开展渔业资源评估工作。另外，基于体长的方法[8,14]评估的准确性高度依赖体长频率分布数据，使用选择性较强的网具往往容易造成堆积效应 (Pile-up effect)，使得参数评估出现偏差，而在实际科研调查取样中往往使用单种网具采样，所采集的体长频率分布数据不能很好地反映鱼类种群的真实情况。当前，我国的渔业科研单位在近海重点海湾和河口积累了较长时间序列的调查数据，在无统计产量数据的情况下，如何开展重点海域关键渔业种群资源评估已成为亟需开展的工作。本研究利用一种基于丰度指数和恢复力的渔业资源评估方法 (Abundance maximum sustainable yields, AMSY)[7]，对日本海和东海带鱼 (Trichiurus japonicus) 渔业的B/BMSY和F/FMSY等进行评估，旨在为该方法在我国近海重点海域的应用提供依据和参考。
1. 材料与方法
1.1 数据来源
带鱼是西北太平洋海域重要的经济鱼种，以往研究中，黄渤海和东海带鱼被认为是2个独立的种群。在黄渤海沿岸产卵，冬季于济州岛西部越冬的为黄渤海种群；在温州湾沿岸产卵，于东海中南部越冬的为东海种群[15]。也有研究认为东海、黄渤海一直到对马暖流海域的带鱼个体群可看作一个种群，即日本海-东海带鱼种群，资源主要由中韩日三国共同开发[16]。本研究分别采用日本海和东海带鱼渔业的单位捕捞努力量渔获量 (Catch per unit effort, CPUE)数据进行分析，利用AMSY模型对其生物学参考点进行评估。
日本海带鱼在2000年以前主要由大型底拖网和近岸底拖网捕获，2种作业方式占整个资源渔获量的70%~80%，近年来带鱼资源的衰退使得其产量不断下降[16]。因此，本研究采用日本海大型底拖网和近岸小型底拖网的带鱼CPUE (kg·网−1) 作为该渔业的丰度指数，研究数据来自日本水产厅 (https://www.jfa.maff.go.jp/)，时间跨度为1981—2009年[16]。其中，大型底拖网带鱼渔业CPUE呈明显的下降趋势，2000年后的CPUE (约3 kg·网−1) 仅为20世纪80年代 (约30 kg·网−1) 的1/10；近岸小型底拖网带鱼渔业CPUE处于波动状态，2000年后的年均CPUE (3.4 kg·网−1) 比2000年前的(4.3 kg·网−1) 有明显下降 (图1)。
![]()
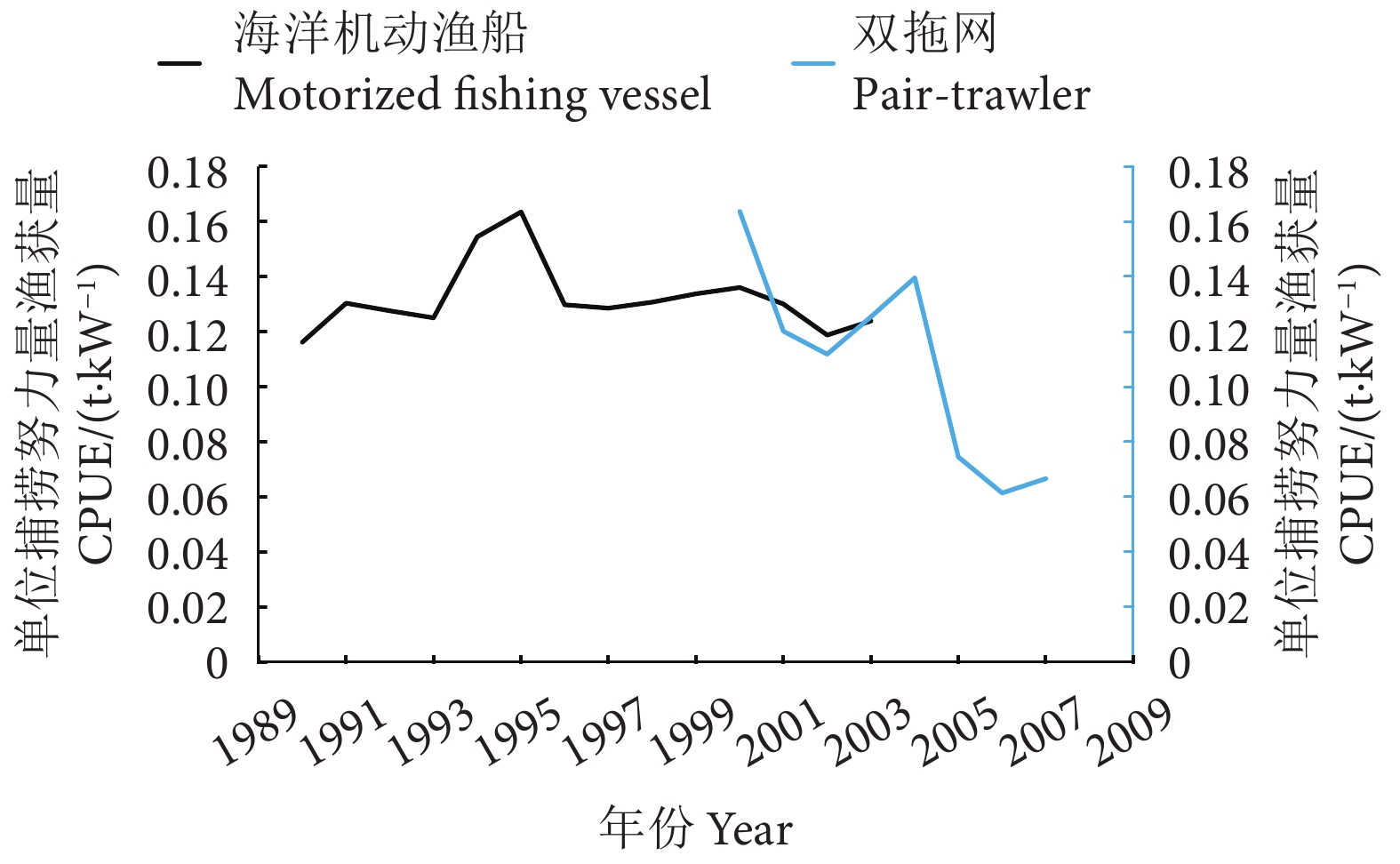
图 1 1981—2009 年日本海带鱼大型底拖网和近岸底拖网渔业单位捕捞努力量渔获量Figure 1. CPUE of largehead hairtail fisheries by large bottom trawl and offshore bottom trawl in Sea of Japan from 1981 to 2009东海带鱼是我国最具价值的捕捞对象之一，主要作业方式为底拖网 (包括单拖和双拖)和帆张网，其产量多年来居各经济鱼类之首，在我国海洋渔业中占据重要地位[17-19]。本研究采用的东海带鱼CPUE数据来自东海带鱼资源动态监测系统 (由浙江省海洋水产研究所实施)，其中，1990—2003年CPUE 数据为东海区海洋机动渔船 (包含拖网、帆张网等作业方式) 的带鱼CPUE (t·kW−1)，2000—2007年CPUE 数据为双拖生产监测的带鱼CPUE (kg·h−1)[20]。东海与日本海带鱼渔业的CPUE数据类似，在2000年以后也出现了下降 (图2)。
![]()
图 2 东海带鱼渔业单位捕捞努力量渔获量Figure 2. CPUE of largehead hairtail by marine motorized fishing vessels and pair-trawler in East China Sea1.2 AMSY模型
根据剩余产量模型的基本假设，某个种群t+1年的生物量 (Bt+1) 可以表示为t年的生物量 (Bt) 加上t年的剩余产量 (Yt) 再减去t年的渔获量 (Ct)，即[7]：
Bt+1=Bt+Yt−Ct=Bt+Btr(1−Btk)−Ct (1) 式中：r为种群内禀增长率；k为环境容量。
在渔业资源评估中，CPUE (A)通常被作为资源丰度的指标，并通过可捕系数q与生物量直接相关[7]：
At=Btq (2) 通过组合公式 (1) 和 (2)，可以得到[7]：
At+1=At+Atr(1−Atkq)−Ctq (3) 在无统计产量数据的情况下，为了评估鱼类种群的相对开发状态，可以不需要获得Ct、Bt、k和q的绝对值，用相对产量Cqt替换Ctq，相对环境容量kq替换kq，然后由公式 (3) 变换得到[7]：
Cqt=At+Atr(1−Atkq)−At+1 (4) 在Schaefer剩余产量模型中[21]，FMSY=r/2，BMSY=k/2，MSY可以通过rk/4得到，因此，根据公式 (4) 变换后的MSYq可以用rkq/4表示[10]。MSYq为相对产量Cq对应的MSY，因此，CqMSYq的值与相对产量 (C/MSY) 的值相等。同样地，At/kq的值与Bt/k的值相等，捕捞死亡系数(F) 的计算公式Ct/Bt可以用Cqt/At的值计算[7]。生物学参考点F/FMSY可以用以下公式计算[7]：
FFMSY=CqtAtr/2=2CqtrAt (5) 模型中参数kq的先验可以通过At/(Bt/k)得到，而参数BMSY_q的值通过kq/2得到。通过方差与协方差矩阵 (VCM) 对参数组合r-kq进行多元对数正态随机取样[7]：
VCMlog(r),log(kq)={σ2log(r)covlog(r),log(kq)covlog(r),log(kq)σ2log(kq)} (6) 式中：cov为2个参数分布的协方差；σ2为方差。
基于马尔可夫链蒙特卡罗 (MCMC) 的过滤器[7]用来协助寻找与CPUE数据和先验信息相匹配的r-kq参数组合，所有的r-kq参数组合针对剩余产量和 CPUE 使用不同的随机误差设置进行了多次测试，多次测试均未通过MCMC过滤器时便会被排除在进一步处理之外。这个过程会导致模拟的CPUE时间序列与观察到的略有不同，因为模型会导致不切实际的捕获量或生产力曲线中的峰和谷被平滑[7]。模型运行在R语言 (版本4.0.3) 中完成，模型代码源自德国基尔亥姆霍兹海洋研究中心 (http://oceanrep.geomar.de/)。
1.3 先验信息设置与敏感性分析
AMSY模型需要时间序列的CPUE数据、r的先验分布范围以及特定年份的相对种群资源量水平 (Bt/k) 先验信息。AMSY模型推荐在无相关研究的情况下，种群参数r的先验分布范围设置参照Fishbase (www.fishbase.org) 的恢复力分级表[7]。本研究采用Zhang等[9]对东海带鱼种群的评估结果，r先验分布范围设置为均匀分布 (0.42, 0.72)，这一分布范围比Fishbase推荐的 (0.2, 0.8) 更为精确[9]。特定年份的Bt/k先验信息可以通过LBB模型等方法评估得到，本研究采用Zhang等[9]基于Catch-MSY模型以及张魁和陈作志[18]基于贝叶斯状态空间模型对东海带鱼的评估结果，特定年份选取为2000年，Bt/k的范围设置为(0.15, 0.4)。另外，为探讨模型对先验信息的敏感性，分析了不同r和Bt/k的先验分布对日本海大型底拖网带鱼渔业评估结果的影响。本研究采用的4组r先验分布范围分别为 (0.32, 0.72)、(0.42, 0.72)、(0.42, 0.82) 和 (0.32, 0.82)，4组Bt/k先验分布范围分别为 (0.05, 0.4)、(0.15, 0.4)、(0.15, 0.5) 和 (0.05, 0.5)。
2. 结果
2.1 日本海带鱼渔业
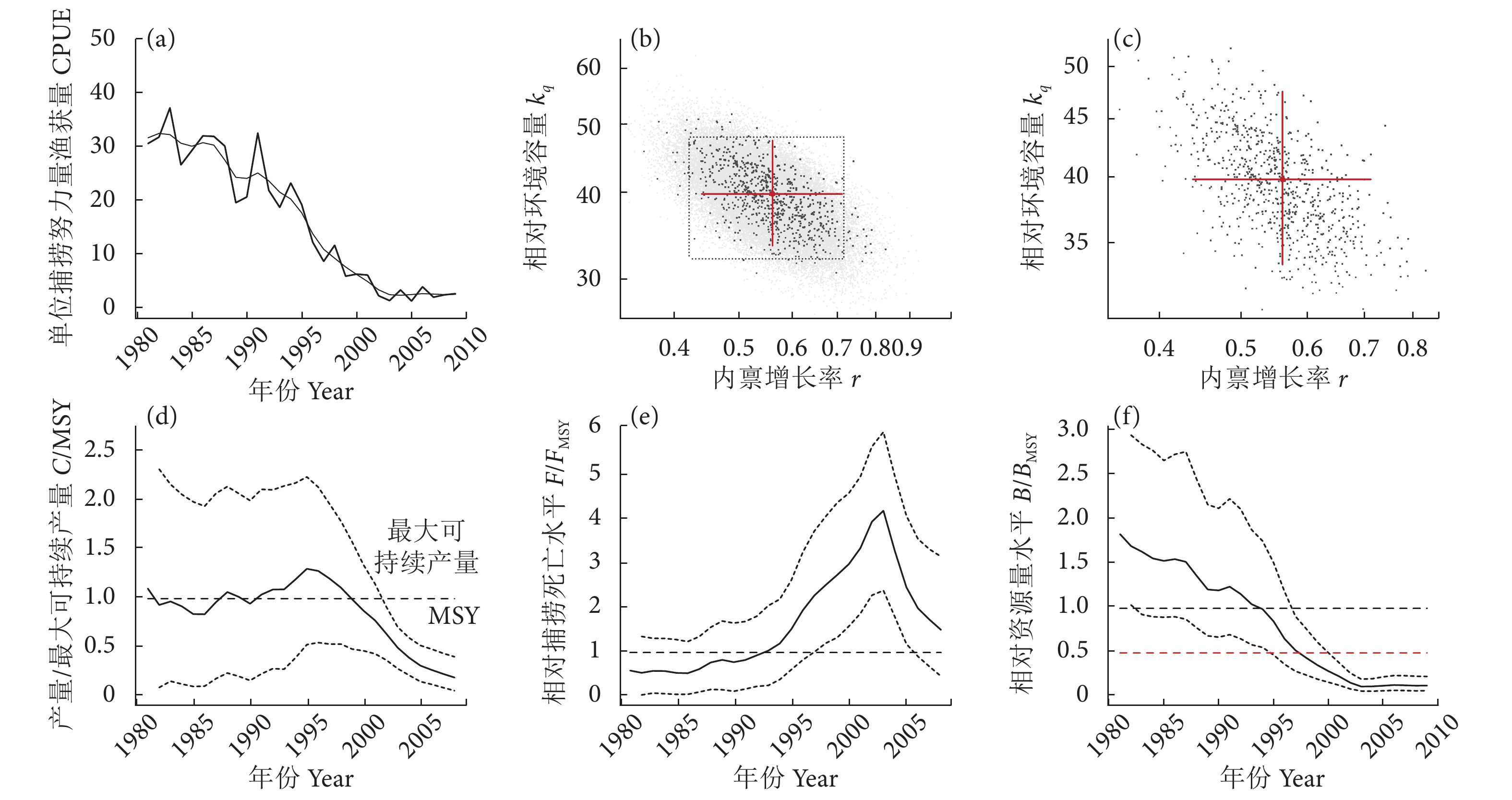
基于大型底拖网CPUE评估的日本海带鱼渔业结果 (图3) 显示，1981—2000年产量在MSY附近波动，之后便一直处于MSY之下 (图3-d)；F自1981年开始一直处于上升趋势，自1995年开始超过FMSY，F/FMSY在2003年达到最高值 (4.256) 后处于下降趋势，但是2009年的F/FMSY仍大于1 (图3-e)；B/BMSY自1981年起一直处于下降趋势，1995年开始低于1，1998年以后低于0.5 (图3-f)。评估的参数r为0.572，FMSY为0.286，2000年的C/MSY、F/FMSY和B/BMSY分别为0.99、2.68和0.37 (表1)。
![]()
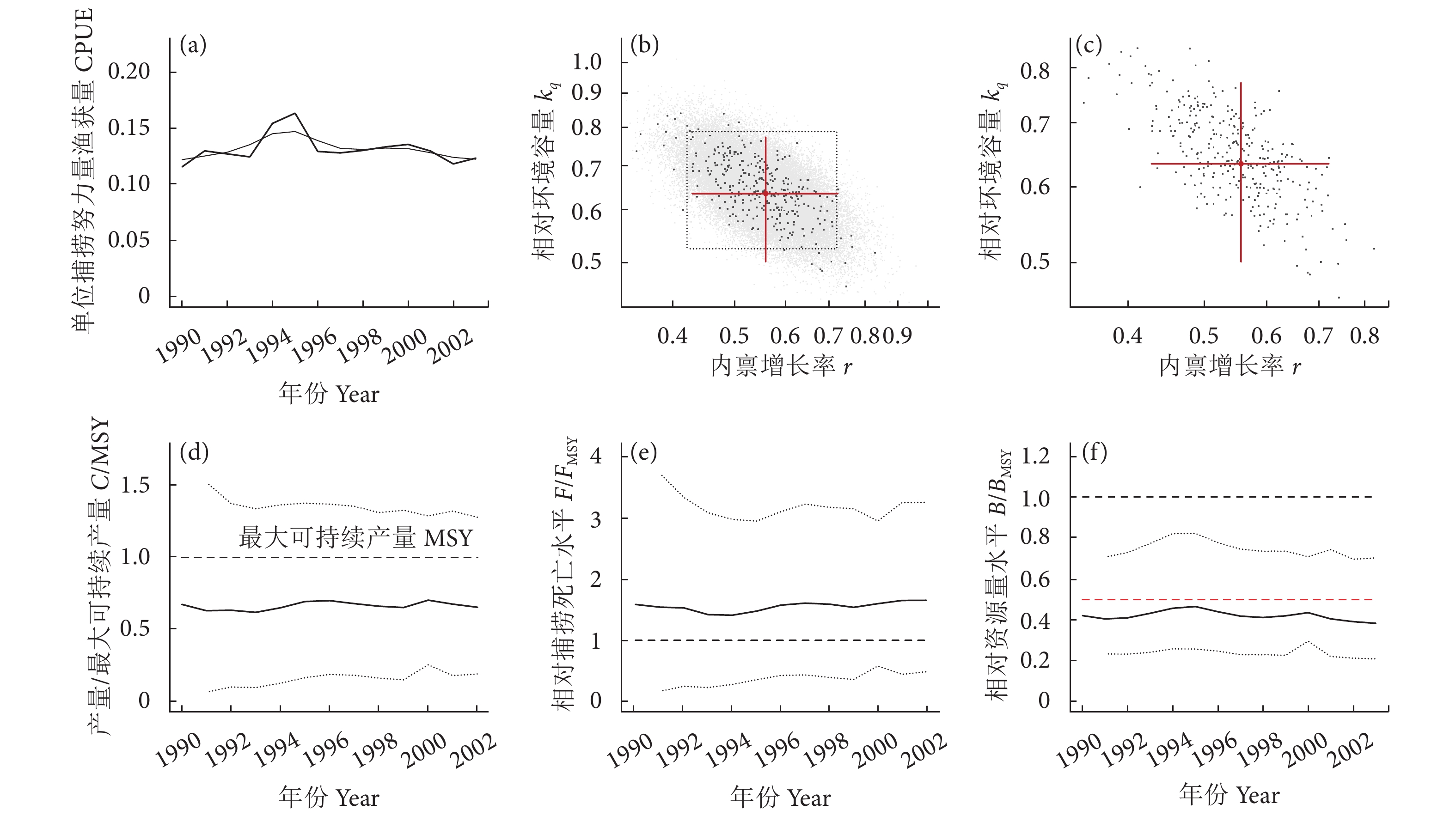
图 3 基于大型底拖网单位捕捞努力量渔获量的日本海带鱼渔业评估结果注：a. 实际 CPUE 数据 (加粗实线) 与平滑后的 CPUE 数据 (灰色实线) 趋势； b. 灰色点表示 AMSY 模型中检验过的所有 r-kq 参数组合，黑色点表示通过 MCMC 过滤器检验的 r-kq 参数组合；c. 放大后的 r-kq 参数组合区域，红色十字星中心为所有参数组合的中值，红色线为95%置信区间；d—f. 加粗实线分别表示 C/MSY、F/FMSY 和 B/BMSY，水平虚线表示 3 个值为 1，虚折线为 95% 置信区间，红色虚线表示在此资源量水平 (B/BMSY<0.5) 之下资源补充会受损。后图同此。Figure 3. Output of AMSY for largehead hairtail fishery in Sea of Japan using CPUE of large bottom trawlNote: a. Trend between actual CPUE data (With thick solid line) and smoothed CPUE data (With gray solid line); b. The cloud of light grey dots indicates the r-kq pairs that were tested by AMSY. The black dots represent viable r-kq pairs that passed the MCMC filters; c. The magnified area was occupied by the viable r-kq pairs. The red cross indicates the most likely r-kq pair at its center as median of the cloud of black dots, with approximate 95% confidence limits in log space; d—f. The bold curves show a time series of the median relative catch (C/MSY), fishing pressure (F/FMSY), and relative stock size (B/BMSY) predicted by AMSY, respectively. The dotted curves are the approximate 95% confidence limits. The dashed red line indicates the stock size below which recruitment (B/BMSY<0.5) may be impaired. The same case in the following figures.表 1 日本海和东海带鱼渔业参数评估结果Table 1. Estimated results of fisheries parameters for largehead hairtail in Sea of Japan and East China Sea参数
Parameter日本海大型
底拖网带鱼渔业
Large bottom trawl
fishery of largehead
hairtail in
Sea of Japan日本海近岸小型
底拖网带鱼渔业
Offshore bottom
trawl fishery of largehead
hairtail in Sea
of Japan基于机动渔船总CPUE的
东海带鱼渔业
Largehead hairtail
fishery in East
China Sea based on
total CPUE of motorized
fishing vessels基于双拖监测CPUE的
东海带鱼渔业
Largehead hairtail
fishery in East
China Sea based on
CPUE of pair-trawler相对环境容量 kq 39.0 (33.5, 45.9) 22.4 (18.8, 26.9) 0.632 (0.514, 0.765) 0.493 (0.325, 0.718) 最大可持续产量 MSYq 5.57 (4.53, 6.81) 3.18 (2.60, 3.94) 0.0895 (0.0696, 0.111) 0.0662 (0.0469, 0.0924) 内禀增长率 r 0.572 (0.449, 0.712) 0.566 (0.450, 0.728) 0.566 (0.443, 0.730) 0.537 (0.413, 0.691) MSY水平下的捕捞死亡系数 FMSY 0.286 (0.224, 0.356) 0.283 (0.225, 0.364) 0.283 (0.221, 0.365) 0.269 (0.206, 0.345) 2000年产量与最大可持续产量比值 C2000/MSY 0.990 (0.596, 1.51) 0.589 (0.261, 1.06) 0.696 (0.257, 1.26) 0.837 2000年相对捕捞死亡水平 F2000/FMSY 2.68 (1.38, 3.92) 1.34 (0.610, 2.56) 1.58 (0.680, 3.22) 1.53 2000年相对资源量 B2000/BMSY 0.370 (0.261, 0.533) 0.440 (0.362, 0.701) 0.442 (0.323, 0.712) 0.546 注：参数评估结果为中值，括号内数字为该参数的95%置信区间。
Note: The estimated parameters are presented as the median values, and the numbers in the brackets are the 95% confidence intervals.基于近岸小型底拖网CPUE评估的日本海带鱼渔业结果 (图4) 显示，虽然1981—2009年产量一直在MSY以下 (图4-d)，但是F一直高于FMSY (图4-e) 而资源量B一直低于BMSY，并且B/BMSY在大部分时间里一直在0.5以内 (图4-f)。评估的参数r为0.566，FMSY为0.283，2000年的C/MSY、F/FMSY和B/BMSY分别为0.589、1.34和0.44 (表1)。
![]()
图 4 基于近岸小型底拖网单位捕捞努力量渔获量的日本海带鱼渔业评估结果Figure 4. Output of AMSY for largehead hairtail fishery in Sea of Japan using CPUE of offshore bottom trawl2.2 东海带鱼渔业
基于机动渔船总CPUE的东海带鱼渔业评估结果 (图5) 显示，1990—2003年带鱼产量一直在MSY之下，F/FMSY和B/BMSY处于较平稳的状态，评估值分别介于1.41~1.67和0.388~0.463。评估的参数r为0.566，FMSY为0.283，2000年的C/MSY、F/FMSY和B/BMSY分别为0.696、1.58和0.442 (表1)。
![]()
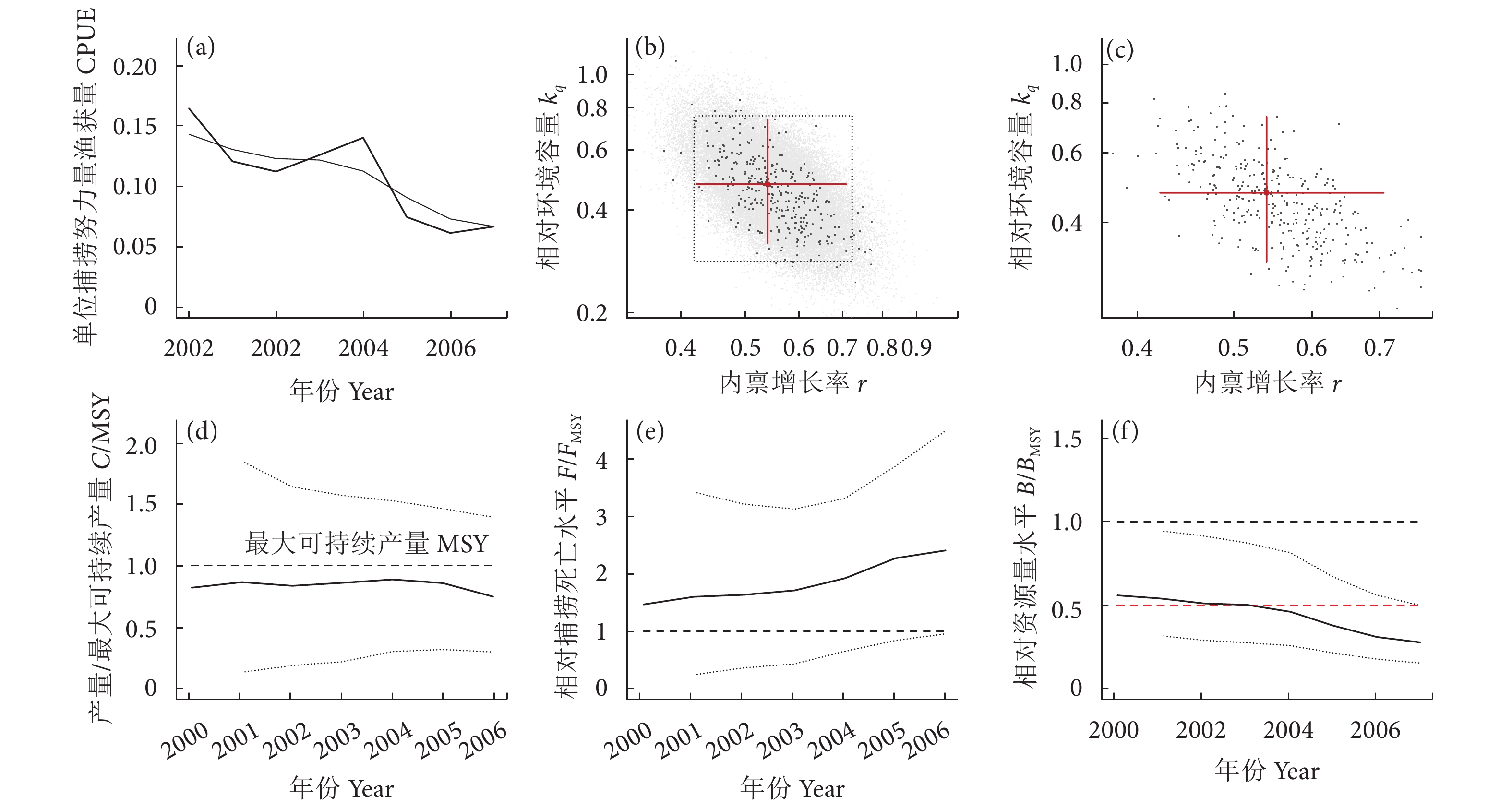
图 5 基于机动渔船总单位捕捞努力量渔获量的东海带鱼渔业评估结果Figure 5. Output of AMSY for largehead hairtail fishery in East China Sea using CPUE of total motorized fishing vessels基于双拖监测CPUE的东海带鱼渔业评估结果 (图6) 显示，2000—2007年带鱼产量一直在MSY之下，F/FMSY处于上升趋势，评估值介于1.49~2.4，而B/BMSY处于下降趋势，评估值介于0.27~0.549。评估的参数r值为0.537，FMSY为0.269，2000年的C/MSY、F/FMSY和B/BMSY分别为0.837、1.53和0.546 (表1)。
![]()
图 6 基于双拖监测单位捕捞努力量渔获量的东海带鱼渔业评估结果Figure 6. Output of AMSY for largehead hairtail fishery in East China Sea using CPUE of pair-trawler2.3 敏感性分析
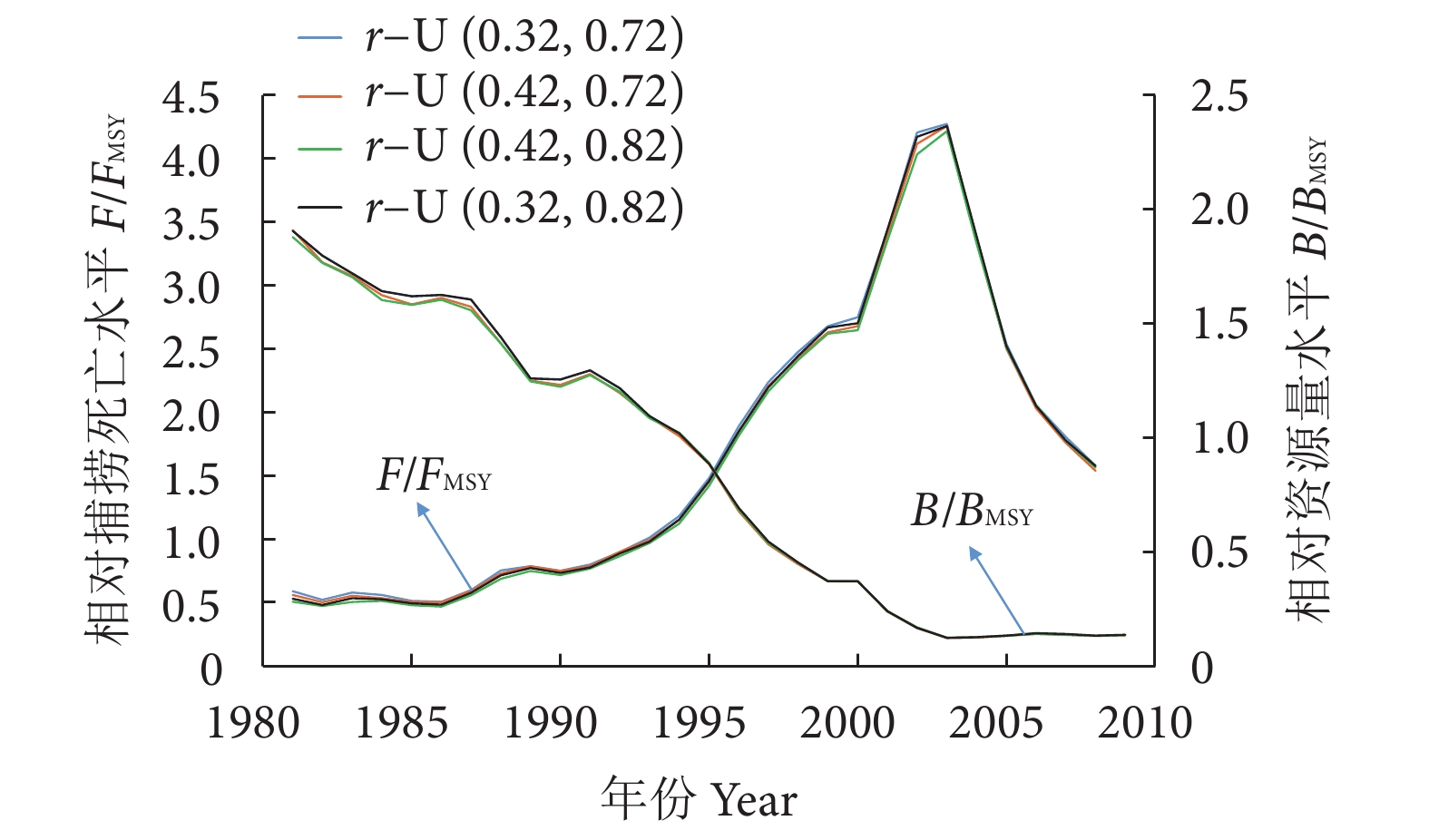
4组在不同r先验分布条件下，日本海大型底拖网带鱼渔业评估序列末年的C/MSY、B/BMSY和F/FMSY评估结果相差不大，但是MSYq、r和FMSY等参数有较明显的差异 (表2)。AMSY模型评估的1981—2009年B/BMSY和F/FMSY趋势较为一致 (图7)。
表 2 日本海大型底拖网带鱼渔业参数在不同r先验分布条件下的评估结果Table 2. Estimated results of fisheries parameters for large bottom trawl largehead hairtail fishery in Sea of Japan under different r prior distributions参数
Parameterr−U (0.32, 0.72) r−U (0.42, 0.72) r−U (0.42, 0.82) r−U (0.32, 0.82) 相对环境容量 kq 38.3 (33.0, 45.8) 39.0 (33.5, 45.9) 38.9 (33.6, 46.3) 38.4 (33.2, 45.7) 最大可持续产量 MSYq 5.14 (3.82, 7.10) 5.57 (4.53, 6.81) 6.08 (4.75, 7.96) 5.56 (4.07, 7.94) 内禀增长率 r 0.537 (0.385, 0.745) 0.572 (0.449, 0.712) 0.626 (0.480, 0.824) 0.579 (0.408, 0.846) MSY水平下的捕捞死亡系数 FMSY 0.269 (0.192, 0.373) 0.286 (0.224, 0.356) 0.313 (0.240, 0.412) 0.290 (0.204, 0.432) 2008年产量与最大可持续产量比值 C2008/MSY 0.211 (0.102, 0.497) 0.208 (0.104, 0.488) 0.206 (0.103, 0.490) 0.210 (0.096, 0.502) 2008年相对捕捞死亡水平 F2008/FMSY 1.58 (0.480, 3.27) 1.56 (0.552, 3.07) 1.56 (0.563, 3.06) 1.58 (0.488, 3.22) 2009年相对资源量 B2009/BMSY 0.136 (0.0762, 0.241) 0.135 (0.0751, 0.246) 0.135 (0.0748, 0.241) 0.136 (0.261, 0.533) ![]()
图 7 日本海大型底拖网带鱼渔业F/FMSY和B/BMSY在不同r先验分布条件下的评估结果Figure 7. Estimated F/FMSY and B/BMSY for large bottom trawl largehead hairtail fishery in Sea of Japan under different r prior distributions4组不同B2000/k先验分布条件下，AMSY模型评估的日本海大型底拖网带鱼渔业MSYq、r和FMSY等参数无明显差异，这一结果与不同r先验分布条件下的评估结果相反 (表3)。评估的1981—2009年的B/BMSY和F/FMSY趋势明显分为了两组，先验分布U (0.05, 0.4) 和U (0.05, 0.5) 的评估结果较一致，而U (0.15, 0.4) 和U (0.15, 0.5) 的评估结果较一致 (图8)。
表 3 日本海大型底拖网带鱼渔业参数在不同B2000/k先验分布条件下的评估结果Table 3. Estimated results of fisheries parameters for large bottom trawl largehead hairtail fishery in Sea of Japan under different B2000/k prior distributions参数
ParameterB2000/k−U (0.05, 0.4) B2000/k−U (0.15, 0.4) B2000/k−U (0.15, 0.5) B2000/k−U (0.05, 0.5) 相对环境容量 kq 40.5 (34.1, 49.2) 39.0 (33.5, 45.9) 38.8 (33.5, 46.6) 39.7 (33.9, 48.1) 最大可持续产量 MSYq 5.66 (4.62, 6.94) 5.57 (4.53, 6.81) 5.56 (4.50, 6.93) 5.65 (4.58, 6.81) 内禀增长率 r 0.560 (0.439, 0.697) 0.572 (0.449, 0.712) 0.573 (0.449, 0.726) 0.569 (0.443, 0.706) MSY水平下的捕捞死亡系数 FMSY 0.280 (0.219, 0.349) 0.286 (0.224, 0.356) 0.287 (0.224, 0.363) 0.285 (0.221, 0.353) 2008年产量与最大可持续产量比值 C2008/MSY 0.189 (0.098, 0.473) 0.208 (0.104, 0.488) 0.203 (0.099, 0.491) 0.193 (0.092, 0.502) 2008年相对捕捞死亡水平 F2008/FMSY 1.50 (0.473, 3.090) 1.56 (0.552, 3.07) 1.54 (0.518, 3.17) 1.50 (0.471, 3.07) 2009年相对资源量 B2009/BMSY 0.129 (0.0717, 0.236) 0.135 (0.0751, 0.246) 0.135 (0.0737, 0.243) 0.132 (0.0733, 0.239) ![]()
图 8 日本海大型底拖网带鱼渔业参数在不同B2000/k先验分布条件下的评估结果Figure 8. Estimated F/FMSY and B/BMSY for large bottom trawl largehead hairtail fishery in Sea of Japan under different B2000/k prior distributions3. 讨论
本研究首次尝试利用资源丰度指数和恢复力先验信息对日本海和东海带鱼渔业进行资源评估，结果显示2个海域的带鱼渔业在20世纪90年代至21世纪00年代的大部分时间里B/BMSY低于1，而F/FMSY高于1，处于过度捕捞状态，建议控制捕捞产量且执行最小可捕规格，以恢复其亲体生物量。AMSY模型里MSYq和FMSY等参数评估结果对不同r先验分布范围比较敏感，而B/BMSY和F/FMSY等生物学参考点评估结果对不同Bt/k先验分布范围的下限设置比较敏感。以上研究结果可为日本海和东海带鱼渔业管理和AMSY模型在我国近海重点海域的应用提供参考。
由于带鱼的高经济价值和产量，一直以来都被认为是我国东海渔业资源状况的风向标[17]，也是日本海的重要经济鱼种[19]。已有学者通过不同的渔业资源评估模型对带鱼渔业进行了资源评估，评估方法包括Catch-MSY模型[9]、贝叶斯状态空间模型[18]、非平衡剩余产量模型[20]和Beverton-Holt 模型[21]等。带鱼的过度捕捞已成为一个不争的事实，渔获量和渔获率均下降明显[22]，渔获年龄组成由20世纪50—60年代的0~7龄变为20世纪90年代后的0~4龄[21]，3龄及以上占比已由20世纪50年代的6.11%下降到21世纪00年代的0.58%[21]。利用基于产量统计数据的渔业资源评估模型[9,18,20]对东海带鱼评估的结果显示，该渔业在20世纪90年代和21世纪00年代的捕捞产量在MSY之上，F/FMSY在2000—2006年大于1，随着近年来产量下降而下降，但B/BMSY大部分年份高于1[18]，这与本文的结果有较大出入，原因在于基于产量的评估模型高度依赖统计产量数据的准确性[23]。东海带鱼产量自20世纪70年代便超过40万t，2000年更是超过90万t，近年来虽有所下降但仍在高位[9]。产量一直较高使得剩余产量模型等基于产量的评估模型默认该渔业可以承受较高的捕捞强度，产生了较高的MSY评估结果，造成了F/FMSY和B/BMSY等生物学参考点评估结果的误差。带鱼渔业产量在20世纪70—80年代已出现一次明显的下降[9]，20世纪80年代末期至21世纪00年代初期的快速增长，是因为渔船大功率钢质化步伐明显加快，作业渔场由沿岸和近海逐渐向外海转移[22]。近年来，大量0~1龄带鱼幼鱼被捕获[21]，这部分产量不应该被捕获并统计在产量之中，另外，包括我国近海在内的世界各海域均存在统计产量失真的情况[23]，也会对评估结果造成一定的影响。
联合国海洋法公约要求其签署的国家和地区在MSY框架下管理鱼类和无脊椎动物的开发，使其种群生物量必须高于MSY水平下的生物量(BMSY)，而F需要低于MSY水平下的捕捞死亡系数 (FMSY)[7]。由于数据缺乏，我国近海只有少数大宗鱼类种群如带鱼[18]、小黄鱼 (Larimichthys polyactis)[9]和鲐 (Scomber japonicus)[24]等存在该框架下的资源评估，而且大部分评估均基于统计产量进行。随着我国对海洋渔业资源保护的重视，国务院发布了《关于促进海洋渔业持续健康发展的若干意见》(国发〔2013〕11号)，强调了渔业资源调查的重要性并要求“每五年开展一次渔业资源全面调查，常年开展监测和评估，重点调查濒危物种、水产种质等重要渔业资源和经济生物产卵场、江河入海口、南海等重要渔业水域”。通过标准化的科学调查所得到的CPUE数据是一个良好的资源丰度指标[25]，近年来开展的重点海域连续调查监测为AMSY模型在我国的应用提供了数据基础。该模型除了需要CPUE数据外，还需要r和特定年份的相对资源量 (Bt/k) 这2个参数的先验分布。其中，r也是基于产量的评估模型如CMSY、Catch-MSY等所需参数，通常利用评估对象的繁殖力、最大年龄和性成熟年龄等生物学参数来设定[8]，也可以根据每个种群已有参数的经验公式来设置[9]。Froese等[7]推荐参数Bt/k的设置根据相应年份的体长频率分布数据、通过LBB模型来评估，由于带鱼渔业已有相应的研究，笔者采用了4个CPUE序列均有的2000年Bt/k评估结果[9,18]。敏感性分析表明，不同先验分布范围的2个参数对AMSY评估的参数和结果均有影响，尤其要谨慎设置参数Bt/k的分布范围下限，因其会对F/FMSY和B/BMSY等生物学参考点的评估结果产生较大影响 (图8)。
综上所述，基于CPUE数据的AMSY模型是一种较适合我国近海的渔业资源评估方法，尤其是缺乏统计产量数据的重点河口和海湾。但数据有限条件下的渔业资源评估方法都是不得已而为之的“下策”，在实际渔业资源评估和管理中，一方面需要尽可能地收集评估对象的数据，利用不同评估方法来佐证评估结果，另一方面需要参照可靠的评估结果和依据来设定关键参数 (如r和Bt/k) 的分布范围。
致谢：感谢德国基尔亥姆霍兹海洋研究中心Rainer Froese高级研究员以及希腊塞萨洛尼基亚里士多德大学Athanassios C. Tsikliras博士在模型使用过程中给予的指导和帮助！
-
![]()
图 1 1981—2009 年日本海带鱼大型底拖网和近岸底拖网渔业单位捕捞努力量渔获量
Figure 1. CPUE of largehead hairtail fisheries by large bottom trawl and offshore bottom trawl in Sea of Japan from 1981 to 2009
![]()
图 2 东海带鱼渔业单位捕捞努力量渔获量
Figure 2. CPUE of largehead hairtail by marine motorized fishing vessels and pair-trawler in East China Sea
![]()
图 3 基于大型底拖网单位捕捞努力量渔获量的日本海带鱼渔业评估结果
注：a. 实际 CPUE 数据 (加粗实线) 与平滑后的 CPUE 数据 (灰色实线) 趋势； b. 灰色点表示 AMSY 模型中检验过的所有 r-kq 参数组合，黑色点表示通过 MCMC 过滤器检验的 r-kq 参数组合；c. 放大后的 r-kq 参数组合区域，红色十字星中心为所有参数组合的中值，红色线为95%置信区间；d—f. 加粗实线分别表示 C/MSY、F/FMSY 和 B/BMSY，水平虚线表示 3 个值为 1，虚折线为 95% 置信区间，红色虚线表示在此资源量水平 (B/BMSY<0.5) 之下资源补充会受损。后图同此。
Figure 3. Output of AMSY for largehead hairtail fishery in Sea of Japan using CPUE of large bottom trawl
Note: a. Trend between actual CPUE data (With thick solid line) and smoothed CPUE data (With gray solid line); b. The cloud of light grey dots indicates the r-kq pairs that were tested by AMSY. The black dots represent viable r-kq pairs that passed the MCMC filters; c. The magnified area was occupied by the viable r-kq pairs. The red cross indicates the most likely r-kq pair at its center as median of the cloud of black dots, with approximate 95% confidence limits in log space; d—f. The bold curves show a time series of the median relative catch (C/MSY), fishing pressure (F/FMSY), and relative stock size (B/BMSY) predicted by AMSY, respectively. The dotted curves are the approximate 95% confidence limits. The dashed red line indicates the stock size below which recruitment (B/BMSY<0.5) may be impaired. The same case in the following figures.
![]()
图 4 基于近岸小型底拖网单位捕捞努力量渔获量的日本海带鱼渔业评估结果
Figure 4. Output of AMSY for largehead hairtail fishery in Sea of Japan using CPUE of offshore bottom trawl
![]()
图 5 基于机动渔船总单位捕捞努力量渔获量的东海带鱼渔业评估结果
Figure 5. Output of AMSY for largehead hairtail fishery in East China Sea using CPUE of total motorized fishing vessels
![]()
图 6 基于双拖监测单位捕捞努力量渔获量的东海带鱼渔业评估结果
Figure 6. Output of AMSY for largehead hairtail fishery in East China Sea using CPUE of pair-trawler
![]()
图 7 日本海大型底拖网带鱼渔业F/FMSY和B/BMSY在不同r先验分布条件下的评估结果
Figure 7. Estimated F/FMSY and B/BMSY for large bottom trawl largehead hairtail fishery in Sea of Japan under different r prior distributions
![]()
图 8 日本海大型底拖网带鱼渔业参数在不同B2000/k先验分布条件下的评估结果
Figure 8. Estimated F/FMSY and B/BMSY for large bottom trawl largehead hairtail fishery in Sea of Japan under different B2000/k prior distributions
表 1 日本海和东海带鱼渔业参数评估结果
Table 1 Estimated results of fisheries parameters for largehead hairtail in Sea of Japan and East China Sea
参数
Parameter日本海大型
底拖网带鱼渔业
Large bottom trawl
fishery of largehead
hairtail in
Sea of Japan日本海近岸小型
底拖网带鱼渔业
Offshore bottom
trawl fishery of largehead
hairtail in Sea
of Japan基于机动渔船总CPUE的
东海带鱼渔业
Largehead hairtail
fishery in East
China Sea based on
total CPUE of motorized
fishing vessels基于双拖监测CPUE的
东海带鱼渔业
Largehead hairtail
fishery in East
China Sea based on
CPUE of pair-trawler相对环境容量 kq 39.0 (33.5, 45.9) 22.4 (18.8, 26.9) 0.632 (0.514, 0.765) 0.493 (0.325, 0.718) 最大可持续产量 MSYq 5.57 (4.53, 6.81) 3.18 (2.60, 3.94) 0.0895 (0.0696, 0.111) 0.0662 (0.0469, 0.0924) 内禀增长率 r 0.572 (0.449, 0.712) 0.566 (0.450, 0.728) 0.566 (0.443, 0.730) 0.537 (0.413, 0.691) MSY水平下的捕捞死亡系数 FMSY 0.286 (0.224, 0.356) 0.283 (0.225, 0.364) 0.283 (0.221, 0.365) 0.269 (0.206, 0.345) 2000年产量与最大可持续产量比值 C2000/MSY 0.990 (0.596, 1.51) 0.589 (0.261, 1.06) 0.696 (0.257, 1.26) 0.837 2000年相对捕捞死亡水平 F2000/FMSY 2.68 (1.38, 3.92) 1.34 (0.610, 2.56) 1.58 (0.680, 3.22) 1.53 2000年相对资源量 B2000/BMSY 0.370 (0.261, 0.533) 0.440 (0.362, 0.701) 0.442 (0.323, 0.712) 0.546 注：参数评估结果为中值，括号内数字为该参数的95%置信区间。
Note: The estimated parameters are presented as the median values, and the numbers in the brackets are the 95% confidence intervals.
下载: 导出CSV
表 2 日本海大型底拖网带鱼渔业参数在不同r先验分布条件下的评估结果
Table 2 Estimated results of fisheries parameters for large bottom trawl largehead hairtail fishery in Sea of Japan under different r prior distributions
参数
Parameterr−U (0.32, 0.72) r−U (0.42, 0.72) r−U (0.42, 0.82) r−U (0.32, 0.82) 相对环境容量 kq 38.3 (33.0, 45.8) 39.0 (33.5, 45.9) 38.9 (33.6, 46.3) 38.4 (33.2, 45.7) 最大可持续产量 MSYq 5.14 (3.82, 7.10) 5.57 (4.53, 6.81) 6.08 (4.75, 7.96) 5.56 (4.07, 7.94) 内禀增长率 r 0.537 (0.385, 0.745) 0.572 (0.449, 0.712) 0.626 (0.480, 0.824) 0.579 (0.408, 0.846) MSY水平下的捕捞死亡系数 FMSY 0.269 (0.192, 0.373) 0.286 (0.224, 0.356) 0.313 (0.240, 0.412) 0.290 (0.204, 0.432) 2008年产量与最大可持续产量比值 C2008/MSY 0.211 (0.102, 0.497) 0.208 (0.104, 0.488) 0.206 (0.103, 0.490) 0.210 (0.096, 0.502) 2008年相对捕捞死亡水平 F2008/FMSY 1.58 (0.480, 3.27) 1.56 (0.552, 3.07) 1.56 (0.563, 3.06) 1.58 (0.488, 3.22) 2009年相对资源量 B2009/BMSY 0.136 (0.0762, 0.241) 0.135 (0.0751, 0.246) 0.135 (0.0748, 0.241) 0.136 (0.261, 0.533)
下载: 导出CSV
表 3 日本海大型底拖网带鱼渔业参数在不同B2000/k先验分布条件下的评估结果
Table 3 Estimated results of fisheries parameters for large bottom trawl largehead hairtail fishery in Sea of Japan under different B2000/k prior distributions
参数
ParameterB2000/k−U (0.05, 0.4) B2000/k−U (0.15, 0.4) B2000/k−U (0.15, 0.5) B2000/k−U (0.05, 0.5) 相对环境容量 kq 40.5 (34.1, 49.2) 39.0 (33.5, 45.9) 38.8 (33.5, 46.6) 39.7 (33.9, 48.1) 最大可持续产量 MSYq 5.66 (4.62, 6.94) 5.57 (4.53, 6.81) 5.56 (4.50, 6.93) 5.65 (4.58, 6.81) 内禀增长率 r 0.560 (0.439, 0.697) 0.572 (0.449, 0.712) 0.573 (0.449, 0.726) 0.569 (0.443, 0.706) MSY水平下的捕捞死亡系数 FMSY 0.280 (0.219, 0.349) 0.286 (0.224, 0.356) 0.287 (0.224, 0.363) 0.285 (0.221, 0.353) 2008年产量与最大可持续产量比值 C2008/MSY 0.189 (0.098, 0.473) 0.208 (0.104, 0.488) 0.203 (0.099, 0.491) 0.193 (0.092, 0.502) 2008年相对捕捞死亡水平 F2008/FMSY 1.50 (0.473, 3.090) 1.56 (0.552, 3.07) 1.54 (0.518, 3.17) 1.50 (0.471, 3.07) 2009年相对资源量 B2009/BMSY 0.129 (0.0717, 0.236) 0.135 (0.0751, 0.246) 0.135 (0.0737, 0.243) 0.132 (0.0733, 0.239)
下载: 导出CSV
-
[1] PAULY D, ZELLER D. Catch reconstructions reveal that global marine fisheries catches are higher than reported and declining[J]. Nat Commun, 2016, 7: 10244. doi: 10.1038/ncomms10244
[2] KLEISNER K, ZELLER D, FROESE R, et al. Using global catch data for inferences on the world's marine fisheries[J]. Fish Fish, 2013, 14(3): 293-311. doi: 10.1111/j.1467-2979.2012.00469.x
[3] MAUNDER M N, PUNT A E. A review of integrated analysis in fisheries stock assessment[J]. Fish Res, 2013, 142: 61-74. doi: 10.1016/j.fishres.2012.07.025
[4] COSTELLO C, OVANDO D, HILBORN R, et al. Status and solutions for the world's unassessed fisheries[J]. Science, 2012, 338(6106): 517-520. doi: 10.1126/science.1223389
[5] FROESE R, DEMIREL N, CORO G, et al. Estimating fisheries reference points from catch and resilience[J]. Fish Fish, 2017, 18: 506-526. doi: 10.1111/faf.12190
[6] FROESE R, WINKER H, CORO G, et al. A new approach for estimating stock status from length frequency data[J]. ICES J Mar Sci, 2018, 75(6): 2004-2015. doi: 10.1093/icesjms/fsy078
[7] FROESE R, WINKER H, CORO G, et al. Estimating stock status from relative abundance and resilience[J]. ICES J Mar Sci, 2020, 77(2): 527-538. doi: 10.1093/icesjms/fsz230
[8] 张魁, 廖宝超, 许友伟, 等. 基于渔业统计数据的南海区渔业资源可捕量评估[J]. 海洋学报, 2017, 39(8): 25-33. [9] ZHANG K, ZHANG J, XU Y, et al. Application of a catch-based method for stock assessment of three important fisheries in the East China Sea[J]. Acta Oceanol Sin, 2018, 37(2): 102-109. doi: 10.1007/s13131-018-1173-9
[10] JI Y, LIU Q, LIAO B, et al. Estimating biological reference points for largehead hairtail (Trichiurus lepturus) fishery in the Yellow Sea and Bohai Sea[J]. Acta Oceanol Sin, 2019, 38(10): 20-26. doi: 10.1007/s13131-019-1343-4
[11] WANG X, QIU Y, DU F, et al. Population parameters and dynamic pool models of commercial fishes in the Beibu Gulf, northern South China Sea[J]. Chin J Oceanol Limn, 2012, 30(1): 102-117.
[12] 王淼娣, 王雪辉, 孙典荣, 等. 基于长度贝叶斯生物量估算法评估北部湾大头白姑鱼资源状况[J]. 南方水产科学, 2021, 17(2): 20-27. doi: 10.12131/20200202 [13] ZHANG L, REN Q, LIU M, et al. Fishery stock assessments in the Min River Estuary and Its adjacent waters in Southern China using the Length-Based Bayesian Estimation (LBB) method[J]. Front Mar Sci, 2020, 7: 507. doi: 10.3389/fmars.2020.00507
[14] ZHANG K, ZHANG J, SHI D, et al. Assessment of coral reef fish stocks from the Nansha Islands, South China Sea, using length-based Bayesian biomass estimation[J]. Front Mar Sci, 2021, 7: 610707. doi: 10.3389/fmars.2020.610707
[15] 徐兆礼, 陈佳杰. 再议东黄渤海带鱼种群划分问题[J]. 中国水产科学, 2016, 23(5): 1185-1196. [16] 李发凯. 东黄海带鱼资源变动的统计研究[D]. 舟山: 浙江海洋大学, 2016: 9-17. [17] 王垚. 伏季休渔条件下东海带鱼资源评估[D]. 舟山: 浙江海洋学院, 2010: 14-19. [18] 张魁, 陈作志. 应用贝叶斯状态空间建模对东海带鱼的资源评估[J]. 中国水产科学, 2015, 22(5): 1015-1026. [19] KAO W, TOMIYASU M, TAKAHASHI, R, et al. Spatial and temporal distribution of hairtail (Trichiurus japonicus) in the Bungo Channel, Japan[J]. J Mar Acous Soc Jpn, 2015, 42(4): 167-176. doi: 10.3135/jmasj.42.167
[20] WANG Y, LIU Q. Applications of CEDA and ASPIC computer packages to the hairtail (Trichiurus japonicus) fishery in the East China Sea[J]. Chin J Oceanol Limnol, 2013, 31(1): 92-96. doi: 10.1007/s00343-013-2073-7
[21] 凌建忠, 李圣法, 严利平, 等. 基于Beverton-Holt 模型的东海带鱼资源利用与管理[J]. 应用生态学报, 2008, 19(1): 178-182. [22] 王跃中, 贾晓平, 林昭进, 等. 东海带鱼渔获量对捕捞压力和气候变动的响应[J]. 水产学报, 2011, 35(12): 1881-1889. [23] 张魁, 刘群, 廖宝超, 等. 渔业数据失真对两种非平衡剩余产量模型评估结果的影响比较[J]. 水产学报, 2018, 42(9): 1378-1389. [24] 李纲, 陈新军, 官文江. 基于贝叶斯方法的东、黄海鲐资源评估及管理策略风险分析[J]. 水产学报, 2010, 34(5): 740-750. [25] SILLIMAN R P, GUTSELL J S. Experimental exploitation of fish populations[J]. Fish B-NOAA, 1958, 58: 214-252.
-
期刊类型引用(1)
1. 刘尊雷，杨林林，金艳，袁兴伟，张翼，张辉，许敏，程家骅，严利平. 基于CMSY和BSM的东海区重要渔业种类资源评估. 中国水产科学. 2023(06): 735-752 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 900
- HTML全文浏览量: 259
- PDF下载量: 98
- 被引次数: 1
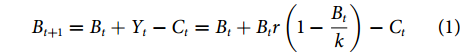
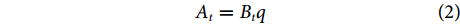
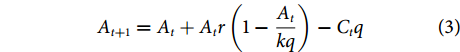
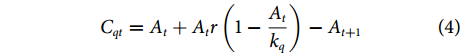
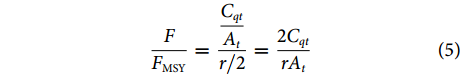
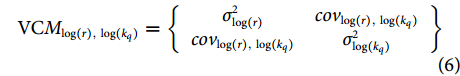
粤公网安备 44010502001741号
