Performance analysis of the column cod-end and truncated cone cod-end of deep-water net cage
-
摘要:
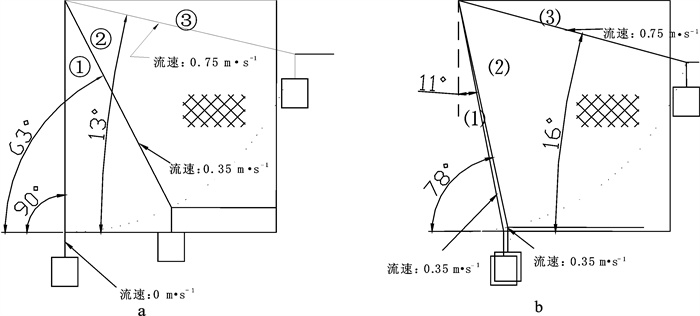
分析比较了网箱圆柱形囊网与圆台形囊网在相同制作材料及同等工况条件下的优缺点,流速在0~0.35 m · s-1区间时,前者在养殖容积、制作工艺、换网操作优于后者;流速在0.35~0.75 m · s-1区间时,后者在养殖容积保持率、制作成本、换网操作优于前者;流速大于0.75 m · s-1时,两者优劣不明显。
Abstract:We tested the relative merits of the column cod-end and truncated cone cod-end of deep-water net cage in the same make materials and under the equal working conditions.Under the condition of flow rate of 0~0.35 m · s-1, the carrying capacity, facture process and change of net clothing operation of the former were superior to those of the latter. While velocity of flow at 0~0.35 m · s-1, the carrying capacity keeping rate, facture cost and change of net clothing operation of the latter were better than those of the former. When flow rate over 0.75 m · s-1, the good and bad of both were not obvious.
-
Keywords:
- net cage /
- cod-end /
- performance /
- analysis
-
网衣系统是深水网箱的主要组成部分,在维持鱼类生长空间、防止鱼类逃逸和敌害侵袭、保持箱体内外水体交换畅通方面起着主导作用,高海况条件下网衣是否安全与可靠直接关系到养殖生产的经济效益和可持续发展。网衣也是网箱系统中受力最为复杂的部件之一,在水流作用下网衣所受到的外力中水流力与网衣的变形具有高度的相互依赖性,即网衣在水流作用下会发生运动变形,而当网衣形状发生变化后,作用在网衣上的水流力也将随之发生变化,这与工程上的一般刚性结构物有着很大的不同,网衣的这些特征正是数值计算时所需要解决的问题。近年来,国内外关于网衣水动力特性的研究已有不少,SUZUKI等[1]和TAKAGI等[2]采用质量弹簧单元的方法模拟了渔网的动力学性能。詹杰民等[3-4]、李玉成和桂福坤[5]、WAN等[6-7]对水流作用下平面网衣的受力进行了研究。LADER和ENERHAUG[8]、LADER和FREDHEIM[9]、HUANG等[10-11]、LI等[12]、ZHAO等[13]及LEE等[14]均采用集中质量法将网衣离散成众多质点进行模拟,结合物理模型试验研究了不同海况条件下圆形网箱的水动力特性。在上述所列文献中,无论是有关平面网衣还是圆形网衣的研究,其内容都是研究网衣达到稳定状态后的水动力特性情况,而对水流作用下网衣达到稳定状态前受力与变形的变化过程研究,目前国内还未见相关报道。
在此之前的研究已分别对平面网衣和圆形网衣的运动变形特性进行了数模研究[15-16],建立了网衣数学模型,并利用前人的试验结果对数学模型进行了验证,结果吻合较好。该研究是在上述研究成果的基础上,基于建立的网衣数学模型,分别对水流作用下网衣所受的水流力、网衣形状和网衣运动位移三者随时间的变化过程进行了数值模拟,旨在探讨和分析网衣在水流作用过程中的动态变化规律。
1. 网衣数学模型
利用集中质量法将柔软的网衣分解成众多质点和构件组成的离散模型,集中质量点设于每个网目目脚的两端(图 1)。在计算作用在目脚上的外力时,可以将单个目脚看作为一个构件,其在水流作用下的受力由重力、浮力、网线张力和水流力组成,具体数学表达式在文献[16]已作详细介绍。
整体坐标系下单个质点的受力情况见图 2,利用牛顿第二定律建立如下的网衣各集中质量点的运动方程。图 2中的T1、T2、T3和T4为网线张力,FD和FI为水流力中的速度力和惯性力。
$$ m_i X_i=\sum\limits_{j=1}^N F_{D X j}+F_{I X j}+T_{x j} $$ (1a) $$ m_i Y_i=\sum\limits_{j=1}^N F_{D Yj}+F_{I Y j}+T_{Y j} $$ (1b) $$ m_i Z_i=\sum\limits_{j=1}^N F_{D Z j}+F_{I Z j}+P_j+T_{Z j} $$ (1c) 式中N为质点相关构件的数量,X、Y和Z为质点的加速度,Pj为重力与浮力的合力。
根据Morison方程,网衣构件上的水流力计算表达式可表示为如下形式,其中等式右边第一项表示网衣构件的速度力,第二项表示水体的附加质量力,第三项表示网衣构件排开水体的惯性力。
$$ \begin{aligned} & F_c=F_D+F_I=\frac{1}{2} \rho_w C_D S\left|\boldsymbol{U}-\boldsymbol{U}_{\mathrm{S}} \cdot \mathbf{e}\right|^2 \mathbf{e}+ \\ & \rho_w V_0 C_M \frac{5 \boldsymbol{U}}{5 t}-\rho_w V_0 k_m \frac{5 \boldsymbol{U}_S}{5 t} \end{aligned} $$ (2) 式中US为构件自身速度,CD为速度力系数,CM=1+km为惯性力系数,km为附加质量系数,V0为构件体积,e为构件单位向量。
由于网衣运动方程(1)属于下述形式的二阶微分方程,可以利用四阶Runge-Kutta方法进行数值求解[17],相关数学表达式为:
$$ \xi=F t, \xi \xi $$ (3) 质点的位移ξ和速度ξ可以表达为:
$$ \begin{aligned} & \xi t+\Delta t=\xi t+\Delta t \cdot \xi(t)+\Delta t^2 \cdot\left(k_1+k_2+\right. \\ & \left.k_3\right) /6 \end{aligned} $$ (4a) $$ \xi t+\Delta t=\xi^{\prime} t+\Delta t \cdot \quad k_1+2 k_2+2 k_3+k_4 \\ /6 $$ (4b) 式中k1、k2、k3和k4分别为:
$$ k_1=F t, \xi t, \xi t $$ $$ k_2=F t+\frac{\Delta t}{2}, \xi t+\frac{\Delta t}{2} \xi t, \xi t+\frac{\Delta t}{2} k_1 $$ $$ k_3=F t+\frac{\Delta t}{2}, \xi t+\frac{\Delta t}{2} \xi t+\frac{\Delta t^2}{4} k_1, \xi t+\frac{\Delta t}{2} k_2 $$ $$ k_1=F t+\Delta t, \xi t+\Delta t \xi_t+\frac{\Delta t^2}{2} k_2, \xi t+\Delta t k_3 $$ 网衣的配重采用底框设计,目的是减少网衣的变形。该文基于集中质量点法将底框离散成众多微元构件,并将底框视为刚体处理。在运动分析时将各个微元构件所受到的外力合力累加到底框的质心处,相当于只对一个质点建立6个自由度上的运动方程,从而简化了计算。有关底框具体的数学方程可参考文献[18],这里不作详细叙述。
2. 数学模型的验证
关于网衣数学模型的正确性和有效性的验证,黄小华等[16]已针对LADER和ENERHAUG[8]的网衣试验情况进行了数值模拟,给出了各种流速下网衣所受的水流力和网衣容积损失率的计算结果(表 1)。结果表明,在各种不同的流速条件下,网衣受力与变形的计算结果与试验结果十分接近,误差值基本上都在10%以内。
表 1 不同流速条件下的计算和试验结果比较Table 1. Comparison of calculated and experimental results under different current velocities流速/m·s-1
velocity容积损失率/% volume reduction rate 水流力/N drag force 试验值
experimental value计算值
calculated value绝对误差
absolute error试验值
experimental value计算值
calculated value相对误差/%
relative error0.13 1 1 0 12.02 12.14 1 0.21 5 4 1 21.97 23.97 9 0.26 11 8 3 34.96 35.37 1 0.33 24 19 5 49.79 44.39 11 0.52 36 34 2 88.01 82.03 7 3. 计算参数的选取
圆柱形网衣初始形状如图 3所示,网衣顶端固定,网衣底端处设有一根长为40 m的金属钢圈作为配重。网衣周长40 m,高度9.6 m,网目大小2a=75 mm,网线直径d=3 mm,网衣材质为PE(ρ=953kg · m-3),横向网目数为896目,缩结系数0.6;纵向网目数为160目,缩结系数0.8。在数值计算中,水流方向为x方向,海水的密度ρw=1 030 kg · m-3,重力加速度g=9.81m · s-2,附加质量系数km=1.0。配重大小为GW1=400 kg与GW2=800 kg 2种,水流速度取U=0.3 m · s-1、0.4 m · s-1、0.5 m · s-1和0.6 m · s-1。
由于计算中的网衣结点数太多(287 616个),笔者采用网目群化方法[19-20]将相邻16×16个网目合并为1个等效大网目(结点总数减少到1 176个),以减少计算时间提高计算效率。
4. 计算结果及分析
4.1 网衣变形
图 4给出了配重GW1、U=0.4 m · s-1时网衣稳定前不同时刻的动态变形情况。可以很明显地看出网衣在运动开始阶段(t<5 s)变形很快,随着水流作用时间的延长,底框倾角从水平开始逐渐增加,网衣在底框以及网线张力的作用下变形幅度逐渐减慢,网衣各结点运动速度减小,并最终在t=50 s时因受力平衡达到稳定状态后而停止运动。
图 5和表 2为不同配重和流速条件下网衣达到稳定状态后的变形模拟结果。可以直观地看出流速增加会加剧网衣的变形。以配重GW1为例,当流速U=0.3 m · s-1时网衣容积损失率较小(14%),流速U=0.6 m · s-1时网箱容积损失率高达41%,后者约为前者的3倍。当网衣底端配重增加到800 kg时网衣容积损失率减小,变形改善明显。在流速U=0.6 m · s-1时和增加配重后,容积损失率减少了16%,表明了配重及流速大小对网衣变形具有显著影响。
4.2 水流力
图 6为水流作用下网衣所受水流力的变化历时曲线,实线代表配重GW1下的计算值,虚线代表配重GW2下的计算值。从图 6可以看出,在水流作用网衣的初始阶段,水流力呈现先减小后增加的变化趋势,随着水流作用时间的延长,水流力的震荡幅度越来越小,水流力的历时曲线近乎一条平行于横坐标轴的直线。其原因主要是因为水流力的大小与网衣构件速度密切相关,并和它具有一定的反比关系,当网衣离开t=0 s时刻的初始位置而发生运动时,水流的冲击作用能使网衣的运动速度在短时间内迅速达到最大,这时网衣所受水流力最小,随后在配重系统的影响和网线张力逐渐增加的情况下,网衣的运动速度会逐渐减小直至网衣达到一个相对稳定的状态。
比较不同配重和流速条件下水流力的计算结果(表 2)可以发现,配重或流速的增加都会使得网衣所受水流力作用加大,表明了配重及流速大小对网衣受力同样具有显著影响。
表 2 网衣稳定后的水流力和容积损失率计算值Table 2. Calculated results of drag force and volume reduction rate流速/m·s-1
velocity水流力/kN drag force 容积损失率volume reduction rate GW1 GW2 GW1 GW2 0.3 4.04 5.64 14% 8% 0.4 5.72 7.98 23% 13% 0.5 7.49 10.01 32% 19% 0.6 8.87 12.54 41% 25% 4.3 网衣底端位移
图 7为网衣底端中心点坐标的历时曲线。可以看出,在水流作用网衣过程中网衣底端中心点的水平和垂向坐标值都随着时间的递增而缓慢增加,直至网衣稳定时达到最大。当增加流速时网衣底端的水平和垂向坐标值都增加。配重GW1条件下,流速U=0.3 m · s-1时水平坐标最大值为2.04 m,垂向坐标最大值为-8.42 m;流速U=0.6 m · s-1时水平坐标最大值为4.2 m,垂向坐标最大值为-5.72 m,后者分别增加2.16 m和2.7 m。对于不同流速,当配重增加时网衣底端的水平和垂向坐标值都显著减小。
5. 结语
该文基于建立的网衣数学模型对圆型网衣的动态变化过程进行了数模研究,给出了不同条件下网衣所受的水流力、网衣动态变形以及网衣底端特定点位移的计算结果。可以发现,在水流作用网衣的初始阶段,网衣变形较快,所受的水流力呈现出先减小后增加的变化趋势,随着水流作用时间的延长,网衣的受力、变形和运动都能达到一个稳定的状态。水流速度增加会加剧网衣的运动变形,且使网衣所受的水流力增加;当网衣底端配重增加时,网衣的运动变形会显著减小,但网衣所受的水流力将明显增加。
-
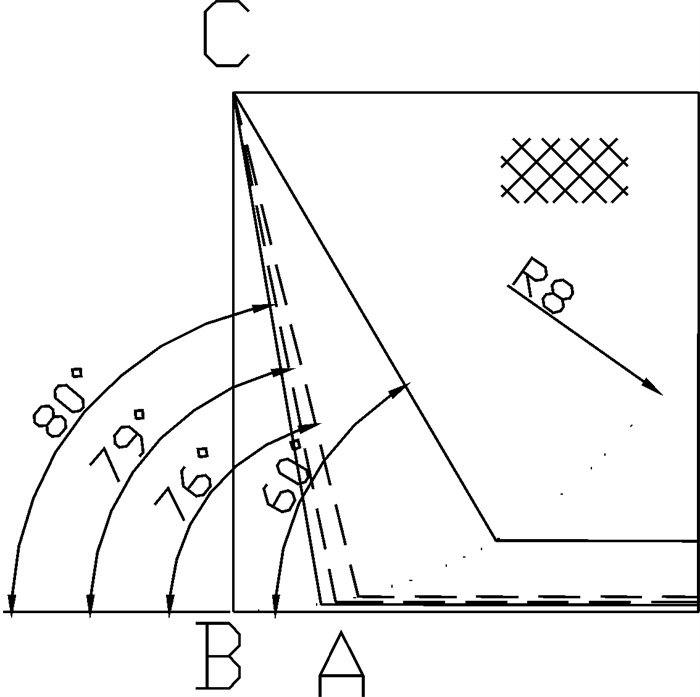
表 1 圆柱形囊网在不同流速下阻力近似值
Table 1 Approximate value of resistance to column cod-end at different velocity of flow
冲角a°
attack angle流速/m·s-1 velocity of flow 0.25 0.35 0.45 0.55 0.65 0.75 0.85 90 32 175 63 063 104 247 155 726 217 502 289 573 371 942 80 28 644 56 143 92 808 138 639 193 637 257 800 331 130 70 25 114 49 224 81 370 121 552 169 771 226 026 290 319 60 21 584 42 304 64 131 104 465 145 906 194 253 249 507 50 18 053 35 384 58 493 87 378 122 040 162 479 208 696 40 14 523 28 465 47 054 70 791 98 175 130 706 167 885 30 10 992 21 545 35 616 53 204 74 309 98 932 127 073 表 2 圆台形囊网锥度为8°~52°时在不同流速下阻力近似值
Table 2 Approximate value of resistance to truncated cone cod-end at cone angle of 8°~52°
N 冲角a°
attack angle1/2锥度
1/2 cone angle流速/m·s-1
velocity of flowR/r(m) 0.25 0.35 0.45 0.55 0.65 0.75 0.85 86 4 28 739 56 329 93 115 139 098 194 277 258 653 332 225 7.162/6.662 83 7 25 885 50 735 83 869 125 285 174 985 232 969 299 236 7.162/6.162 79 11 22 964 45 009 74 403 111 145 155 235 206 674 265 461 7.162/5.662 76 14 20 558 40 293 66 608 99 500 138 971 185 021 237 649 7.162/5.162 72 18 18 106 35 488 58 664 87 633 122 397 162 955 209 306 7.162/4.662 68 22 15 878 31 121 51 445 76 849 107 335 142 902 183 549 7.162/4.162 64 26 13 863 27 171 44 916 67 096 93 713 124 765 160 254 7.162/3.662 -
[1] 黄锡昌. 捕捞学[M]. 重庆: 重庆出版社, 2001.69-77. [2] 弗里德曼АЛ. 渔具理论与设计. 候恩淮, 高清廉译[M]. 北京: 海洋出版社, 1988.54. [3] 郭根喜, 陶启友. 深水网箱圆台形囊网的设计与制作[J]. 南方水产, 2005, 1(1): 47-53. doi: 10.3969/j.issn.2095-0780.2005.01.008 [4] 黄锡昌, 虞聪达, 苗振清. 中国远洋捕捞手册[M]. 上海: 上海科学技术文献出版社, 2003. 356. [5] Hjerpbakk Svein-Erik. Mooring study documentation, site at Mirs Bay, Shenzhen, China[R]. Norway: Helgeland Plast, 1999.
[6] Norway: Helgeland Plast AS. Polarcirkel-user manual[Z]. 1999.25-26.
-
期刊类型引用(8)
1. 唐元龙,谢迎春,袁昊训,李相坤. 聚乙烯网衣破损因素下的水动力特性与流场模拟. 渔业现代化. 2024(06): 20-30 .  百度学术
百度学术
2. 黄小华,刘海阳,胡昱,陶启友,王绍敏,袁太平. 深水养殖网箱浮架变形模拟及结构改进设计. 农业工程学报. 2018(15): 44-49 .  百度学术
百度学术
3. 黄小华,刘海阳,胡昱,陶启友,王绍敏,袁太平. HDPE圆形网箱单点系泊与多点系泊受力特性模拟分析比较. 浙江海洋大学学报(自然科学版). 2018(02): 140-146 .  百度学术
百度学术
4. 陈天华,潘昀,冯德军,孟昂,桂福坤. 固定方式对水流作用下桩柱式围网网片力学特性的影响. 水产学报. 2018(03): 452-460 .  百度学术
百度学术
5. 桂福坤,陈天华,赵云鹏,董国海. 固定方式对桩柱式围网网片波浪力学特性影响研究. 大连理工大学学报. 2017(03): 285-292 .  百度学术
百度学术
6. 李杰,晏磊,杨炳忠,张鹏. 罩网自由沉降过程的数值模拟研究. 南方水产科学. 2017(04): 105-114 .  本站查看
本站查看
7. 陈天华,孟昂,桂福坤. 波浪高度及方向对桩柱式围网养殖系统网片水力特性的影响. 农业工程学报. 2017(02): 245-251 .  百度学术
百度学术
8. 陈天华,潘昀,孟昂,桂福坤. 桩柱式围网单元网片在水流作用下的水动力特性研究. 水动力学研究与进展(A辑). 2017(04): 511-519 .  百度学术
百度学术
其他类型引用(6)




 下载:
下载:






 粤公网安备 44010502001741号
粤公网安备 44010502001741号
