Numerical simulation of the force and deformation of submerged plane nets in current
-
摘要:
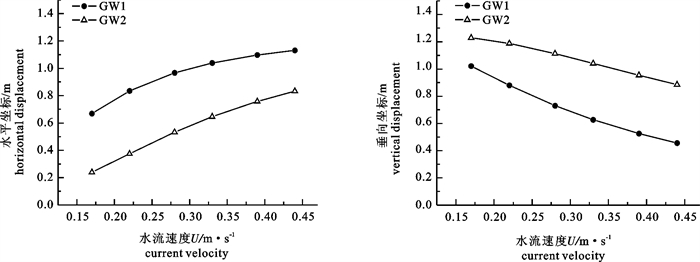
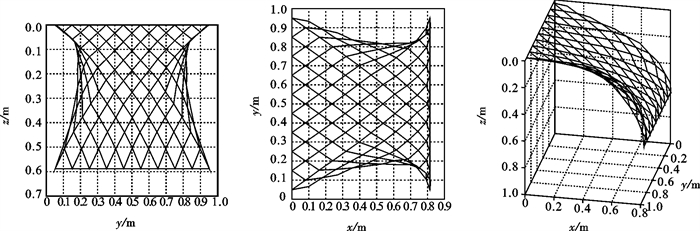
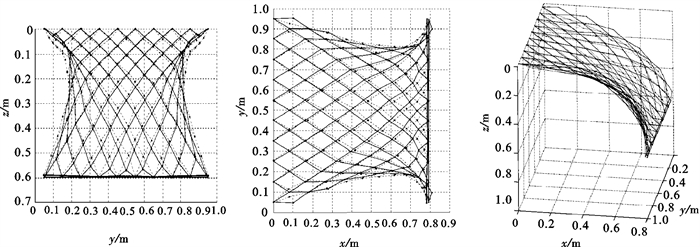
基于集中质量点法和牛顿第二定律，建立了网衣在水流作用下的受力和运动响应数学模型。采用计算机数值模拟方法，研究了水流作用下网衣的动态变形情况以及网衣受力平衡后的空间分布形状。在2种配重(GW1=4.12 N、GW2=16.38 N)和6种流速(U=0.17、0.22、0.28、0.33、0.39和0.44 m·s-1)条件下对网衣稳定后沿水流方向的总水流力、网衣底端的水平及垂直位移进行了数值计算。计算结果表明，配重及流速大小对网衣受力和变形特性具有较大的影响。随着水流速度的增大，网衣在水流作用下的运动变形加剧，且当配重增大时，网衣变形减小，网衣受力随流速的变化增幅明显加快。为了验证模型的正确性和有效性，文章还将数值模拟结果与前人的试验结果进行了比较，效果良好。
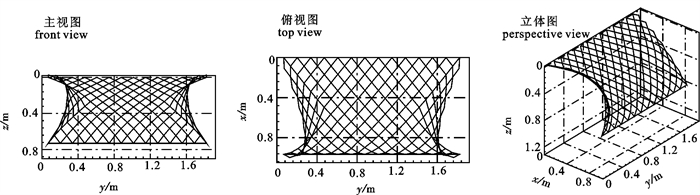
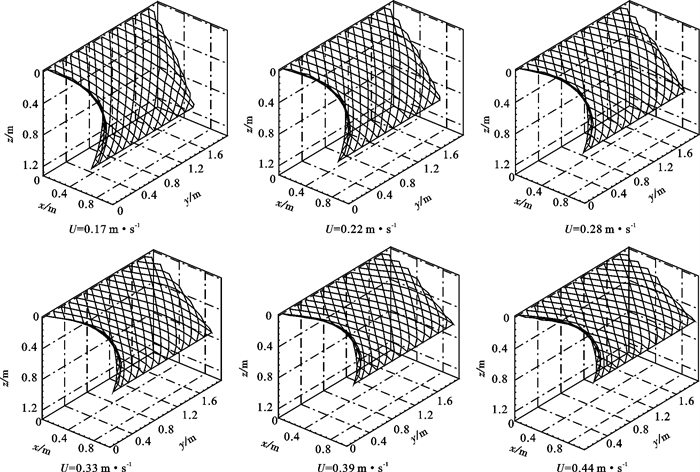
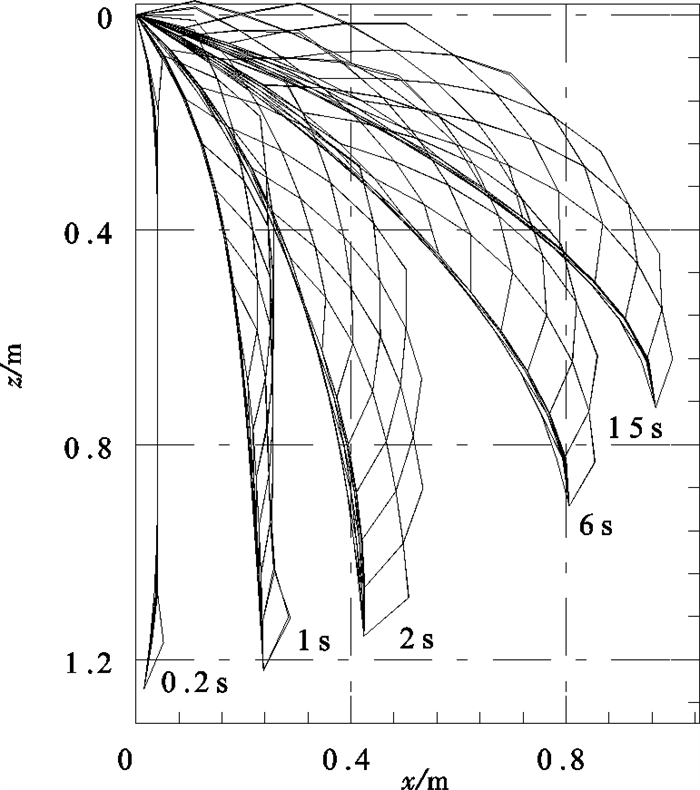
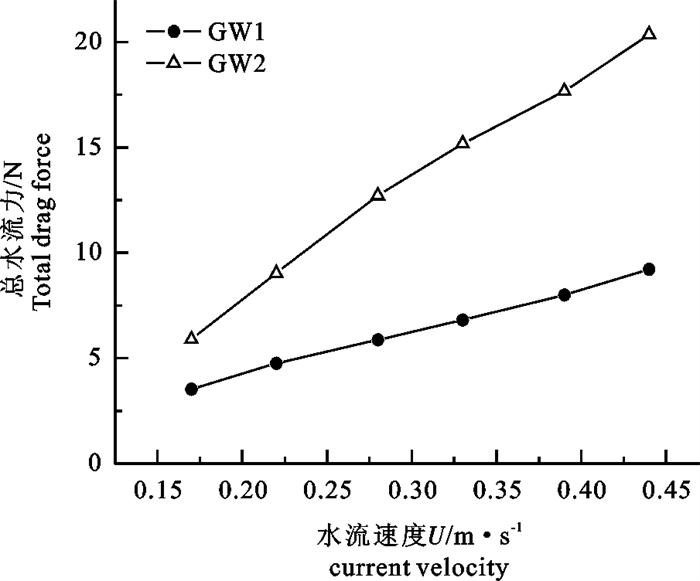
Abstract:Based on the lumped mass method and Newton′s second law, the numerical model of the force and movement response for fishing nets in current was set up, and then the dynamic deformation and the equilibrium configuration of the plane net in current along the positive direction of x-axis were studied by means of computer numerical simulation method. In this paper, under the conditions of two weight modes (GW1=4.12 N, GW2=16.38 N) and six current velocities (U=0.17, 0.22, 0.28, 0.33, 0.39 and 0.44 m·s-1), the total drag force in the forward flow and the horizontal and vertical displacements of the net bottom were calculated after the plane net getting equilibrium in current. The calculated results showed that the influences of weight system and current velocity on the characteristics of drag force and deformation of plane net are significant. With the increase of flow velocity, the motion deformation of the plane net in current was intensified obviously. Moreover, when the weight increased, the deformation of the net decreased accordingly, and the enhancement of the total drag force accelerated apparently with the flow velocity increasing. Simulated results consisted well with other investigator′s experimental data, which verified the accuracy and efficiency of the model.
-
Keywords:
- plane net /
- numerical simulation /
- current /
- lumped mass
-
巢湖地处长江中下游的安徽省中部，是我国著名的五大淡水湖之一，其地理坐标为东径117°16′54″~117°51′46″，北纬30°25′28″~31°43′28″，属长江左岸水系。全流域面积9 173 km2，涉及7县2市，地貌总体呈南北高，中间低，杭埠河、白石天河、兆河等主要河流呈向心状分布。湖区跨越2市、3县、1区，是沿湖地区工农业生产和群众生活用水的重要水源，是渔业生产的重要基地。农业部渔业生态环境监测中心将其作为编制2004年《中国渔业生态环境状况公报》的重点渔业水域，进行渔业生态环境监测。本文通过对调查、测定的结果进行综合分析，应用层次分析决策法对巢湖渔业生态环境进行评价。
1. 采样点选择及监测项目
通过对近年巢湖渔业调查分析，结合水域特点及入湖河流状况，确定了5月份巢湖鱼类生态环境监测点，见图 1。
监测项目：
(1) 生物环境监测：叶绿素a、浮游植物、浮游动物；
(2) 水质监测：水温、透明度、pH、溶解氧、电导率、总氮、总磷、非离子氨、高锰酸盐指数、铜、锌、铅、镉、汞、砷、石油类、挥发酚。
2. 层次分析
人们在决策过程中，往往会遇到无法定量化的因素，因而影响到决策的质量。美国著名运筹学家Saaty教授于20世纪70年代中期创立的层次分析法(Analytic Hierarchy Process，AHP)是一种能用来处理复杂的社会、政治、经济、科学技术等决策问题的新方法[1, 2]。渔业生态环境综合评价涉及到水域的生物环境和水质环境等多个因素，其环境的优劣类似一个多目标决策问题。它可在确定渔业最优环境这个总目标下，划分各分指标层和方案层，结合水环境综合评价的特点，建立评定渔业最优环境的层次结构模型。
2.1 建立递阶层次结构[3, 4, 9]
根据巢湖水域渔业环境的特点，结合生物监测、水质监测的结果，建立了巢湖水域渔业环境优劣评价系统的递阶层次结构。见图 2。
图 2中，最上层是目标层，各监测点渔业环境的优劣排序；第二层是指标层，该层因素为渔业环境两大类环境因子，因两大类环境因子优劣判断标准有差异，故这里把它们区分开，再细分成分指标层；最低层为方案层，即由不同指标数值组成的各监测点。
2.2 构造各层因素间的比较判断矩阵[5-8]
2.2.1 建立三标度比较矩阵
根据图 2的递阶层次结构，建立最上层至最低层逐层构造有关因素之间的两两比较判断矩阵。亦即对上一层某因素而言，在其下一层次上所有与它关联的因素中依次两两比较两者的重要性或有利关系，对指标而言按“重要”、“同等重要”和“不重要”，对方案而言按“有利”、“同样有利”和“不利”，分别用“2”、“1”和“0”三种数值标度定量表示。由此得出的三标度矩阵，它表示了各因素之间相对于上一层某因素的重要性或有利关系。如A因素与下一层次中的B1，B2，…，Bn有联系，其三标度矩阵的一般形式为：
A B1 B2 … Bn B1 b11 b12 … b1n B2 b21 b22 … b2n $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ Bn bn1 bn2 … bnn 或$ B=\left[\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 n} \\ b_{21} & b_{22} & \cdots & b_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ b_{n 1} & b_{n 2} & \cdots & b_{n n} \end{array}\right]=\left(b_{i j}\right)_{n \times n}$其中
$$ b_{i j}= \begin{cases}2 & \text { 在 } A \text { 因素下, } B_i \text { 比 } B_j \text { 重要或有利 } \\ 1 & \text { 在 } A \text { 因素下, } B_i \text { 与 } B_j \text { 同样重要或有利 } \\ 0 & \text { 在 } A \text { 因素下, } B_i \text { 没有 } B_j \text { 重要或有利 }\end{cases} $$ 且有bii=1，即在A因素下，Bi自身比较，重要性或有利关系相同。
按上述方法，巢湖宜渔指标，据专家定权法建立三标度比较矩阵分别为：
A1—B A1 B1 B2 B3 B4 B5 B6 B7 ri 基点base point B1 1 2 0 0 2 2 0 7 rmax=13→B3
rmin=1 →B2
dm(B3: B2)=7B2 0 1 0 0 0 0 0 1 B3 2 2 1 2 2 2 2 13 B4 2 2 0 1 2 2 2 11 B5 0 2 0 0 1 0 0 3 B6 0 2 0 0 2 1 0 5 B7 2 2 0 0 2 2 1 9 B1—C B1 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 2 2 1 6 rmax=9→C2
rmin=1 →C3
dm(C2: C3)=5C2 2 1 2 2 2 9 C3 0 0 1 1 0 1 C4 0 0 2 2 0 3 C5 1 0 2 2 1 6 B2—C B2 C1 C2 C3 C4 C5 ri 基点base point C1 1 2 2 0 0 5 rmax=9→C5
rmin=1→C3
dm(C5: C3)=3C2 0 1 2 0 0 3 C3 0 0 1 0 0 1 C4 2 2 2 1 0 7 C5 2 2 2 2 1 9 B3—C B3 C1 C2 C3 C4 C5 ri 基点base point C1 1 2 2 2 2 9 rmax=9→C1
rmin=1 →C4
dm(C1: C4)=5C2 0 1 0 2 0 3 C3 0 2 1 2 0 5 C4 0 0 0 1 0 1 C5 0 2 2 2 1 7 B4—C B4 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=9→C5
rmin=1→C1
dm(C5: C1)=3C2 2 1 2 2 0 7 C3 2 0 1 2 0 5 C4 2 0 0 1 0 3 C5 2 2 2 2 1 9 B5—C B5 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=9→C3
rmin=1→C1
dm(C3: C1)=7C2 2 1 0 2 2 7 C3 2 2 1 2 2 9 C4 2 0 0 1 2 5 C5 2 0 0 0 0 3 B6—C B6 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=9→C4
rmin=1→C1
dm(C4: C1)=3C2 2 1 0 0 2 5 C3 2 2 1 0 2 7 C4 2 2 2 1 2 9 C5 2 0 0 0 1 3 B7—C B7 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=7→C2、C4、C5
rmin=1→C1
dm(C2: C1)=3C2 2 1 2 1 1 7 C3 2 0 1 0 0 3 C4 2 1 2 1 1 7 C5 2 1 2 1 1 7 2.2.2 求出AHP间接判断矩阵
三标度比较矩阵并不能准确地反映各因素在某准则下的相对重要性程度，因此必须将其变换成具有层次分析法特点和性质的间接判断矩阵。首先，计算各因素的排序指数：
$$ r_i=\sum\limits_{j=1}^n b_{i j} \quad \mathrm{i}=1, 2, \cdots, n $$ 再找出最大排序指数rmax和最小排序指数rmin：
$$ \begin{aligned} & r_{\max }=\max _{1 \leq i \leq n}\left\{r_i\right\} \\ & r_{\min }=\min _{1 \leq i \leq n}\left\{r_i\right\} \end{aligned} $$ 以Bmax、Bmin分别表示与rmax、rmin对应的因素，则当选取Bmax、Bmin作为基点比较因素，并按9标度数值给出这个基点的相对重要程度dm后，利用下面的变换式可求得反映各因素间相对重要性程度的AHP间接判断矩阵：
$$ D=\left[\begin{array}{cccc} d_{11} & d_{12} & \cdots & d_{1 n} \\ d_{21} & d_{22} & \cdots & d_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ d_{n 1} & d_{n 2} & \cdots & d_m \end{array}\right]=\left(d_{i j}\right)_{n \times n} $$ $$ d_{i j}= \begin{cases}\frac{r_i-r_j}{r_{\max }-r_{\min }}\left(d_m-1\right)+1 & r_i-r_j \geq 0 \\ {\left[\frac{r_j-r_i}{r_{\max }-r_{\min }}\left(d_m-1\right)+1\right]^{-1}} & r_i-r_j<0\end{cases} $$ 采用ri计算式算得ri各值，列在每一比较矩阵的倒数第二列，rmax、rmin以及它们对应的Bmax、Bmin的基点相对重要性程度dm，列在每一比较矩阵的最后一列。然后利用dij计算式算得各个AHP间接判断矩阵如下：
A1—B A1 B1 B2 B3 B4 B5 B6 B7 权向量
weight vector一致性检验
consistency checkB1 1 4 1/4 1/3 3 2 1/2 0.1040 λmax=7.1952
C.I.=0.0325
R.I.=1.32
C.R.=0.0246B2 1/4 1 1/7 1/6 1/2 1/3 1/5 0.0308 B3 4 7 1 2 6 5 3 0.3517 B4 3 6 1/2 1 5 4 2 0.2412 B5 1/3 2 1/6 1/5 1 1/2 1/4 0.0449 B6 1/2 3 1/5 1/4 2 1 1/3 0.0678 B7 2 5 1/3 1/2 4 3 1 0.1596 B1—C B1 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 2/5 7/2 5/2 1 0.2078 λmax=5.0602
C.I.=0.0150
R.I.=1.12
C.R.=0.0134C2 5/2 1 5 4 5/2 0.4250 C3 2/7 1/5 1 1/2 2/7 0.0618 C4 2/5 1/4 2 1 2/5 0.0976 C5 1 2/5 2/7 5/2 1 0.2078 B2—C B2 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 3/2 2 2/3 1/2 0.1821 λmax=5.0596
C.I.=0.0149
R.I.=1.12
C.R.=0.0133C2 2/3 1 2/3 1/2 2/5 0.1122 C3 1/2 3/2 1 2/5 1/3 0.1149 C4 3/2 2 5/2 1 2/3 0.2513 C5 2 5/2 3 3/2 1 0.3395 B3—C B3 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 4 3 5 2 0.4174 λmax=5.0682
C.I.=0.0170
R.I.=1.12
C.R.=0.0152C2 1/4 1 1/2 2 1/3 0.0975 C3 1/3 2 1 3 1/2 0.1602 C4 1/5 1/2 1/3 1 1/4 0.0615 C5 1/2 3 2 4 1 0.2634 B4—C B4 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 2/5 1/2 2/3 1/3 0.0975 λmax=5.0143
C.I.=0.0036
R.I.=1.12
C.R.=0.0032C2 5/2 1 3/2 2 2/3 0.2506 C3 2 2/3 1 3/2 1/2 0.1816 C4 3/2 1/2 2/3 1 2/5 0.1317 C5 3 3/2 2 5/2 1 0.3386 B5—C B5 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 2/11 1/7 1/4 2/5 0.0435 λmax=5.1464
C.I.=0.0366
R.I.=1.12
C.R.=0.0327C2 11/2 1 2/5 5/2 4 0.2656 C3 7 5/2 1 4 11/2 0.4707 C4 4 2/5 1/4 1 5/2 0.1431 C5 5/2 1/4 2/11 2/5 1 0.0771 B6—C B6 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 1/2 2/5 1/3 2/3 0.0974 λmax=5.0143
C.I.=0.0036
R.I.=1.12
C.R.=0.0032C2 2 1 2/3 1/2 3/2 0.1817 C3 5/2 3/2 1 2/3 2 0.2506 C4 3 2 3/2 1 5/2 0.3386 C5 3/2 2/3 1/2 2/5 1 0.1317 B7—C B7 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 1/3 3/5 1/3 1/3 0.0840 λmax=5.0080
C.I.=0.0020
R.I.=1.12
C.R.=0.0018C2 3 1 7/3 1 1 0.2654 C3 5/3 2/7 1 3/7 3/7 0.1198 C4 3 1 7/3 1 1 0.2654 C5 3 1 7/3 1 1 0.2654 2.3 由AHP间接判断矩阵计算权重[4, 8]
求解出间接判断矩阵的最大特征值λmax、C.I.及对应的特征量，将其归一化后即为某一层的有关因素相对于上一层相关因素的权重值。判断矩阵的一致性可用λmax、C.I.、R.I.和C.R.指标来检验，C.I.=(λmax-n)/(n-1)，R.I.按表 1确定，随机一致性比值C.R.=C.I./R.I.，当C. I.＜0.1时，则认为判断矩阵符合一致性要求。
表 1 平均一致性指标Table 1. The average consistency indicatorn 1 2 3 4 5 6 7 8 9 R.I. 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 用方根法求出各个间接判断矩阵的权向量和一致性检验指标，分别列在每个间接判断矩阵的后两列。然后求出5个监测点C1、C2、C3、C4和C5对于宜渔指标A1而言，相对优劣排序及一致性检验，见表 2。
表 2 A1—B—C层次总排序Table 2. The general arrangement for layers A1—B—CA1 B1
0.1040B2
0.0308B3
0.3517B4
0.2412B5
0.0449B6
0.0678B7
0.1596层次总排序
layers sequencing一致性检验
consistency checkC1 0.2078 0.1821 0.4174 0.0975 0.0435 0.0974 0.0840 0.2195 C.I.=0.0111
R.I.=1.12
C.R.=0.0099C2 0.4250 0.1122 0.0975 0.2506 0.2656 0.1817 0.2654 0.2091 C3 0.0618 0.1149 0.1602 0.1816 0.4707 0.2506 0.1198 0.1674 C4 0.0976 0.2513 0.0615 0.1317 0.1431 0.3386 0.2654 0.1430 C5 0.2078 0.3395 0.2634 0.3386 0.0771 0.1317 0.2654 0.2610 由表 2可见，相对于宜渔指标A1这个目标而言，5个监测点C1、C2、C3、C4和C5相对优劣排序为：C5＞C1＞C2＞C3＞C4。因此，E点宜渔指标最好。
按照上面方法，分析巢湖水质指标，计算出A2—B—C层次总排序，见表 3。
表 3 A2—B—C层次总排序Table 3. The general arrangement for layers A2—B—CA2 B1
0.5690B5
0.0523B6
0.2741B8
0.0523B9
0.0523层次总排序
layers sequncing一致性检验
consistency checkC1 0.1253 0.0435 0.0615 0.0615 0.0615 0.0969 C.I.=0.0169 R.I.=1.12 C.R.=0.0151 C2 0.0613 0.1431 0.1602 0.0975 0.2634 0.1051 C3 0.4213 0.0771 0.2634 0.1602 0.4174 0.3462 C4 0.2668 0.2656 0.4174 0.4174 0.1602 0.3103 C5 0.1253 0.4707 0.0975 0.2634 0.0975 0.1415 由表 3可见，相对于水质指标A2这个目标而言，5个监测点C1、C2、C3、C4和C5相对优劣排序为：C3＞C4＞C5＞C2＞C1。因此，C点水质指标最好。
最后，求出宜渔指标A1和水质指标A2对于巢湖渔业环境优劣总目标层M的层次的排序及一致性检验，见表 4。
表 4 M—A—B—C层次总排序Table 4. The general arrangement for layers A3—B—CM A1
0.35A2
0.65层次总排序
layers sequencing一致性检验
consistency checkC1 0.2195 0.0969 0.1398 C.I.=0.01149
R.I.=1.12
C.R.=0.0133C2 0.2091 0.1051 0.1416 C3 0.1674 0.3462 0.2836 C4 0.1430 0.3103 0.2517 C5 0.2610 0.1415 0.1833 由表 4可见，相对于巢湖渔业环境优劣总目标层M而言，通过综合宜渔指标A1和水质指标A2等多因素的评判，最后得出5个监测点相对优劣总排序为：C3＞C4＞C5＞C2＞C1。因此，巢湖渔业环境C3(即监测点C)点指标最好。
3. 讨论
巢湖渔业环境5个监测点，C点渔业环境相对最好。C点水体单元位于巢湖东湖湖心，外源性污染影响较小，水域环境相对稳定，该水域同其它水域之间存在着明显的差异。从C点的生物环境来看，该点的蓝藻数量亦最低；蓝藻数量低，其对其它浮游生物的抑制作用就小，该点的生物多样性就会增加，区域内的小生境就会较其它水域好。从叶绿素a监测的结果可以看出C点的含量最低(0.094 μg · L-1)，低于一般湖泊富营养化标准值(0.1 μg · L-1)。从C点的水质环境来看，监测的17个因子中，有14个优于渔业水质标准；有3个超标，分别是总氮、总磷和石油类，该域水质总体尚可。
巢湖A点渔业环境相对最差。从A点的生物环境来看，该点的浮游生物数量和生物量都最高，其蓝藻数量也是全湖中最高的。从A点的水质环境来看，A点在巢湖的西湖区，有着众多的入湖河口，如南淝河、派河、丰乐河、杭埠河等，其中南淝河、派河向巢湖排入大量的城市污水，也是导致巢湖富营养化的主要原因之一，在水质监测结果中，A点的水质超标因子数是最多的。
监测点D、E同处巢湖的东部，巢湖地处亚热带江淮平原，夏季主导风向为东南风，处上风口；D点采样点在东口门，距柘皋河口与裕溪河口较近，E点采样点距烔炀河口较近。B点处于巢湖南部，距马尾河口不远，同D点、E点水体单元在地理、气象、水文、生物环境等方面具有较显著的相似性，仅区别于入湖径流不同。层次分析的结果说明，D点渔业环境优于E点，E点优于B点。
因此，从AHP的分析结果可以看出，巢湖水域的渔业生态环境，东湖湖心最好，东湖近岸水域次之，西湖水域最差。
-
![]()
图 3 水质点与构件相对速度示意图
Figure 3. Relative velocity of the water particle and the net segment
![]()
图 4 网衣集中质量点计算示意图
Figure 4. Schematic diagram of the lumped mass point for the calculations for mesh model
![]()
图 5 水流作用下网衣稳定后的空间形状图(配重GW1，U=0.28 m·s-1)
Figure 5. The equilibrium configuration of the plane net in current with weight mode GW1, U=0.28 m·s-1
![]()
图 6 配重GW1，不同流速时的网衣平衡形状图
Figure 6. The equilibrium configuration of the plane net for different flow velocities with weight mode GW1
![]()
图 7 不同时刻的网衣动态形状侧视图(配重GW1，U=0.28 m·s-1)
Figure 7. The configuration of the plane net with weight mode GW1, U=0.28 m·s-1, t=0.2, 1.0, 2.0, 6.0, 15 s
![]()
图 8 配重GW1和GW2 2种方案下水流力随流速的变化图
Figure 8. Relationship between the horizontal force of the net and current velocity in weight modes GW1 and GW2
![]()
图 9 配重GW1和GW2 2种方案下网衣底端坐标随流速的变化图
Figure 9. Relationship between the displacement of the net bottom and current velocity in weight modes GW1 and GW2
![]()
图 10 流速U=0.4 m·s-1时的网衣变形模拟结果
Figure 10. Simulation results of the deformation of the net when U=0.4 m·s-1
-
[1] TSUKROV I, EROSHKIN O, FREDRIKSSON D, et al. Finite element modeling of net panels using a consistent net element[J]. Ocean Eng, 2003, 30(2): 251-270. doi: 10.1016/S0029-8018(02)00021-5
[2] BESSONNEAU J S, MARICHAL D. Study of the dynamics of submerged supple nets (applications to trawls)[J]. Ocean Eng, 1998, 25(7): 563-583. doi: 10.1016/S0029-8018(97)00035-8
[3] SUZUKI K, TAKAGI T, SHIMIZU T, et al. Validity and visualization of a numerical model used to determine dynamic configurations of fishing nets[J]. Fish Sci, 2003, 69(4): 695-705. doi: 10.1046/j.1444-2906.2003.00676.x
[4] TAKAGI T, SUZUKI K, HIRAISHI T. Development of the numerical simulation method of dynamic fishing net shape[J]. Nippon Suisan Gakkaishi, 2002, 68(3): 320-326. doi: 10.2331/suisan.68.320
[5] TAKAGI T, SUZUKI K, HIRAISHI T. Modeling of net for calculation method of dynamic fishing net shape[J]. Fish Sci, 2002, 68(Suppl. ): 1 857-1 860. https://www.jstage.jst.go.jp/article/fishsci1994/68/sup2/68_sup2_1857/_article
[6] LADER P F, ENERHAUG B, FREDHEIM A, et al. Modelling of 3D net structures exposed to waves and current[C]. Proceedings of the 3rd International Conference on Hydroelasticity in Marine Technology. Trondheim, Norway: SINTEF Fisheries and Aquaculture 2003: 19-26. http://www.researchgate.net/publication/237322515_Modelling_of_3D_Net_Structures_Exposed_to_Waves_and_Current
[7] LADER P F, FREDHEIM A. Dynamic properties of a flexible net sheet in waves and current-A numerical approach[J]. Aquac Eng, 2006, 35(3): 228-238. doi: 10.1016/j.aquaeng.2006.02.002
[8] 詹杰民, 胡由展, 赵陶, 等. 渔网水动力试验研究及分析[J]. 海洋工程, 2002, 20(2): 49-54. doi: 10.3969/j.issn.1005-9865.2002.02.009 [9] ZHAN J M, JIA X P, LI Y S, et al. Analytical and experimental investigation of drag on nets of fish cages[J]. Aquac Eng, 2006, 35(1): 91-101. doi: 10.1016/j.aquaeng.2005.08.013
[10] WAN R, HU F X, TOKAI T. A static analysis of the tension and configuration of submerged plane nets[J]. Fish Sci, 2002, 68(4): 815-823. doi: 10.1046/j.1444-2906.2002.00497.x
[11] WAN R, HUANG W Q, SONG X F, et al. Statics of a gillnet placed in a uniform current[J]. Ocean Eng, 2004, 31(14/15): 1 725-1 740. https://www.sciencedirect.com/science/article/pii/S0029801804000678
[12] 万荣, 宋协法, 唐衍力. 养殖网箱耐流特性的计算机数值模拟[C]. 第一届海洋生物高技术论坛论文集. 北京: 海洋出版社, 2001: 361-365. https://d.wanfangdata.com.cn/conference/6736063 [13] 李玉成, 赵云鹏, 董国海, 等. 波浪与水流对重力式网箱作用的数值模拟[C]. 第二十届全国水动力研讨会会议文集, 北京: 海洋出版社, 2007: 687-694. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-SLDX200708001095.htm [14] 李玉成, 桂福坤, 宋芳, 等. 漂浮状态下重力式与碟形网箱的锚绳受力特性比较[J]. 水产学报, 2005, 29(4): 570-573. doi: 10.3321/j.issn:1000-0615.2005.04.024 [15] ZHAO Y P, LI Y C, GUI F K, et al. Numerical simulation of the effects of weight system on the hydrodynamic behaviour of 3D net of gravity cage in current[J]. J Hydrodynamics Ser B, 2007, 19(4): 442-452. doi: 10.1016/S1001-6058(07)60138-3
[16] 唐宏结. 网箱容积变形改善研究[D]. 台北: 国立中山大学, 2002. [17] 苏炜, 詹杰民. 等效网面法在模拟网的水动力特性中的应用[J]. 水动力学研究与进展A辑, 2007, 22(3): 267-272. doi: 10.3969/j.issn.1000-4874.2007.03.001 [18] GERHARD K. Fibre ropes for fishing gear[M]. FAO Fishing Manuals, 1983: 81-124. http://agris.fao.org/agris-search/search.do?recordID=XF19840046526
[19] 郑咸义. 计算方法[M]. 广州: 华南理工大学出版社, 2003: 213-232. -
期刊类型引用(1)
1. 杨光昕，张骏宇，夏薇，汪珑珑，沈晓盛，樊成奇，田晓清，孔聪. 垂钓饵料中地西泮在鲫鱼体内代谢及组织分布研究. 食品安全质量检测学报. 2025(01): 119-126 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 1
粤公网安备 44010502001741号
