Variation and accumulation characteristics of diazepam in simulated culture environment
-
摘要:
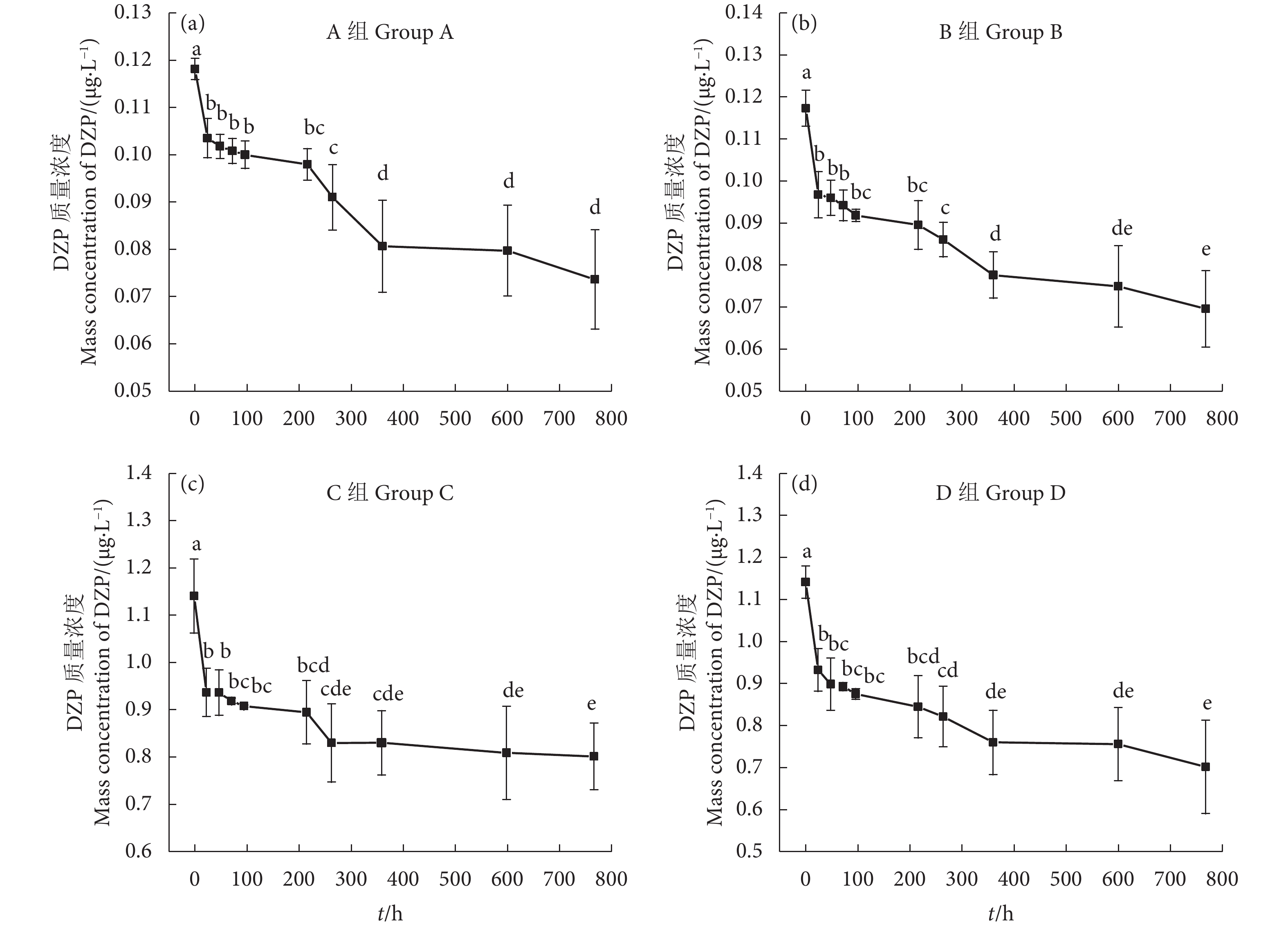
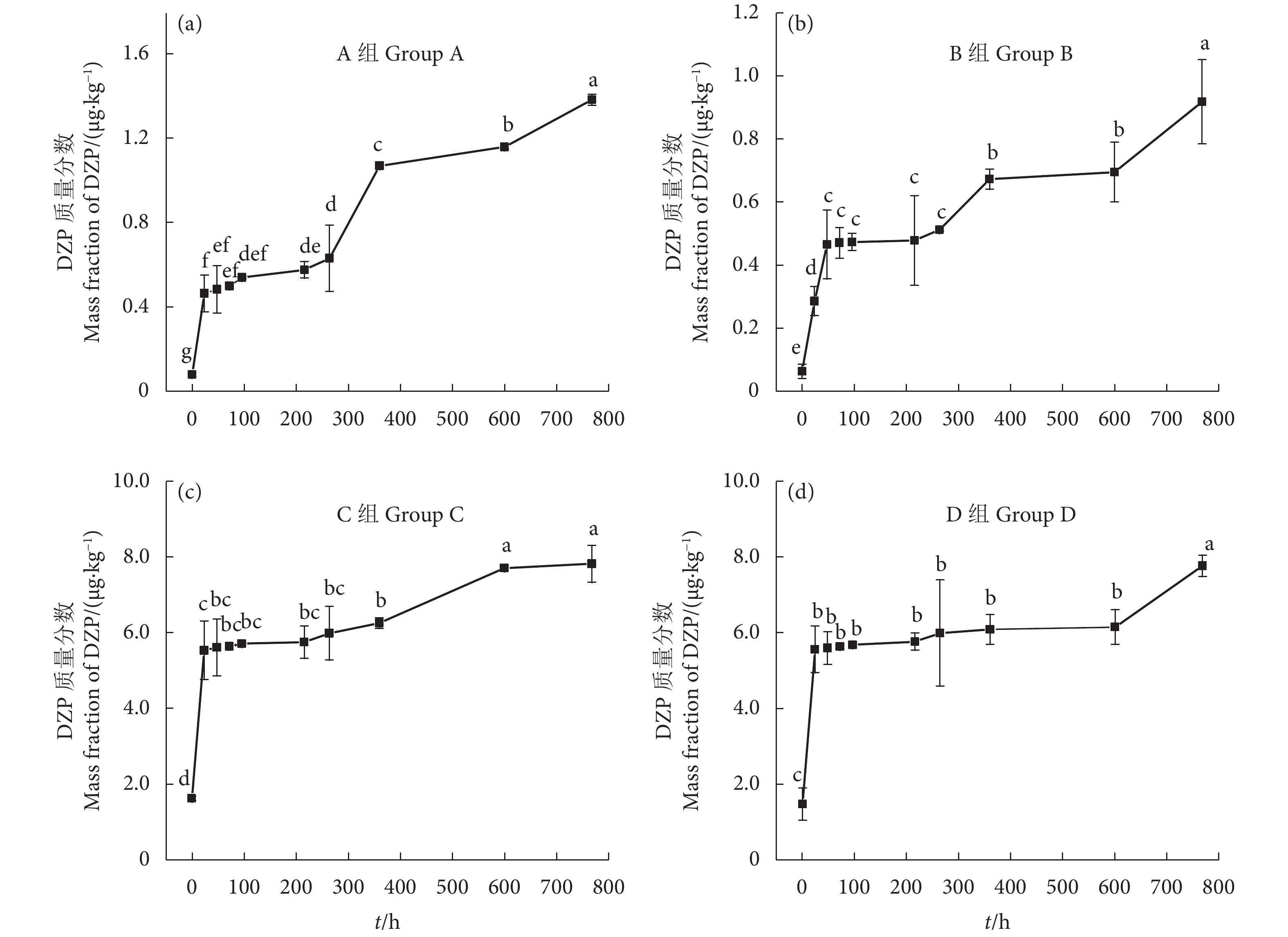
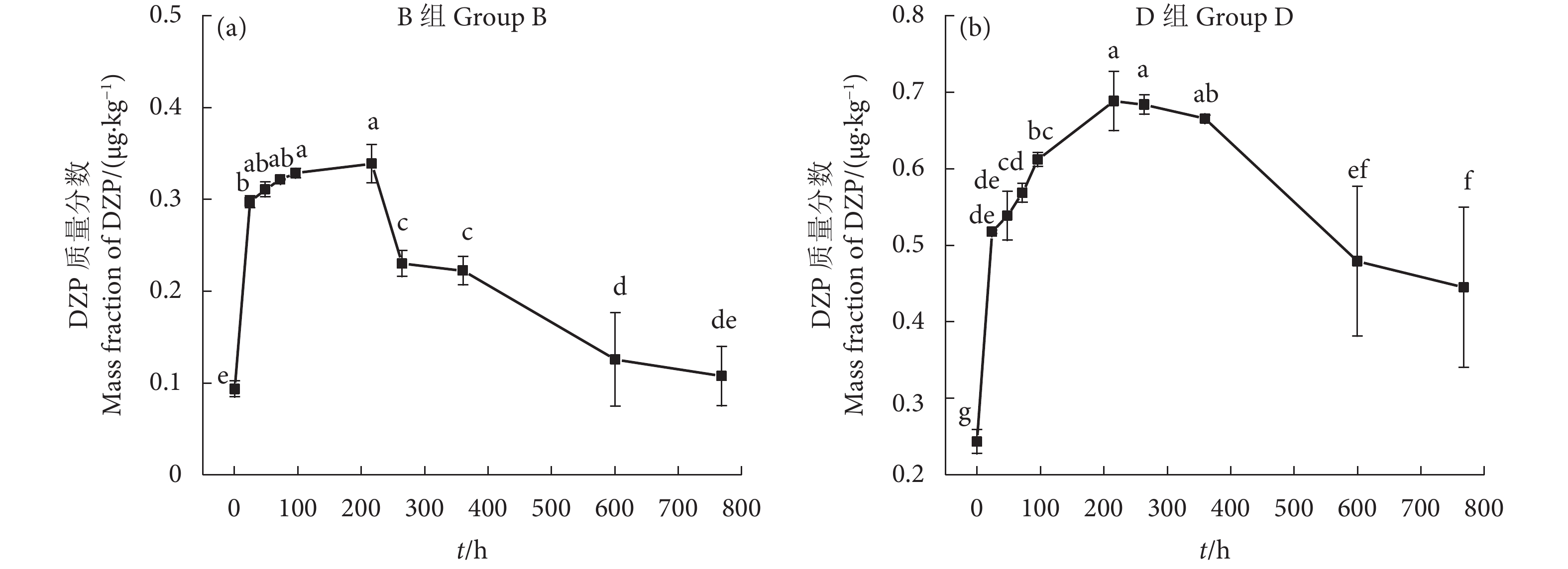
为探究地西泮 (Diazepam, DZP) 在模拟养殖环境中的降解特点及累积特征，设置2个浓度胁迫组 (A、C组)，并在2个浓度下添加蜈蚣草 (Pteris vittata) 作对照组 (B、D组)，共4个试验组；分析水体、底泥和蜈蚣草中DZP浓度随时间的变化特点，探讨蜈蚣草和底泥对水体中DZP的累积特征。结果表明，给药后4组水体中DZP的初始质量浓度分别为A：(0.118±0.002) μg·L−1、B：(0.117±0.004) μg·L−1、C：(1.141±0.078) μg·L−1和D：(1.142±0.039) μg·L−1，给药后第768小时水体中DZP质量浓度下降了29.71%~40.17%；DZP降解半衰期介于65.29~139.11 d。4组底泥中DZP质量分数随时间变化逐渐上升，给药768 h后4组底泥中DZP质量分数分别达到初始质量分数的17.99倍(1.384 μg·kg−1)、14.81倍(0.918 μg·kg−1)、4.77倍 (7.848 μg·kg−1)和5.30倍 (7.763 μg·kg−1)，富集系数介于9.79~18.80；B、D组蜈蚣草中DZP浓度峰值出现在给药后第216小时。蜈蚣草和底泥对水体中的DZP具有一定的吸附和富集作用，可明显缩短高浓度DZP在水中降解的半衰期，在低浓度DZP水体中添加蜈蚣草可抑制底泥对DZP的富集。
Abstract:In order to explore the degradation and accumulation characteristics of diazepam (DZP) in simulated culture environment, we set up four experimental groups including two different concentration stress groups (Group A and Group C) and two control groups (Group B and Group D) with addition of Pteris vittata to analyze the changes of DZP content in water, sediment and P. vittata with time, and to investigate the accumulation characteristics of DZP in water by P. vittata and sediment. The results show that the initial DZP mass concentrations in Group A, Group B, Group C and Group D were (0.118±0.002) μg·L−1, (0.117±0.004) μg·L−1, (1.141±0.078) μg·L−1 and (1.142±0.039) μg·L−1, respectively. The DZP concentration had decreased by 29.71%–40.17% after 768 h, and the degradation half-life period of DZP ranged from 65.29 d to 139.11 d. The DZP concentration in the sediment in the four groups increased gradually with time, reaching 17.99 times (1.384 μg·kg−1, dry mass), 14.81 times (0.918 μg·kg−1, dry mass), 4.77 times (7.848 μg·kg−1, dry mass) and 5.30 times (7.763 μg·kg−1, dry mass) of the initial concentration after 768 h of administration, respectively. The enrichment coefficients were 9.79–18.80. The peak concentration of DZP in Group B and Group D appeared after 216 h after administration. The adsorption and enrichment of DZP in water by P. vittata and the sediment can obviously shorten the degradation half-life period of high concentration DZP in water, and addition of P. vittata to low concentration DZP can inhibit the enrichment of DZP in sediment.
-
巢湖地处长江中下游的安徽省中部，是我国著名的五大淡水湖之一，其地理坐标为东径117°16′54″~117°51′46″，北纬30°25′28″~31°43′28″，属长江左岸水系。全流域面积9 173 km2，涉及7县2市，地貌总体呈南北高，中间低，杭埠河、白石天河、兆河等主要河流呈向心状分布。湖区跨越2市、3县、1区，是沿湖地区工农业生产和群众生活用水的重要水源，是渔业生产的重要基地。农业部渔业生态环境监测中心将其作为编制2004年《中国渔业生态环境状况公报》的重点渔业水域，进行渔业生态环境监测。本文通过对调查、测定的结果进行综合分析，应用层次分析决策法对巢湖渔业生态环境进行评价。
1. 采样点选择及监测项目
通过对近年巢湖渔业调查分析，结合水域特点及入湖河流状况，确定了5月份巢湖鱼类生态环境监测点，见图 1。
监测项目：
(1) 生物环境监测：叶绿素a、浮游植物、浮游动物；
(2) 水质监测：水温、透明度、pH、溶解氧、电导率、总氮、总磷、非离子氨、高锰酸盐指数、铜、锌、铅、镉、汞、砷、石油类、挥发酚。
2. 层次分析
人们在决策过程中，往往会遇到无法定量化的因素，因而影响到决策的质量。美国著名运筹学家Saaty教授于20世纪70年代中期创立的层次分析法(Analytic Hierarchy Process，AHP)是一种能用来处理复杂的社会、政治、经济、科学技术等决策问题的新方法[1, 2]。渔业生态环境综合评价涉及到水域的生物环境和水质环境等多个因素，其环境的优劣类似一个多目标决策问题。它可在确定渔业最优环境这个总目标下，划分各分指标层和方案层，结合水环境综合评价的特点，建立评定渔业最优环境的层次结构模型。
2.1 建立递阶层次结构[3, 4, 9]
根据巢湖水域渔业环境的特点，结合生物监测、水质监测的结果，建立了巢湖水域渔业环境优劣评价系统的递阶层次结构。见图 2。
图 2中，最上层是目标层，各监测点渔业环境的优劣排序；第二层是指标层，该层因素为渔业环境两大类环境因子，因两大类环境因子优劣判断标准有差异，故这里把它们区分开，再细分成分指标层；最低层为方案层，即由不同指标数值组成的各监测点。
2.2 构造各层因素间的比较判断矩阵[5-8]
2.2.1 建立三标度比较矩阵
根据图 2的递阶层次结构，建立最上层至最低层逐层构造有关因素之间的两两比较判断矩阵。亦即对上一层某因素而言，在其下一层次上所有与它关联的因素中依次两两比较两者的重要性或有利关系，对指标而言按“重要”、“同等重要”和“不重要”，对方案而言按“有利”、“同样有利”和“不利”，分别用“2”、“1”和“0”三种数值标度定量表示。由此得出的三标度矩阵，它表示了各因素之间相对于上一层某因素的重要性或有利关系。如A因素与下一层次中的B1，B2，…，Bn有联系，其三标度矩阵的一般形式为：
A B1 B2 … Bn B1 b11 b12 … b1n B2 b21 b22 … b2n $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ Bn bn1 bn2 … bnn 或$ B=\left[\begin{array}{cccc} b_{11} & b_{12} & \cdots & b_{1 n} \\ b_{21} & b_{22} & \cdots & b_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ b_{n 1} & b_{n 2} & \cdots & b_{n n} \end{array}\right]=\left(b_{i j}\right)_{n \times n}$其中
$$ b_{i j}= \begin{cases}2 & \text { 在 } A \text { 因素下, } B_i \text { 比 } B_j \text { 重要或有利 } \\ 1 & \text { 在 } A \text { 因素下, } B_i \text { 与 } B_j \text { 同样重要或有利 } \\ 0 & \text { 在 } A \text { 因素下, } B_i \text { 没有 } B_j \text { 重要或有利 }\end{cases} $$ 且有bii=1，即在A因素下，Bi自身比较，重要性或有利关系相同。
按上述方法，巢湖宜渔指标，据专家定权法建立三标度比较矩阵分别为：
A1—B A1 B1 B2 B3 B4 B5 B6 B7 ri 基点base point B1 1 2 0 0 2 2 0 7 rmax=13→B3
rmin=1 →B2
dm(B3: B2)=7B2 0 1 0 0 0 0 0 1 B3 2 2 1 2 2 2 2 13 B4 2 2 0 1 2 2 2 11 B5 0 2 0 0 1 0 0 3 B6 0 2 0 0 2 1 0 5 B7 2 2 0 0 2 2 1 9 B1—C B1 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 2 2 1 6 rmax=9→C2
rmin=1 →C3
dm(C2: C3)=5C2 2 1 2 2 2 9 C3 0 0 1 1 0 1 C4 0 0 2 2 0 3 C5 1 0 2 2 1 6 B2—C B2 C1 C2 C3 C4 C5 ri 基点base point C1 1 2 2 0 0 5 rmax=9→C5
rmin=1→C3
dm(C5: C3)=3C2 0 1 2 0 0 3 C3 0 0 1 0 0 1 C4 2 2 2 1 0 7 C5 2 2 2 2 1 9 B3—C B3 C1 C2 C3 C4 C5 ri 基点base point C1 1 2 2 2 2 9 rmax=9→C1
rmin=1 →C4
dm(C1: C4)=5C2 0 1 0 2 0 3 C3 0 2 1 2 0 5 C4 0 0 0 1 0 1 C5 0 2 2 2 1 7 B4—C B4 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=9→C5
rmin=1→C1
dm(C5: C1)=3C2 2 1 2 2 0 7 C3 2 0 1 2 0 5 C4 2 0 0 1 0 3 C5 2 2 2 2 1 9 B5—C B5 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=9→C3
rmin=1→C1
dm(C3: C1)=7C2 2 1 0 2 2 7 C3 2 2 1 2 2 9 C4 2 0 0 1 2 5 C5 2 0 0 0 0 3 B6—C B6 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=9→C4
rmin=1→C1
dm(C4: C1)=3C2 2 1 0 0 2 5 C3 2 2 1 0 2 7 C4 2 2 2 1 2 9 C5 2 0 0 0 1 3 B7—C B7 C1 C2 C3 C4 C5 ri 基点base point C1 1 0 0 0 0 1 rmax=7→C2、C4、C5
rmin=1→C1
dm(C2: C1)=3C2 2 1 2 1 1 7 C3 2 0 1 0 0 3 C4 2 1 2 1 1 7 C5 2 1 2 1 1 7 2.2.2 求出AHP间接判断矩阵
三标度比较矩阵并不能准确地反映各因素在某准则下的相对重要性程度，因此必须将其变换成具有层次分析法特点和性质的间接判断矩阵。首先，计算各因素的排序指数：
$$ r_i=\sum\limits_{j=1}^n b_{i j} \quad \mathrm{i}=1, 2, \cdots, n $$ 再找出最大排序指数rmax和最小排序指数rmin：
$$ \begin{aligned} & r_{\max }=\max _{1 \leq i \leq n}\left\{r_i\right\} \\ & r_{\min }=\min _{1 \leq i \leq n}\left\{r_i\right\} \end{aligned} $$ 以Bmax、Bmin分别表示与rmax、rmin对应的因素，则当选取Bmax、Bmin作为基点比较因素，并按9标度数值给出这个基点的相对重要程度dm后，利用下面的变换式可求得反映各因素间相对重要性程度的AHP间接判断矩阵：
$$ D=\left[\begin{array}{cccc} d_{11} & d_{12} & \cdots & d_{1 n} \\ d_{21} & d_{22} & \cdots & d_{2 n} \\ \vdots & \vdots & \vdots & \vdots \\ d_{n 1} & d_{n 2} & \cdots & d_m \end{array}\right]=\left(d_{i j}\right)_{n \times n} $$ $$ d_{i j}= \begin{cases}\frac{r_i-r_j}{r_{\max }-r_{\min }}\left(d_m-1\right)+1 & r_i-r_j \geq 0 \\ {\left[\frac{r_j-r_i}{r_{\max }-r_{\min }}\left(d_m-1\right)+1\right]^{-1}} & r_i-r_j<0\end{cases} $$ 采用ri计算式算得ri各值，列在每一比较矩阵的倒数第二列，rmax、rmin以及它们对应的Bmax、Bmin的基点相对重要性程度dm，列在每一比较矩阵的最后一列。然后利用dij计算式算得各个AHP间接判断矩阵如下：
A1—B A1 B1 B2 B3 B4 B5 B6 B7 权向量
weight vector一致性检验
consistency checkB1 1 4 1/4 1/3 3 2 1/2 0.1040 λmax=7.1952
C.I.=0.0325
R.I.=1.32
C.R.=0.0246B2 1/4 1 1/7 1/6 1/2 1/3 1/5 0.0308 B3 4 7 1 2 6 5 3 0.3517 B4 3 6 1/2 1 5 4 2 0.2412 B5 1/3 2 1/6 1/5 1 1/2 1/4 0.0449 B6 1/2 3 1/5 1/4 2 1 1/3 0.0678 B7 2 5 1/3 1/2 4 3 1 0.1596 B1—C B1 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 2/5 7/2 5/2 1 0.2078 λmax=5.0602
C.I.=0.0150
R.I.=1.12
C.R.=0.0134C2 5/2 1 5 4 5/2 0.4250 C3 2/7 1/5 1 1/2 2/7 0.0618 C4 2/5 1/4 2 1 2/5 0.0976 C5 1 2/5 2/7 5/2 1 0.2078 B2—C B2 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 3/2 2 2/3 1/2 0.1821 λmax=5.0596
C.I.=0.0149
R.I.=1.12
C.R.=0.0133C2 2/3 1 2/3 1/2 2/5 0.1122 C3 1/2 3/2 1 2/5 1/3 0.1149 C4 3/2 2 5/2 1 2/3 0.2513 C5 2 5/2 3 3/2 1 0.3395 B3—C B3 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 4 3 5 2 0.4174 λmax=5.0682
C.I.=0.0170
R.I.=1.12
C.R.=0.0152C2 1/4 1 1/2 2 1/3 0.0975 C3 1/3 2 1 3 1/2 0.1602 C4 1/5 1/2 1/3 1 1/4 0.0615 C5 1/2 3 2 4 1 0.2634 B4—C B4 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 2/5 1/2 2/3 1/3 0.0975 λmax=5.0143
C.I.=0.0036
R.I.=1.12
C.R.=0.0032C2 5/2 1 3/2 2 2/3 0.2506 C3 2 2/3 1 3/2 1/2 0.1816 C4 3/2 1/2 2/3 1 2/5 0.1317 C5 3 3/2 2 5/2 1 0.3386 B5—C B5 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 2/11 1/7 1/4 2/5 0.0435 λmax=5.1464
C.I.=0.0366
R.I.=1.12
C.R.=0.0327C2 11/2 1 2/5 5/2 4 0.2656 C3 7 5/2 1 4 11/2 0.4707 C4 4 2/5 1/4 1 5/2 0.1431 C5 5/2 1/4 2/11 2/5 1 0.0771 B6—C B6 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 1/2 2/5 1/3 2/3 0.0974 λmax=5.0143
C.I.=0.0036
R.I.=1.12
C.R.=0.0032C2 2 1 2/3 1/2 3/2 0.1817 C3 5/2 3/2 1 2/3 2 0.2506 C4 3 2 3/2 1 5/2 0.3386 C5 3/2 2/3 1/2 2/5 1 0.1317 B7—C B7 C1 C2 C3 C4 C5 权向量
weight vector一致性检验
consistency checkC1 1 1/3 3/5 1/3 1/3 0.0840 λmax=5.0080
C.I.=0.0020
R.I.=1.12
C.R.=0.0018C2 3 1 7/3 1 1 0.2654 C3 5/3 2/7 1 3/7 3/7 0.1198 C4 3 1 7/3 1 1 0.2654 C5 3 1 7/3 1 1 0.2654 2.3 由AHP间接判断矩阵计算权重[4, 8]
求解出间接判断矩阵的最大特征值λmax、C.I.及对应的特征量，将其归一化后即为某一层的有关因素相对于上一层相关因素的权重值。判断矩阵的一致性可用λmax、C.I.、R.I.和C.R.指标来检验，C.I.=(λmax-n)/(n-1)，R.I.按表 1确定，随机一致性比值C.R.=C.I./R.I.，当C. I.＜0.1时，则认为判断矩阵符合一致性要求。
表 1 平均一致性指标Table 1. The average consistency indicatorn 1 2 3 4 5 6 7 8 9 R.I. 0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 用方根法求出各个间接判断矩阵的权向量和一致性检验指标，分别列在每个间接判断矩阵的后两列。然后求出5个监测点C1、C2、C3、C4和C5对于宜渔指标A1而言，相对优劣排序及一致性检验，见表 2。
表 2 A1—B—C层次总排序Table 2. The general arrangement for layers A1—B—CA1 B1
0.1040B2
0.0308B3
0.3517B4
0.2412B5
0.0449B6
0.0678B7
0.1596层次总排序
layers sequencing一致性检验
consistency checkC1 0.2078 0.1821 0.4174 0.0975 0.0435 0.0974 0.0840 0.2195 C.I.=0.0111
R.I.=1.12
C.R.=0.0099C2 0.4250 0.1122 0.0975 0.2506 0.2656 0.1817 0.2654 0.2091 C3 0.0618 0.1149 0.1602 0.1816 0.4707 0.2506 0.1198 0.1674 C4 0.0976 0.2513 0.0615 0.1317 0.1431 0.3386 0.2654 0.1430 C5 0.2078 0.3395 0.2634 0.3386 0.0771 0.1317 0.2654 0.2610 由表 2可见，相对于宜渔指标A1这个目标而言，5个监测点C1、C2、C3、C4和C5相对优劣排序为：C5＞C1＞C2＞C3＞C4。因此，E点宜渔指标最好。
按照上面方法，分析巢湖水质指标，计算出A2—B—C层次总排序，见表 3。
表 3 A2—B—C层次总排序Table 3. The general arrangement for layers A2—B—CA2 B1
0.5690B5
0.0523B6
0.2741B8
0.0523B9
0.0523层次总排序
layers sequncing一致性检验
consistency checkC1 0.1253 0.0435 0.0615 0.0615 0.0615 0.0969 C.I.=0.0169 R.I.=1.12 C.R.=0.0151 C2 0.0613 0.1431 0.1602 0.0975 0.2634 0.1051 C3 0.4213 0.0771 0.2634 0.1602 0.4174 0.3462 C4 0.2668 0.2656 0.4174 0.4174 0.1602 0.3103 C5 0.1253 0.4707 0.0975 0.2634 0.0975 0.1415 由表 3可见，相对于水质指标A2这个目标而言，5个监测点C1、C2、C3、C4和C5相对优劣排序为：C3＞C4＞C5＞C2＞C1。因此，C点水质指标最好。
最后，求出宜渔指标A1和水质指标A2对于巢湖渔业环境优劣总目标层M的层次的排序及一致性检验，见表 4。
表 4 M—A—B—C层次总排序Table 4. The general arrangement for layers A3—B—CM A1
0.35A2
0.65层次总排序
layers sequencing一致性检验
consistency checkC1 0.2195 0.0969 0.1398 C.I.=0.01149
R.I.=1.12
C.R.=0.0133C2 0.2091 0.1051 0.1416 C3 0.1674 0.3462 0.2836 C4 0.1430 0.3103 0.2517 C5 0.2610 0.1415 0.1833 由表 4可见，相对于巢湖渔业环境优劣总目标层M而言，通过综合宜渔指标A1和水质指标A2等多因素的评判，最后得出5个监测点相对优劣总排序为：C3＞C4＞C5＞C2＞C1。因此，巢湖渔业环境C3(即监测点C)点指标最好。
3. 讨论
巢湖渔业环境5个监测点，C点渔业环境相对最好。C点水体单元位于巢湖东湖湖心，外源性污染影响较小，水域环境相对稳定，该水域同其它水域之间存在着明显的差异。从C点的生物环境来看，该点的蓝藻数量亦最低；蓝藻数量低，其对其它浮游生物的抑制作用就小，该点的生物多样性就会增加，区域内的小生境就会较其它水域好。从叶绿素a监测的结果可以看出C点的含量最低(0.094 μg · L-1)，低于一般湖泊富营养化标准值(0.1 μg · L-1)。从C点的水质环境来看，监测的17个因子中，有14个优于渔业水质标准；有3个超标，分别是总氮、总磷和石油类，该域水质总体尚可。
巢湖A点渔业环境相对最差。从A点的生物环境来看，该点的浮游生物数量和生物量都最高，其蓝藻数量也是全湖中最高的。从A点的水质环境来看，A点在巢湖的西湖区，有着众多的入湖河口，如南淝河、派河、丰乐河、杭埠河等，其中南淝河、派河向巢湖排入大量的城市污水，也是导致巢湖富营养化的主要原因之一，在水质监测结果中，A点的水质超标因子数是最多的。
监测点D、E同处巢湖的东部，巢湖地处亚热带江淮平原，夏季主导风向为东南风，处上风口；D点采样点在东口门，距柘皋河口与裕溪河口较近，E点采样点距烔炀河口较近。B点处于巢湖南部，距马尾河口不远，同D点、E点水体单元在地理、气象、水文、生物环境等方面具有较显著的相似性，仅区别于入湖径流不同。层次分析的结果说明，D点渔业环境优于E点，E点优于B点。
因此，从AHP的分析结果可以看出，巢湖水域的渔业生态环境，东湖湖心最好，东湖近岸水域次之，西湖水域最差。
-
![]()
图 1 水体中地西泮质量浓度变化特点
注：不同字母表示差异显著，后图同此。
Figure 1. Variation characteristics of diazepam mass concentration in water
Note: Different letters represent significant differences. The same case in the following figures.
![]()
图 2 底泥中地西泮质量分数变化特点
Figure 2. Variation characteristics of diazepam mass fraction in sediment
![]()
图 3 蜈蚣草中地西泮质量分数变化特点
Figure 3. Variation characteristics of diazepam mass fraction in P. vittata
表 1 流动相梯度洗脱程序
Table 1 Mobile phase gradient elution procedure
时间 t/min A/% B/% 0 95.00 5.00 1.00 95.00 5.00 2.50 5.00 95.00 3.90 5.00 95.00 3.91 95.00 5.00 5.00 95.00 5.00 
下载: 导出CSV
表 2 地西泮及内标物的质谱参数
Table 2 Mass spectrum parameters of diazepam and internal standard
化合物
Compound定性离子对
Qualitative
ion pair/
(m·z−1)定量离子对
Quantitative
ion pair/
(m·z−1)碰撞能量
Collision
energy/
(eV)地西泮
Diazepam285.2>193.1 285.2>193.1 35 285.2>154.1 37 地西泮-D5
Diazepam-D5290.2>154.1 290.2>154.1 37
下载: 导出CSV
表 3 不同基质中地西泮加标回收率和相对标准偏差
Table 3 Adding standard recovery and relative standard deviation of diazepam in different substrates
基质
Substrate加标水平
Spiked level实测结果
Measurement result回收率
Recovery rate/%相对标准偏差
RSDs/%水体 Water 0.100 μg·L−1 0.092 μg·L−1 92.0 3.831 0.600 μg·L−1 0.527 μg·L−1 87.8 3.542 1.000 μg·L−1 0.954 μg·L−1 95.4 1.555 底泥 Sediment 0.500 μg·kg−1 0.484 μg·kg−1 96.8 1.614 2.000 μg·kg−1 1.909 μg·kg−1 95.5 1.059 4.000 μg·kg−1 4.335 μg·kg−1 108.4 2.967 蜈蚣草 P. vittata 0.100 μg·kg−1 0.092 μg·kg−1 92.0 3.262 0.500 μg·kg−1 0.431 μg·kg−1 86.2 4.028 0.900 μg·kg−1 0.894 μg·kg−1 99.3 1.468
下载: 导出CSV
表 4 水体中地西泮降解动力学拟和参数
Table 4 Fitting parameters of degradation kinetics of diazepam in water
理论浓度
Theoretical concentration/
(μg·L−1)模拟养殖环境
Simulated culture
environment方程式
EquationR2 C0/
(μg·L−1)k T1/2/d 反应级数
Order of reaction0.1 μg·L−1 底泥
Sedimenty=0.001 0x+0.014 7 0.918 8 0.118 — — 零级 y=−0.011 3x−0.127 8 0.926 3 — — 一级 y=0.129 0x+1.085 8 0.932 0 0.129 0 65.69 二级 底泥-蜈蚣草
Sediment-P. vittatay=0.009 0x+0.020 9 0.950 4 0.117 — — 零级 y=−0.010 8x−0.191 5 0.959 3 — — 一级 y=0.130 9x+1.729 9 0.965 5 0.130 9 65.29 二级 1.0 μg·L−1 底泥
Sedimenty=0.004 7x+0.213 7 0.835 3 1.141 — — 零级 y=−0.0054x−0.2069 0.842 9 — — 一级 y=0.006 3x+0.200 8 0.850 3 0.006 3 139.11 二级 底泥-蜈蚣草
Sediment-P. vittatay=0.006 9x+0.231 9 0.922 5 1.142 — — 零级 y=−0.008 5x−0.224 2 0.933 7 — — 一级 y=0.010 5x+0.216 2 0.942 2 0.010 5 83.40 二级
下载: 导出CSV
表 5 底泥对不同浓度地西泮的富集系数
Table 5 Bioconcentration factors of diazepan at different concentrations in sediment
组别
Group给药时间 Time of administration/h 0 24 48 72 96 216 264 360 600 768 A组 Group A 0.65 4.46 4.73 4.93 5.38 5.87 6.92 13.26 14.54 18.80 B组 Group B 0.53 2.95 4.85 4.99 5.15 5.34 5.95 8.66 9.28 13.19 C组 Group C 1.44 5.93 6.02 6.17 6.32 6.46 7.25 7.56 9.56 9.79 D组 Group D 1.28 5.95 6.22 6.30 6.48 6.81 7.28 7.99 8.12 11.05
下载: 导出CSV
表 6 蜈蚣草对不同浓度地西泮的富集系数
Table 6 Bioconcentration factors of diazepan at different concentrations in P. vittata
组别
Group给药时间 Time of administration/h 0 24 48 72 96 216 264 360 600 768 B组 Group B 0.79 3.07 3.23 3.41 3.57 3.78 2.67 2.86 1.67 1.54 D组 Group D 0.21 0.55 0.60 0.63 0.70 0.81 0.83 0.87 0.63 0.63
下载: 导出CSV
-
[1] WANG L L, WANG R L, ZHENG Q, et al. Simulating dynamic interaction between diazepam and ethanol targeting the GABAA receptor via in silico model[J]. Neurotoxicology, 2023, 95(1): 136-143.
[2] BRODIN T, FICK J, JONSSON M, et al. Dilute concentrations of a psychiatric drug alter behavior of fish from natural populations[J]. Science, 2013, 339(6121): 814-815. doi: 10.1126/science.1226850
[3] BROOKS B W, CHAMBLISS C K, STANLEY J K, et al. Determinations of select antidepressant in fish from an effuent-dominated stream[J]. Environ Toxicol Chem, 2005, 24: 464-469. doi: 10.1897/04-081R.1
[4] JAMES S, JENNIFER J D, CUNNINGHAM C S, et al. Zebrafish behavior in novel environments effects of acute exposure to anxiolytic compounds and choice of Danio rerio line[J]. Int J Comp Psychol, 2010, 23(1): 43-61.
[5] LAURA M, ROBERTO M, CARMELINA I, et al. Simultaneous analysis of diazepam and its metabolites in rat plasma and brain tissue by HPLC-UV and SPE[J]. Talanta, 2009, 80(1): 279-285. doi: 10.1016/j.talanta.2009.06.074
[6] 吴敏. 地西泮药物污染对斑马鱼神经行为毒性及机制研究[D]. 镇江: 江苏大学, 2021: 2-4. [7] 易小翠, 易伟, 雷霖, 等. 液质联用同时测定大鼠尿液中6种苯二氮卓类药物[J]. 应用化学, 2022, 39(2): 340-348. [8] 何连军, 王鼎南, 张宜明, 等. 通过型固相萃取-高效液相色谱-串联质谱法同时测定水产品中的5种硝基咪唑和地西泮[J]. 核农学报, 2021, 35(8): 1865-1874. [9] 张璇, 杨光昕, 孔聪, 等. 高效液相色谱-串联质谱法测定水产品中镇静剂及其代谢物残留[J]. 分析化学, 2021, 49(3): 460-469. [10] 原帅, 于治国, 王海峰, 等. 城市生活污水中阿片类、苯丙胺类以及苯二氮卓类滥用物质的高分辨质谱筛选及确证[J]. 质谱学报, 2021, 42(6): 1080-1090. [11] 张彪, 敖沛尧, 靳浩然, 等. SPE−UPLC测定血液中苯二氮卓类药物[J]. 锦州医科大学学报, 2019, 40(5): 15-17, 116-117. [12] 徐越, 吴永富, 邹波, 等. 自动固相萃取-气相色谱-串联质谱法分析血液中的2'-氯地西泮[J]. 刑事技术, 2021, 46(3): 269-272. [13] 刘燕, 李蒙, 高静, 等. HPLC法测定地西泮直肠凝胶剂的药物含量及有关物质[J]. 国际药学研究杂志, 2020, 47(4): 312-317, 322. [14] 徐佳雯, 李尚, 张彦卓, 等. HPLC法同时测定地西泮直肠凝胶中地西泮、苯甲酸、苯甲醇含量[J]. 药学与临床研究, 2020, 28(2): 97-100. [15] 桑丽雅, 陈笑笑, 王扬, 等. 基于免疫磁珠的胶体金免疫层析法快速检测水产品中地西泮残留[J]. 食品工业科技, 2020, 41(20): 255-260, 284. [16] 沈可伊, 邹晓霜, 王军. 高效液相色谱−串联质谱测定虾肉中四种兽药残留及其热稳定性分析[J]. 食品与发酵工业, 2022, 48(22): 263-268. [17] AITOR S S, ALBERT E T F, ARMENTA S, et al. Molecularly imprinted polymerstir bar sorptive extraction of diazepam from natural water[J]. Microchem J, 2023, 186: 108354. doi: 10.1016/j.microc.2022.108354
[18] 中华人民共和国农业农村部. 农业农村部关于监督抽查发现的27批次问题农产品情况的通告(2022年3号)[EB/OL]. [2022-07-13]. http://www.moa.gov.cn/xw/bmdt/202207/t20220713_6404619.Htm. [19] LAGESSON A, BRODIN T, FAHLMAN J, et al. No evidence of increased growth or mortality in fish exposed to oxazepam in semi-natural ecosystems[J]. Sci Total Environ, 2018, 615: 608-614. doi: 10.1016/j.scitotenv.2017.09.070
[20] KE C L, LIU Q, LI L, et al. Residual levels and risk assessment of eugenol and its isomers in fish from China markets[J]. Aquaculture, 2018, 484: 338-342. doi: 10.1016/j.aquaculture.2017.07.034
[21] 徐鹏, 张紫英, 李文红, 等. 绿狐尾藻和空心菜对模拟池塘养殖尾水的净化效果分析[J]. 南方农业学报, 2022, 53(10): 2812-2820. [22] 黄晓丽, 白淑艳, 黄丽, 等. 空心菜浮床栽培对寒冷地区养殖水体的净化效果[J]. 贵州农业科学, 2021, 49(1): 83-87. [23] 黄晓丽, 黄丽, 高磊, 等. 空心菜对水中3种除草剂的去除作用[J]. 生态毒理学报, 2020, 15(6): 334-343. [24] 刘抗旱, 郑刘根, 张理群, 等. 复合型植物源活化剂强化蜈蚣草修复砷污染土壤的效应研究[J]. 生态环境学报, 2023, 32(3): 635-642. [25] MA L Q, KOMAR K M, TU C, et al. A fern that hyperaccumulates arsenic[J]. Nature, 2001, 409(6820): 579. doi: 10.1038/35054664
[26] OGGIER D M, WEISBROD C J, STOLLER A M, et al. Effects of diazepam on gene expression and link to physiological effects in different life stages in zebrafish Danio rerio[J]. Environ Sci Technol, 2010, 44(19): 7685-7691. doi: 10.1021/es100980r
[27] 孙翔. 六种水生植物对水体重金属的净化能力研究[D]. 淮南: 安徽理工大学, 2020: 6-8. [28] 孙世东, 赵文红, 任顺成. 直链淀粉-番茄红素复合物的光稳定性及降解动力学研究[J]. 河南工业大学学报(自然科学版), 2023, 44(4): 26-34. [29] 宋延斌, 王喜宽, 夏炎, 等. 河南洛阳市土壤和农作物中硒分布及富集特征[J]. 岩矿测试, 2022, 41(4): 652-662. [30] 丁洋. 青藏高原东缘土壤中典型持久性有机污染物的来源与迁移转化机制[D]. 武汉: 中国地质大学, 2021: 4. [31] 方龙香, 宋超, 范立民, 等. 基于正交实验设计的磺胺甲恶唑在渔业水体中的消解动态规律[J]. 中国农学通报, 2019, 35(27): 146-152. [32] CHARLES E W, STEVEN J R. Aqueous photo transformation of diazepam and related human metabolites under simulated sunlight[J]. Environ Sci Technol, 2012, 46(9): 4749-4756. doi: 10.1021/es203529z
[33] LIU Q Z, WANG L, XU X, et al. Antiepileptic drugs in aquatic environments: occurrence, toxicity, transformation mechanisms and fate. [J] Crit Rev Env Sci Tec, 2023, 407: 1-25.
[34] ROSSI I B, ADRIANA C V, PUPO R F N. Zero valent iron mediated degradation of the pharmaceutical diazepam[J]. Chemosphere, 2012, 88(6): 688-692. doi: 10.1016/j.chemosphere.2012.03.077
[35] 张超莹, 郑西来, 陈蕾, 等. 水库沉积物中铁、锰季节性释放的实验研究[J]. 水资源保护, 2013, 29(3): 79-82, 86. [36] 孙楠, 蔡振兴, 祁博伟, 等. 稻蟹共作模式下生物对多环芳烃的富集机制[J]. 东北农业大学学报, 2022, 53(9): 80-89. [37] 张淑琴. 月季根系分泌物促进根际土壤有机氯农药降解研究[J]. 环境科学与技术, 2022, 45(1): 145-153. [38] 郭思宇. 蜈蚣草、龙葵与玉米不同间作距离对镉砷复合污染农田土壤修复的影响[D]. 昆明: 昆明理工大学, 2021: 25-63. [39] 陈同斌, 韦朝阳, 黄泽春, 等. 砷超富集植物蜈蚣草及其对砷的富集特征[J]. 科学通报, 2002(3): 207-210. [40] 刘吉. 锑胁迫下蜈蚣草根系分泌物对其吸收累积锑的影响研究[D]. 贵阳: 贵州大学, 2021: 12-48. [41] 马生健, 宗久明, 曾富华, 等. 高羊茅、假俭草对除草剂与真菌病抗性研究[J]. 湛江师范学院学报, 2006(3): 78-82. [42] 周品成, 刘希强, 康兴生, 等. 4种水生植物对兽用抗生素去除效果比较[J]. 华南农业大学学报, 2019, 40(6): 67-73. [43] 郭金鹏, 卢少勇, 杨海燕, 等. 不同湿地植物多环芳烃含量及其对湿地多环芳烃去除量的贡献研究[J]. 环境工程, 2023, 41(S1): 503-508. -
期刊类型引用(1)
1. 杨光昕，张骏宇，夏薇，汪珑珑，沈晓盛，樊成奇，田晓清，孔聪. 垂钓饵料中地西泮在鲫鱼体内代谢及组织分布研究. 食品安全质量检测学报. 2025(01): 119-126 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 166
- HTML全文浏览量: 30
- PDF下载量: 48
- 被引次数: 1
粤公网安备 44010502001741号
