Study on fishery resource assessment of Pacific saury by length-based cohort analysis
-
摘要:
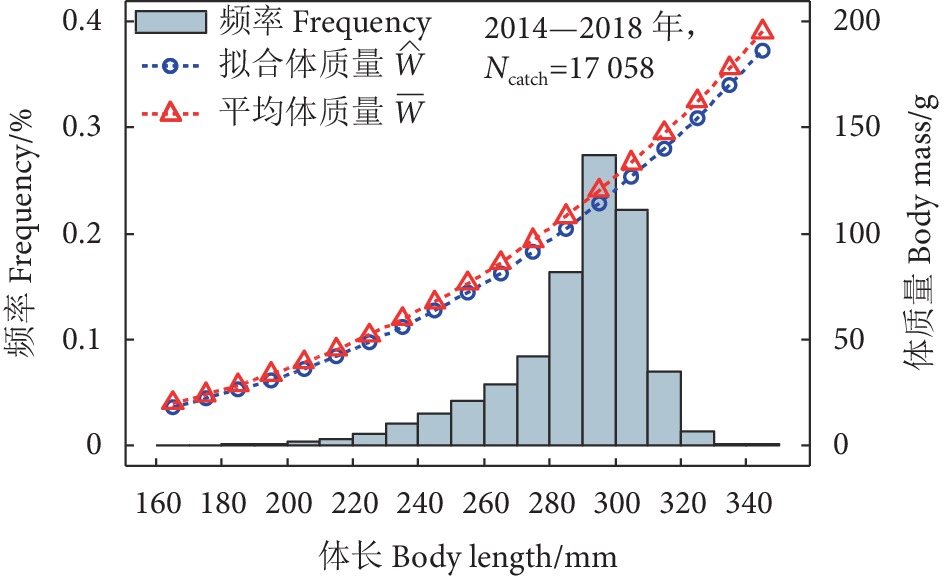
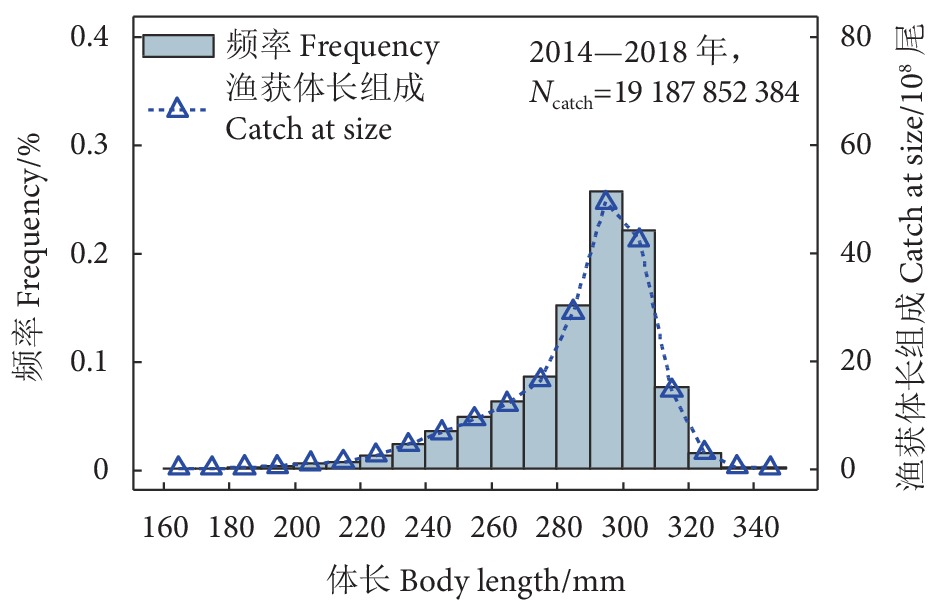
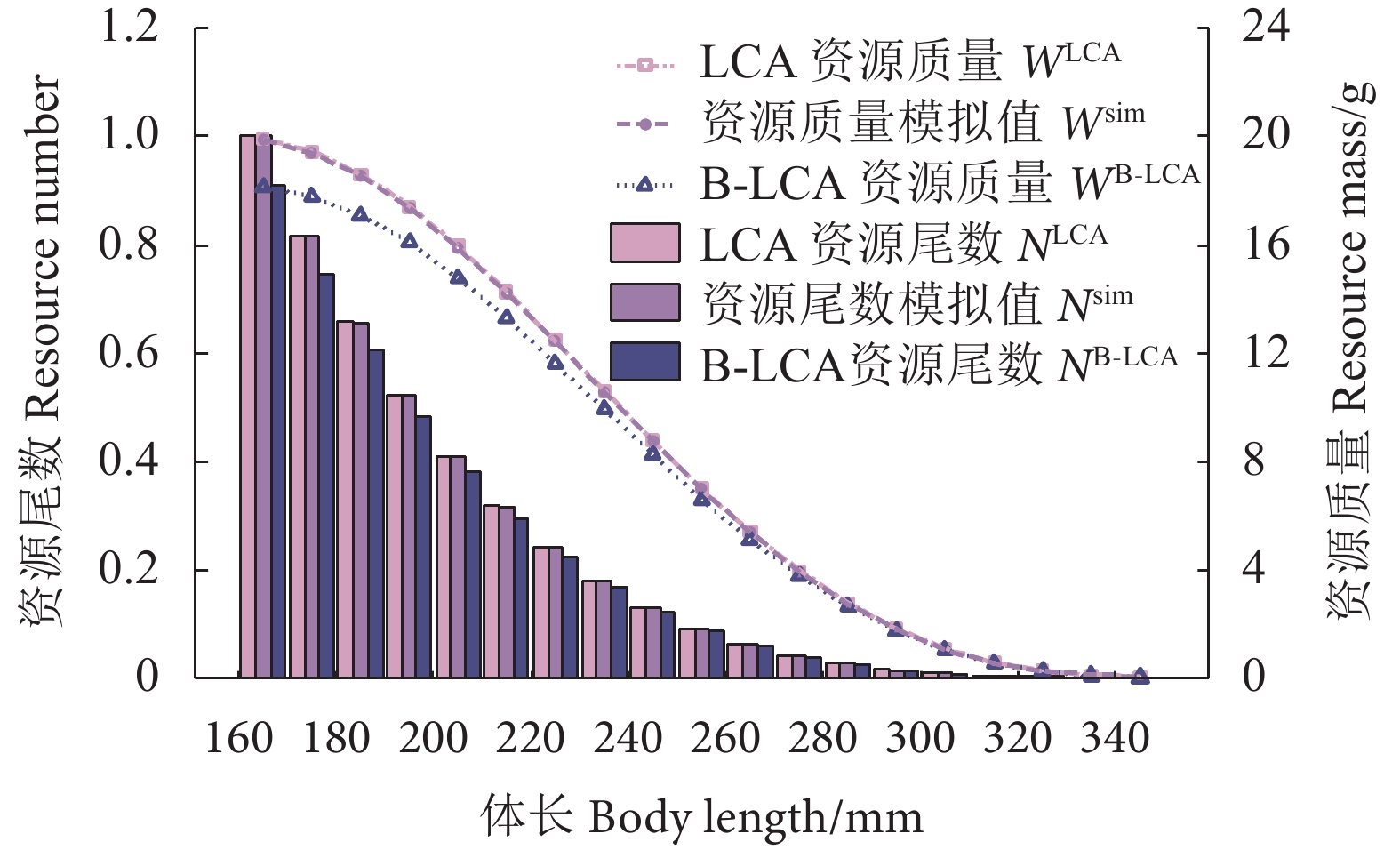
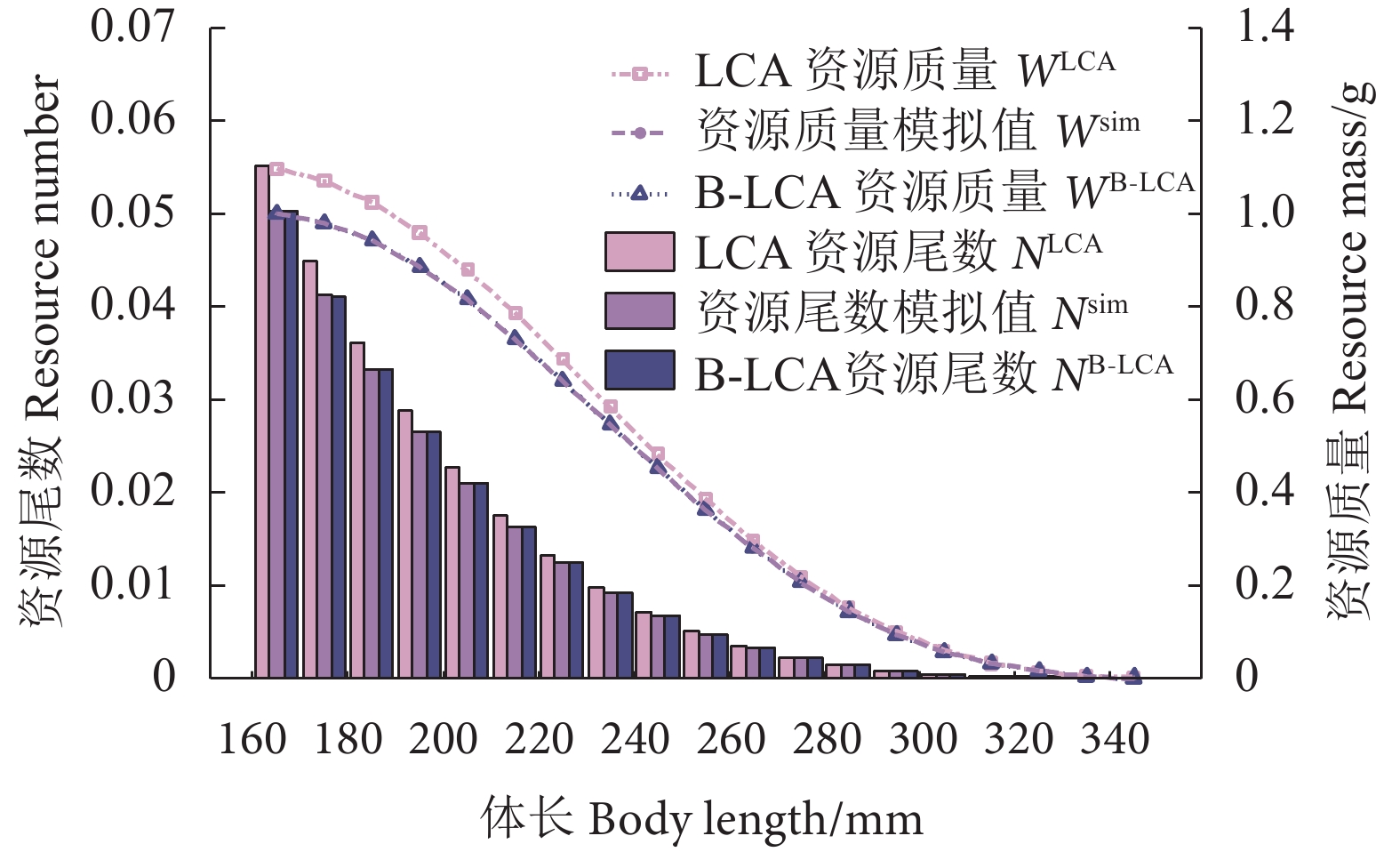
秋刀鱼 (Cololabis saira) 分布于西北太平洋亚热带到温带海域，是中国远洋渔业主要的捕捞对象之一。为探究其资源状况，根据2014—2018年西北太平洋秋刀鱼的渔获体长组成和生物学数据，对体长世代分析 (Length-based cohort analysis, LCA) 模型和基于生物量的体长世代分析 (Biomass-based length-cohort analysis, B-LCA) 模型进行性能检验和敏感性分析，并利用蒙特卡洛 (Monte Carlo) 方法估算模型参数、秋刀鱼资源量、捕捞死亡系数以及最大持续产量。结果表明：1) 在5、10和15 mm体长间隔下，LCA和B-LCA模型均表现出优秀的拟合能力，且在5 mm体长间隔下，2种模型的拟合能力均更强；2) LCA模型对于以尾数为单位的渔业数据表现更佳，B-LCA模型对于以质量为单位的渔业数据表现更佳；3) LCA和B-LCA模型对生长因子(b)、渐近体长(L∞)的变化均较敏感，且对b的敏感程度更高；4) LCA模型估算的2014—2018年秋刀鱼平均资源质量约为65.93×104~171.51×104 t，捕捞死亡系数为0.529 2，最大持续产量为37.73×104 t，而B-LCA模型估算的平均资源质量约为47.88×104~126.25×104 t，捕捞死亡系数为0.540 5，最大持续产量为33.02×104 t。2种模型估算的最大持续产量均低于北太平洋渔业委员会 (North Pacific Ocean Commission, NPFC)各成员国年均产量 (40.98×104 t)，表明2014—2018年秋刀鱼资源处于过度捕捞状态。
Abstract:Being one of the primary fishing targets in Chinese pelagic fishing, Pacific saury (Cololabis saira) is distributed in the subtropical to temperate waters of the northwest Pacific Ocean. In order to explore its resource status, according to the catch at size and biological data of Northwest Pacific saury from 2014 to 2018, we conducted a performance test and a sensitivity analysis on length-based cohort analysis (LCA) model and biomass-based length-cohort analysis (B-LCA) model. Besides, we applied Monte Carlo method to estimate the model parameters, resource quantity, fishing mortality coefficients and maximum sustainable yield of Pacific saury. The results show that: 1) The LCA model and B-LCA model exhibited excellent fitting abilities at 5, 10 and 15 mm length intervals, with stronger fitting abilities at 5 mm interval. 2) LCA model performed better for fishery data in units of number, while B-LCA model performed better for fishery data in units of mass. 3) Both LCA and B-LCA models were sensitive to changes in growth factor ($ b $) and asymptote length ($ {L}_{\infty } $), with higher sensitivity to b. 4) The average resource mass of Pacific saury from 2014 to 2018 estimated by LCA model was about 65.93×104−171.51×104 t; the fishing mortality coefficient was 0.529 2; the maximum sustainable yield was 37.73×104 t. The average resource mass estimated by B-LCA model was about 47.88×104−126.25×104 t; the fishing mortality coefficient was 0.540 5; the maximum sustainable yield was $ 33.02\times {10}^{4} $ t. The maximum sustained production estimated by both models was lower than the average annual production of NPFC (North Pacific Ocean Commission) member countries ($ 40.98\times {10}^{4} $ t), indicating that the Pacific saury resources had been overfished from 2014 to 2018.
-
Keywords:
- Cololabis saira /
- Catch at size /
- LCA model /
- B-LCA model /
- Resource quantity /
- Maximum sustainable yield
-
镉(Cd)是一种广泛存在的环境污染物，对动物和人体产生严重的毒性效应，其毒性已引起国内外学者和各国政府的广泛关注。Cd被联合国环境规划署列为首位具有全球性意义的危险性物质，被国际癌症研究机构确定为人类和实验动物的肺癌和前列腺癌的确认致癌物，美国将其列为第6位危及人类健康的有毒物质[1]。
贝类产品中蛋白质、微量元素等营养物质含量高，而且具有独特的风味、食用方便，备受世界各国消费者的青睐。多年来中国海水养殖贝类产量居世界前列，在世界水产品生产和贸易中占有重要位置。根据最新的渔业统计数据，牡蛎、蛤、扇贝和贻贝等品种占中国贝类养殖总产量的60%以上，在华南沿海的广东和广西2个省(区)，牡蛎、蛤和贻贝3个品种占海水贝类养殖总产量的75%以上。贝类对Cd有极强的累积能力，受养殖海域环境的影响，贝类体w(Cd)较高[2-5]，甚至影响到贝类产品的安全消费。许多学者对贝类体w(Cd)与安全性等进行了调查和研究，采用质量标准与质量指数等方法评价贝类产品质量[6-9]。这些评估方法算法原理简单、易于理解，对数据质量和数量要求较低，评估结果除暴露量等数值外，几乎不能提供其他信息，而且容易过高地估计暴露量结果。笔者根据广东、广西沿海的长牡蛎(Crassostrea gigas)、翡翠贻贝(Perna viridis)、文蛤(Meretrix meretrix)和菲律宾蛤仔(Ruditapes philiparum)等4种贝类w(Cd)抽样调查结果，采用随机模拟的概率评估方法，对7个年龄段人群按性别分组，对贝类Cd的膳食暴露量进行评估，以期为贝类的生产管理和安全消费提供有益的参考。
1. 材料与方法
1.1 样品采集
2009年在广东、广西沿海主要贝类养殖区采集长牡蛎、翡翠贻贝、文蛤和菲律宾蛤仔等贝类样品共140个。所有样品均采集成体，现场用海水将外壳冲洗干净，取出软体组织放于洁净的塑料袋中，冰冻保存带回实验室。
1.2 样品测定
样品解冻后用匀浆机将样品制成匀浆。样品消解按《食品卫生检测方法理化部分》(GB/T 5009.15-2003)规定，采用干法消解。检测仪器为日立公司生产的Z-2000型塞曼效应原子吸收分光光度计。所有样品平行双样检测结果的相对偏差小于10%，样品的回收率为93%~105%。
1.3 膳食暴露量评估方法
暴露量的基本计算公式[10]为：
$$ E=C \times I r / B w $$ (1) 式中E表示Cd的膳食暴露量，是以单位体质量表示的消费者每日摄入Cd的数量(g · kg-1)；C表示贝类体w(Cd)(mg · kg-1)；Ir表示贝类的每日消费量(g)；Bw表示消费者体质量(kg)。对于重金属等具有累积性的有害物质，通常采用暂定每周耐受摄入量(PTWI)来评估消费者摄入安全性，笔者将上述暴露量计算公式调整为：
$$ E=7 \times C \times I r / B w $$ (2) 1.4 评估的算法
采用基于概率分布的评估法[11-12]，用概率分布来描述式(2)中的变量。由于贝类体w(Cd)的数据量较少，此文采取参数方法。利用现有数据建立贝类体Cd的概率分布模型，依模型进行随机抽样，代入式(2)，计算出相应的暴露量。模型实现过程如下。
1) 根据式(2)中各变量的原始数据，将其分别定义成概率分布，参加抽样。进行n次随机抽样，按式(2)计算出n个暴露量值，并统计这n个数的均值、百分位数等统计量，描述变量的变异性。
2) 对上述过程重复m次，统计每一次所得的均值、百分位数等统计量，计算经过m次重复后各个统计量的置信区间，描述统计量的不确定性。
1.5 暴露评估其他数据的取值
暴露量评估中消费者体质量和贝类消费量数据参考广东省居民膳食结构调查和中国总膳食调查等资料[10, 13-14]。为区分人群特征，对数据进行整合，确定其基本取值(表 1)。
表 1 目标人群的体质量和贝类的日消费量Table 1. Body weight of target population and daily consumption of shellfish年龄
age体质量/kg body weight 消费量/g consumption 男 male 女 female 男 male 女 female 4~6 18.2 17.6 10.5 10.0 7~10 26.0 25.1 16.7 11.5 11~14 36.2 36.4 26.8 17.5 15~17 50.6 47.8 42.5 33.2 18~40 63.4 54.3 34.1 31.0 40~60 62.7 56.6 26.3 25.5 >60 60.5 53.5 29.0 24.4 2. 结果与分析
2.1 贝类体w(Cd)特征
由于贝类对Cd等重金属有较强的富集能力，所有样品中均检测到Cd的存在(表 2)。与无公害食品水产品中有毒有害物质限量(NY 5073-2006)值相比，文蛤、翡翠贻贝、菲律宾蛤仔和长牡蛎样品中w(Cd)全部低于限量标准值，符合无公害水产品质量要求。
表 2 贝类体w(Cd)的检测结果Table 2. Content of cadmium in shellfish samplesmg · kg-1 种类
species范围
range平均值
mean中值
median偏度
skewness峰度
kurtosis文蛤(Meretrix meretrix) 0.08~0.22 0.16 0.16 －0.290 －0.453 翡翠贻贝(Perna viridis) 0.21~0.39 0.29 0.27 0.773 －0.489 菲律宾蛤仔(Ruditapes philippinarum) 0.10~0.72 0.32 0.14 0.588 －1.739 长牡蛎(Crassostrea gigas) 0.31~0.76 0.47 0.44 0.733 －0.445 统计结果表明，长牡蛎样品w(Cd)显著高于其他3种贝类(P < 0.05，下同)，而文蛤样品w(Cd)显著低于其他3种贝类，翡翠贻贝和菲律宾蛤仔样品中w(Cd)没有显著性差异。文蛤、翡翠贻贝和长牡蛎样品中w(Cd)的平均值与中值一致，偏度、峰度系数接近于0(表 2)，w(Cd)符合正态分布。对于所有贝类样品，w(Cd)经过对数变换后符合对数正态分布。贝类体w(Cd)检测数据质量较好，不存在大量偏低(如未检出)或偏高的异常值，符合膳食暴露量评估的基本要求。
2.2 贝类体Cd的膳食暴露量
WHO/FAO的食品添加剂联合专家委员会(JECFA)推荐的Cd暂定PTWI为7 g · kg-1。根据随机模拟的算法，高百分位数(P95)下贝类Cd的膳食暴露量占PTWI的29.1%~57.4%。从单一食品角度看，贝类中Cd的膳食暴露风险在可接受范围内(表 3)。
表 3 目标人群的贝类Cd膳食周暴露量的估计值Table 3. Estimated weekly dietary exposure to cadmium in shellfish for target population年龄
age性别
sex平均值
average众数
mode百分位数估计值* perentile estimate 点估计
P.E.P50 P75 P90 P95 4~ 6 男 1.22 0.43 1.05 1.73 2.27 2.51 3.38 (0.97~1.11) (1.59~1.82) (2.09~2.39) (2.31~2.64) 女 1.33 0.45 1.15 1.89 2.50 2.70 3.50 (1.08~1.21) (1.77~1.99) (2.34~2.64) (2.53~2.85) 7~ 10 男 1.65 0.56 1.45 2.32 3.09 3.33 4.17 (1.29~1.56) (2.06~2.49) (2.74~3.32) (2.95~3.57) 女 1.10 0.39 0.95 1.56 2.07 2.24 2.82 (0.56~1.02) (1.42~1.68) (1.88~2.23) (2.03~2.42) 11~14 男 1.70 0.58 1.48 2.38 3.15 3.49 4.49 (1.38~1.56) (2.22~2.50) (2.94~3.32) (3.25~3.67) 女 1.16 0.41 1.02 1.62 2.14 2.37 3.12 (0.92~1.08) (1.47~1.73) (1.94~2.28) (2.14~2.51) 15~17 男 1.99 0.68 1.75 2.85 3.66 4.02 5.17 (1.61~1.83) (2.63~2.98) (3.38~3.83) (3.71~4.21) 女 1.70 0.58 1.45 2.44 3.19 3.51 4.40 (1.35~1.53) (2.26~2.57) (2.96~3.36) (3.26~3.70) 18~40 男 1.28 0.44 1.11 1.84 2.37 2.61 3.31 (1.04~1.18) (1.71~1.95) (2.21~2.51) (2.43~2.77) 女 1.38 0.47 1.22 1.97 2.58 2.84 3.52 (1.13~1.29) (1.84~2.09) (2.40~2.73) (2.64~3.01) 40~60 男 1.03 0.34 0.91 1.47 1.88 2.04 2.53 (0.86~0.95) (1.38~1.54) (1.76~1.96) (1.92~2.14) 女 1.09 0.37 0.95 1.57 2.02 2.19 2.78 (0.87~0.99) (1.45~1.65) (1.87~2.13) (2.02~2.30) >60 男 1.10 0.38 0.97 1.56 2.04 2.24 2.79 (0.92~1.01) (1.48~1.63) (1.93~2.13) (2.13~2.35) 女 1.12 0.38 0.99 1.60 2.03 2.21 2.81 (0.92~1.05) (1.48~1.69) (1.87~2.13) (2.05~2.33) 注：*.反映了贝类体Cd膳食暴露量的变异性；括号内为90%的置信区间，不确定性以置信区间来描述
Note: *.variability of dietary exposure to cadmium in shellfish. The values in brackets indicate 90% confidence interval that descibes uncertainty.15~17岁年龄段人群的Cd膳食暴露量最高，其次是11~14岁和7~10岁年龄段的男性人群，40~60岁年龄段人群Cd的膳食暴露量最低。7~10岁、11~14岁和15~17岁年龄段的人群，男性人群的Cd膳食暴露量高于女性；而4~6岁、18~40岁、40~60岁和60岁以上年龄段男性人群的Cd暴露量低于女性(表 3)。由暴露量计算公式可以看出，Cd的膳食暴露量与贝类日消费量正相关，而与消费者体质量成反比，暴露量随贝类每日消费量的增加而升高、随体质量增加而降低。成年人(18岁以上)膳食量与体质量相对稳定，而青少年、儿童膳食量与体质量变化大，因而未成年人Cd暴露量差值大。成年人群中不同性别体质量差值大(表 1)，Cd的膳食暴露量存在差异。
3. 讨论
食品安全风险分析中暴露评估通常采用点评估方法，暴露量计算公式中所有变量用保守的点值来描述，消费量取高百分位数值P97.5，污染物取最高含量，体质量取平均值[10, 15]，这忽略了消费量和污染物含量的变异性，容易高估暴露量而使评估结果趋于保守，是一种为保护大多数人群而采用的方法，评估结果仅提供暴露量的信息，不能描述暴露量的变异性和不确定性。概率评估是用一个概率分布来描述变量的暴露评估方法。与点估计的方法相比，概率评估通过对变量随机抽样的模拟方式，给出暴露量的概率分布，定量描述了暴露量的变异性。评价概率性模型有效的标准之一是其结果要低于点估计模型结果[15]。由于点估计模型是基于“最坏情况假设”的估计，2种模型的比较较为困难。国外研究采用概率模型暴露分布所有分位数与点估计值比较[15-16]，此文采用P95估计值与之比较。与点估计结果相比，采用随机模拟的概率评估的P95分位数估计值明显低于点估计值。由于贝类消费量和w(Cd)呈正偏态分布，其右侧尾部数据变异很大，点估计的方法采用了消费量数据的P97.5分位数和最大w(Cd)，评估结果涵盖绝大部分人群，但结果过度保守。
从评估的结果(表 3)看，各年龄、性别段人群贝类体Cd膳食暴露量的众数＜中值(P50)＜平均值，表明贝类体Cd的膳食暴露量评估结果的分布趋势呈现高度右偏，大多数出现在低暴露量区域内。在同一个年龄性别段内，贝类Cd暴露量的4个百分位数值(P50，P75，P90和P95)相差约2~3倍。这种差异是由于消费者个体数据如体质量、消费量等的差值对暴露量的影响，反映了暴露量的变异性。用随机模拟的概率方法能够有效地量化变异性[17-18]，获得贝类Cd膳食暴露量概率分布，并给出因消费者个体差异等因素而产生的暴露量差异。
风险评估中的不确定性是由于主观原因造成对客观暴露事实认知的偏差。大致可分为假设暴露情景的不确定、模型的不确定以及参数的不确定3种类型。不确定度对评估结果产生的影响大多是负面的，直接影响结果的可信度。此文的不确定性主要来源于模型和参数。在评估过程中采用随机模拟方法抽样，虽然对变异性进行了量化，但随机模拟本身也可能是不确定性的一个来源[10]。为保证评估结果的精度和准确，笔者用尽可能大的抽样次数(20 000次)和重复模拟次数(100次)以降低评估的不确定性。
研究发现，尽管贝类软组织富集Cd，却没有发现因大量食用w(Cd)高的牡蛎而出现副作用[19-20]，大量食用贝类的女性血液中w(Cd)也没有升高，而随大便排出的Cd量相当于贝类膳食中摄入Cd的99%以上，表明贝类的膳食中Cd的吸收很低[21]。由于缺乏相关资料，暴露量计算公式(1)和(2)没有考虑贝类在消费者体内的消化和吸收利用率的影响。另外，贝类的烹调等加工过程对w(Cd)所产生的影响，也是此文中贝类Cd膳食暴露量不确定的重要来源。
在对农药、重金属等化学污染物的风险评估中发现，暴露量在不同年龄、性别的人群中存在差异[22-23]，笔者通过对模拟数据的统计分析也发现类似的结果。不同年龄段人群贝类Cd的膳食暴露量呈显著性差异，各个年龄段人群Cd的膳食暴露量存在显著的性别差异。然而，这是否意味着消费者对贝类体Cd的膳食暴露量存在特别的性别指向，还需进一步的调查研究。
贝类产品Cd的膳食暴露量低于PTWI推荐值，但贝类膳食在居民总膳食中的比重较小，而贝类中Cd的膳食暴露量占PTWI的百分比较高，有必要进一步降低。贝类对Cd的富集能力强，贝类体w(Cd)受养殖海域环境的影响，需要加强对贝类养殖环境的保护，降低贝类中w(Cd)；适当减少贝类产品的膳食量，降低其膳食暴露风险。与鱼类等水产品不同，贝类的消费频率低。如果每月消费1次，18岁以上成年人消费量不超过300 g，11~17岁青少年消费量不超过250 g，儿童(小于10岁)消费量不超过100 g，将有效降低贝类体Cd的膳食暴露量。
此外，虽然采用随机模拟的概率评估方法给出了比点评估更全面、详细的信息，考虑到此研究所采集的贝类品种数和样本量相对较少，为了更准确地评估贝类Cd的膳食暴露水平，有必要进一步加大贝类的品种和样本量，使调查更具有代表性。
-
![]()
图 3 基于尾数模拟数据LCA和B-LCA模型的估算值与模拟值对比图
Figure 3. Comparison between estimated and simulated values of LCA and B-LCA models based on number-based simulated data
![]()
图 4 基于质量模拟数据LCA和B-LCA模型的估算值与模拟值对比图
Figure 4. Comparison between estimated and simulated values of LCA and B-LCA models based on mass-based simulated data
![]()
图 5 基于LCA和B-LCA模型估算的平均资源质量与捕捞死亡系数在体长组间的变化趋势
Figure 5. Trends of average resource mass and fishing mortality coefficient between body length class estimated based on LCA and B-LCA models
表 1 秋刀鱼生物学参数
Table 1 Biological parameters of Pacific saury
参数
Parameter符号
Symbol数值
Value条件因子 Condition factor a 2.468 4×10−6 生长因子 Growth factor b 3.110 7 自然死亡系数 Coefficient of natural mortality M 0.328 9 捕捞死亡系数 Coefficient of fishing mortality F 1.271 1 总死亡系数 Total mortality coefficient Z 1.600 0 渐进体长 Asymptote length L∞ 360.230 0 生长参数 Growth parameter K 0.360 0 
下载: 导出CSV
表 2 模型性能指标
Table 2 Model performance indicators
间隔
Interval/mm模拟数据
Simulated data模型
Model性能指标
Model efficiency5 基于资源尾数
Number-basedLCA 1.000 0 B-LCA 0.995 9 基于资源质量
Mass-basedLCA 0.995 5 B-LCA 1.000 0 10 基于资源尾数
Number-basedLCA 1.000 0 B-LCA 0.986 4 基于资源质量
Mass-basedLCA 0.983 3 B-LCA 1.000 0 15 基于资源尾数
Number-basedLCA 0.999 9 B-LCA 0.972 6 基于资源质量
Mass-basedLCA 0.962 7 B-LCA 1.000 0
下载: 导出CSV
表 3 敏感性分析结果
Table 3 Sensitivity analysis results
模拟数据
Simulated data参数
Parameter基准方案
Base case变化
Change敏感性方案
Sensitivity case敏感性指数
Sensitivity index$ {W}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}^{\mathrm{L}\mathrm{C}\mathrm{A}} $ $ {W}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}^{\mathrm{B}{\text{-}}\mathrm{L}\mathrm{C}\mathrm{A}} $ $ {W}_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y}}^{\mathrm{L}\mathrm{C}\mathrm{A}} $ ${W}_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y} }^{\mathrm{B}{\text{-}}\mathrm{L}\mathrm{C}\mathrm{A} }$ LCA B-LCA 基于资源尾数 a 1.604 7 1.487 2 +10% 1.765 2 1.635 9 1.000 0 0.194 6 Number-based 1.604 7 1.487 2 −10% 1.444 2 1.338 5 1.000 0 1.658 9 基于资源质量 0.088 4 0.081 9 +10% 0.088 4 0.081 9 0.000 0 −0.732 2 Mass-based 0.088 4 0.081 9 −10% 0.088 4 0.081 9 0.000 0 0.732 2 基于资源尾数 b 1.604 7 1.487 2 +10% 8.448 0 7.775 2 42.645 3 38.452 7 Number-based 1.604 7 1.487 2 −10% 0.305 6 0.285 2 8.095 7 8.222 6 基于资源质量 0.088 4 0.081 9 +10% 0.095 7 0.088 1 0.831 5 −0.031 2 Mass-based 0.088 4 0.081 9 −10% 0.081 8 0.076 4 0.744 3 1.361 1 基于资源尾数 $ K $ 1.604 7 1.487 2 +10% 1.786 5 1.657 7 1.133 1 0.330 0 Number-based 1.604 7 1.487 2 −10% 1.786 5 1.657 7 1.116 8 1.777 6 基于资源质量 0.088 4 0.081 9 +10% 0.098 4 0.091 3 1.135 2 0.331 8 Mass-based 0.088 4 0.081 9 −10% 0.098 4 0.091 3 −1.135 2 −0.331 8 基于资源尾数 $ {L}_{{\infty } } $ 1.604 7 1.487 2 +10% 2.080 8 1.935 1 2.966 7 2.058 7 Number-based 1.604 7 1.487 2 −10% NA NA NA NA 基于资源质量 0.088 4 0.081 9 +10% 0.114 7 0.106 7 2.978 2 2.069 3 Mass-based 0.088 4 0.081 9 −10% NA NA NA NA 基于资源尾数 $ M $ 1.604 7 1.487 2 +10% 1.605 3 1.487 7 0.003 5 −0.728 9 Number-based 1.604 7 1.487 2 −10% 1.604 2 1.486 7 0.003 4 0.735 4 基于资源质量 0.088 4 0.081 9 +10% 0.088 4 0.081 9 0.003 3 −0.729 2 Mass-based 0.088 4 0.081 9 −10% 0.088 4 0.081 9 0.003 1 0.735 1 基于资源尾数 $ F $ 1.604 7 1.487 2 +10% 1.764 7 1.635 5 0.997 0 0.191 8 Number-based 1.604 7 1.487 2 −10% 1.444 7 1.338 9 0.997 0 1.656 1 基于资源质量 0.088 4 0.081 9 +10% 0.081 1 0.075 1 −0.827 6 −1.507 9 Mass-based 0.088 4 0.081 9 −10% 0.097 1 0.090 1 −0.981 8 −0.192 1 注：NA表示缺失值。 Note: NA indicates missing values.
下载: 导出CSV
表 4 模型参数的后验分布
Table 4 Posterior distribution of model parameters
参数
Parameter模型
Model95%置信区间
95% confidence interval均值
Mean标准差
SD潜在尺度缩减因子
Psrf下限 Lower 上限 Uppe $ M $ LCA 0.264 13 0.392 13 0.328 93 0.032 697 1.000 1 B-LCA 0.265 26 0.394 98 0.328 75 0.033 046 1.000 0 $ F $ LCA 1.018 6 1.520 7 1.270 8 0.128 04 1.000 1 B-LCA 1.018 1 1.516 5 1.270 5 0.127 10 1.000 2 $ K $ LCA 0.292 02 0.432 27 0.360 04 0.035 822 1.000 0 B-LCA 0.288 91 0.430 53 0.360 27 0.036 064 1.000 2 $ {L}_{\infty } $ LCA 290.67 429.86 360.24 35.853 1.000 1 B-LCA 288.41 429.55 360.52 36.011 1.000 1 $ b $ LCA 2.504 2 3.729 1 3.110 8 0.311 77 1.000 1 B-LCA 2.505 1 3.722 3 3.111 2 0.310 42 1.000 0 $ a $ LCA 1.99×10−6 2.96×10−6 2.47×10−6 2.47×10−7 1.000 2 B-LCA 1.98×10−6 2.94×10−6 2.47×10−6 2.48×10−7 0.999 99
下载: 导出CSV
表 5 秋刀鱼平均资源质量、捕捞死亡系数及最大持续产量
Table 5 Average resource mass, fishing mortality coefficient and maximum sustainable yield of Pacific saury
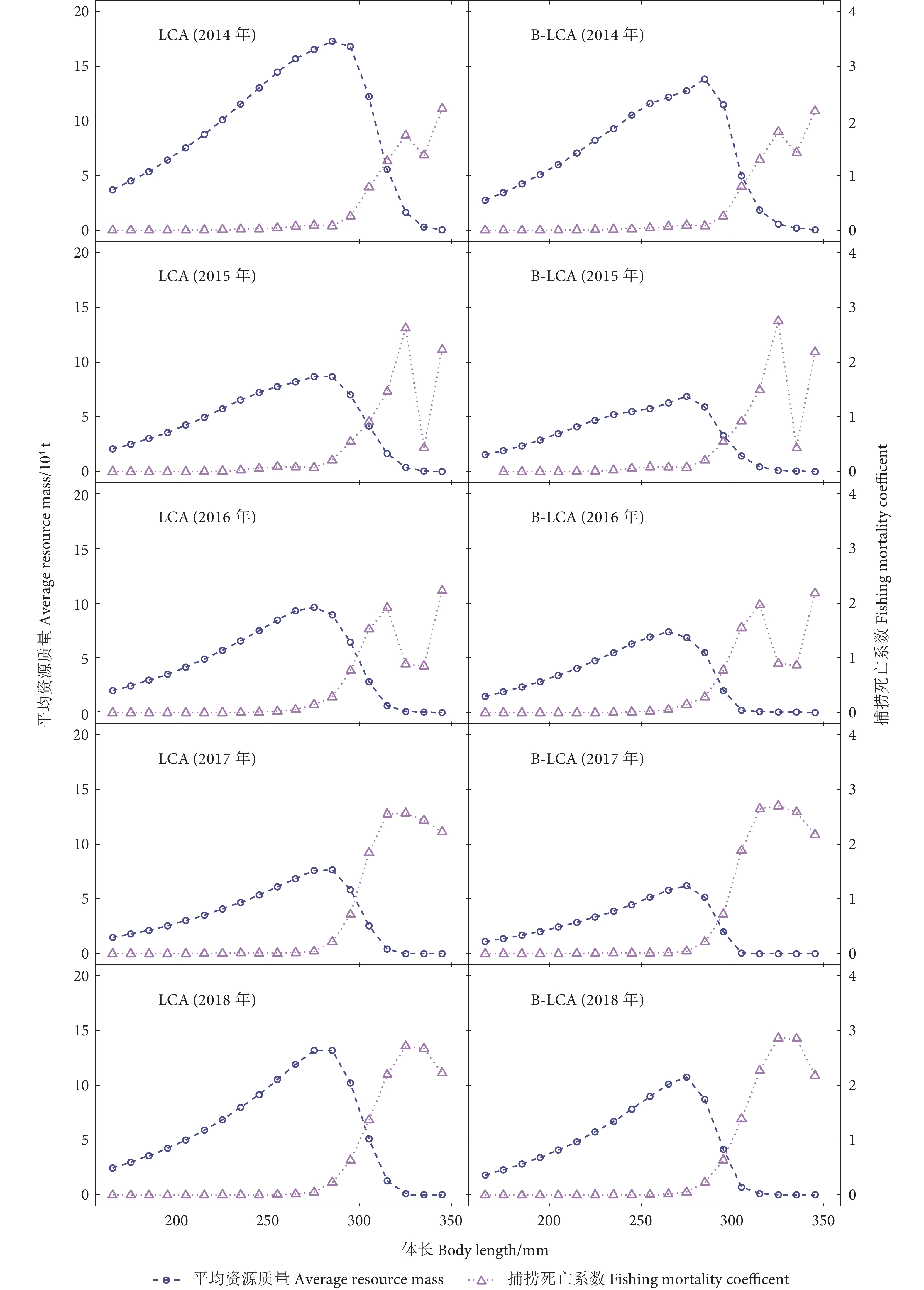
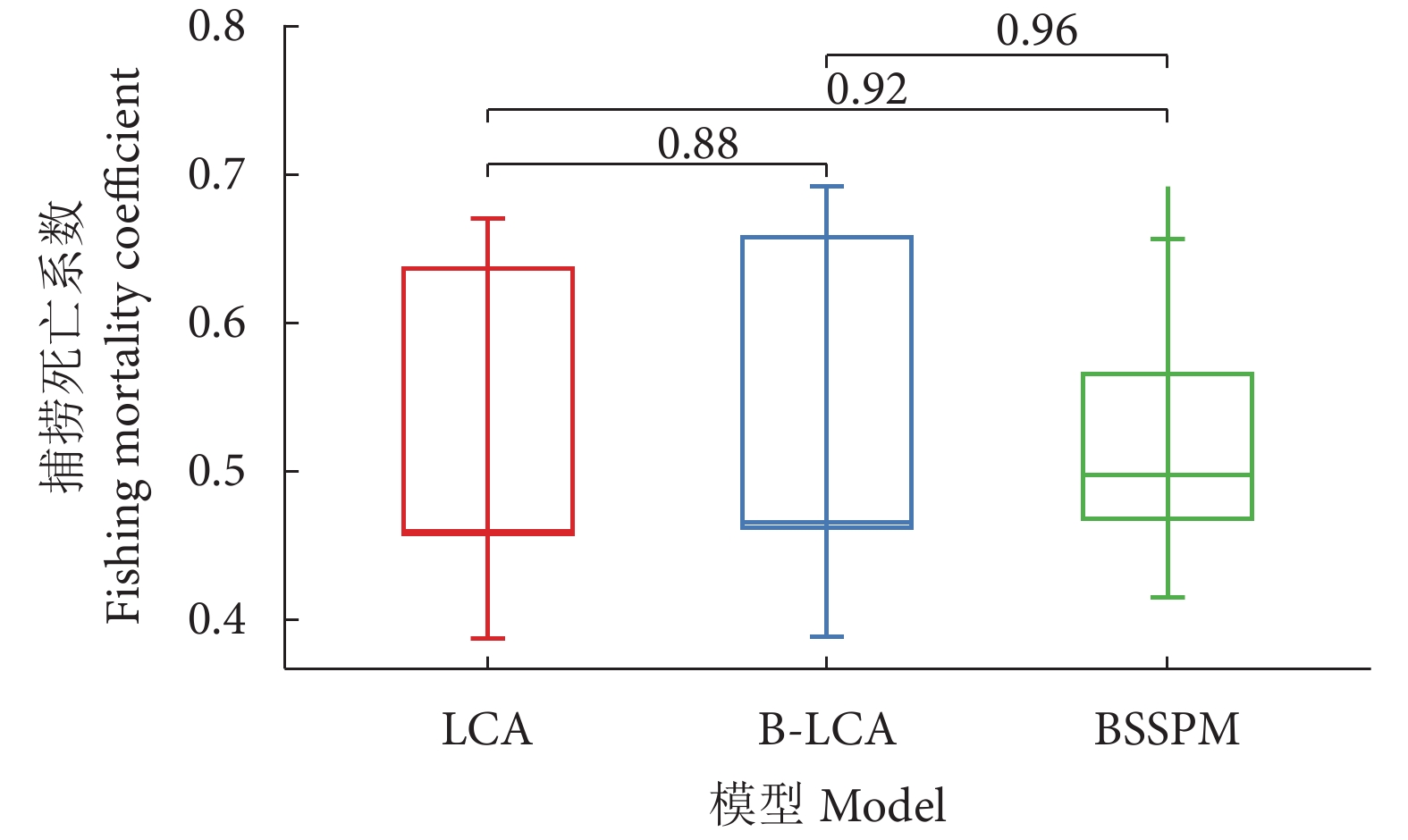
年份
Year总产量
Wtc/104 tLCA B-LCA F W/104 t W/104 t F W/104 t WMSY/104 t 2014 63.02 0.422 6 171.51 59.72 0.427 5 126.25 52.26 2015 35.89 0.459 8 86.51 32.17 0.466 4 61.81 28.11 2016 36.17 0.458 7 86.35 32.29 0.462 5 61.68 28.22 2017 26.26 0.667 5 65.93 23.97 0.687 8 47.88 21.00 2018 43.59 0.637 6 113.86 40.52 0.658 1 83.29 35.49 均值 Mean 40.99 0.529 2 104.83 37.73 0.540 5 76.18 33.02
下载: 导出CSV
-
[1] IWAHASHI M, ISODA Y, ITO S I, et al. Estimation of seasonal spawning ground locations and ambient sea surface temperatures for eggs and larvae of Pacific saury (Cololabis saira) in the western North Pacific[J]. Fish Oceanogr, 2006, 15(2): 125-138. doi: 10.1111/j.1365-2419.2005.00384.x
[2] 王茜, 崔雪森. 国际渔业动态[J]. 渔业信息与战略, 2020, 35(4): 327-332. [3] 史登福, 张魁, 陈作志. 基于生活史特征的数据有限条件下渔业资源评估方法比较[J]. 中国水产科学, 2020, 27(1): 12-24. [4] COSTELLO C, OVANDO D, HILBORN R, et al. Status and solutions for the world's unassessed fisheries[J]. Science, 2012, 338(6106): 517-520. doi: 10.1126/science.1223389
[5] HORDYK A, ONO K, VALENCIA S, et al. A novel length-based empirical estimation method of spawning potential ratio (SPR), and tests of its performance, for small-scale, data-poor fisheries[J]. ICES J Mar Sci, 2015, 72(1): 217-231. doi: 10.1093/icesjms/fsu004
[6] RUDD M B, THORSON J T. Accounting for variable recruitment and fishing mortality in length-based stock assessments for data-limited fisheries[J]. Can J Fish Aquat Sci, 2018, 75(7): 1019-1035. doi: 10.1139/cjfas-2017-0143
[7] WANG J T, YU W, CHEN X J, et al. Stock assessment for the western winter-spring cohort of neon flying squid (Ommastrephes bartramii) using environmentally dependent surplus production models[J]. Sci Mar, 2016, 80(1): 69-78.
[8] TRUESDELL S B, BENCE J R, SYSLO J M, et al. Estimating multinomial effective sample size in catch-at-age and catch-at-size models[J]. Fish Res, 2017, 192: 66-83. doi: 10.1016/j.fishres.2016.11.003
[9] JONES R. Assessing the long-term effects of changes in fishing effort and mesh size from length composition data[J]. ICES J Mar Sci, 1974, 33: 1-13.
[10] 詹秉义. 渔业资源评估[M]. 北京: 中国农业出版, 1995: 312-314. [11] 周永东, 徐汉祥. 应用体长股分析法估算东海海鳗资源量[J]. 浙江海洋学院学报(自然科学版), 2007, 26(4): 399-403. [12] 周永东, 张洪亮, 徐汉祥, 等. 应用体长股分析法估算东海区日本鲭资源量[J]. 浙江海洋学院学报(自然科学版), 2011, 30(2): 91-94. [13] 吴斌, 方春林, 贺刚, 等. 运用体长股法初步估算湖口江段短颌鲚资源量[J]. 湖北农业科学, 2014, 53(16): 3866-3869. [14] ZHANG C I, SULLIVAN P J. Biomass-based cohort analysis that incorporates growth[J]. Trans Am Fish Soc, 1988, 117(2): 180-189. doi: 10.1577/1548-8659(1988)117<0180:BBCATI>2.3.CO;2
[15] ZHANG C I, MEGREY B A. A simple biomass-based length-cohort analysis for estimating biomass and fishing mortality[J]. Trans Am Fish Soc, 2010, 139(3): 911-924. doi: 10.1577/T09-041.1
[16] 朱清澄, 花传祥. 西北太平洋秋刀鱼渔业[M]. 北京: 海洋出版社, 2017: 1-2. [17] TAMURA T, FUJISE Y. Geographical and seasonal changes of the prey species of minke whale in the Northwestern Pacific[J]. ICES J Mar Sci, 2002, 59(3): 516-528. doi: 10.1006/jmsc.2002.1199
[18] SHIMIZU Y, TAKAHASHI K, ITO S I, et al. Transport of subarctic large copepods from the Oyashio area to the mixed water region by the coastal Oyashio intrusion[J]. Fish Oceanogr, 2009, 18(5): 312-327. doi: 10.1111/j.1365-2419.2009.00513.x
[19] SMITH A D, BROWN C J, BULMAN C M, et al. Impacts of fishing low-trophic level species on marine ecosystems[J]. Science, 2011, 333(6046): 1147-1150. doi: 10.1126/science.1209395
[20] PIKITCH E K, ROUNTOS K J, ESSINGTON T E, et al. The global contribution of forage fish to marine fisheries and ecosystems[J]. Fish Fish, 2014, 15(1): 43-64. doi: 10.1111/faf.12004
[21] North Pacific Fisheries Commission. 7th Meeting Report[R]. Tokyo: NPFC, 2022.
[22] NAKAYA M, MORIOKA T, FUKUNAGA K, et al. Growth and maturation of Pacific saury Cololabis saira under laboratory conditions[J]. Fish Sci, 2010, 76: 45-53. doi: 10.1007/s12562-009-0179-9
[23] BAITALIUK A, ORLOV A, ERMAKOV Y K. Characteristic features of ecology of the Pacific saury Cololabis saira (Scomberesocidae, Beloniformes) in open waters and in the northeast Pacific Ocean[J]. J Ichthyol, 2013, 53(11): 899-913. doi: 10.1134/S0032945213110027
[24] 朱清澄, 杨明树, 高玉珍, 等. 西北太平洋秋刀鱼耳石生长与性成熟度、个体大小的关系[J]. 上海海洋大学学报, 2017, 26(2): 263-270. [25] KIMURA N, OKADA Y, MAHAPATRA K. Relationship between saury fishing ground and sea surface oceanographic features determined from satellite data along the northeastern coast of Japan[J]. J Mar Sci Technol, 2004, 2(2): 1-12.
[26] 张孝民, 石永闯, 李凡, 等. 基于MAXENT模型预测西北太平洋秋刀鱼潜在渔场[J]. 上海海洋大学学报, 2020, 29(2): 280-286. [27] 张培超, 张孝民, 陈丙见, 等. 北太平洋秋刀鱼渔场与水温垂直结构的关系[J]. 河北渔业, 2022(6): 35-39, 44. [28] 谢斌, 汪金涛, 陈新军, 等. 西北太平洋秋刀鱼资源丰度预报模型构建比较[J]. 广东海洋大学学报, 2015, 35(6): 58-63. [29] 朱文涛, 陈新军, 汪金涛, 等. 基于灰色系统的西北太平洋秋刀鱼资源丰度预测[J]. 广东海洋大学学报, 2018, 38(6): 13-17. [30] 孟令文, 朱清澄, 花传祥, 等. 栖息地指数模型在北太公海秋刀鱼渔情预报中的应用[J]. 海洋湖沼通报, 2018(6): 142-149. doi: 10.13984/j.cnki.cn37-1141.2018.06.019 [31] 许巍, 朱清澄, 张先存, 等. 西北太平洋秋刀鱼舷提网捕捞技术[J]. 齐鲁渔业, 2005, 22(10): 43-45. [32] 石永闯, 朱清澄, 张衍栋, 等. 基于模型试验的秋刀鱼舷提网纲索张力性能研究[J]. 中国水产科学, 2016, 23(3): 704-712. [33] PAULY D. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks[J]. ICES J Mar Sci, 1980, 39(2): 175-192. doi: 10.1093/icesjms/39.2.175
[34] ALLEN M S, WALTERS C J, MYERS R. Temporal trends in largemouth bass mortality, with fishery implications[J]. N Am J Fish Manag, 2008, 28(2): 418-427. doi: 10.1577/M06-264.1
[35] HUGHES S E. Stock composition, growth, mortality, and availability of Pacific saury, Cololabis saira, of the northeastern Pacific Ocean[J]. Fish Bull, 1974, 72(1): 121-131.
[36] GUPTA H V, KLING H, YILMAZ K K, et al. Decomposition of the mean squared error and NSE performance criteria: implications for improving hydrological modelling[J]. J Hydrol, 2009, 377(1/2): 80-91.
[37] MORIASI D N, GITAU M W, PAI N, et al. Hydrologic and water quality models: performance measures and evaluation criteria[J]. Transactions of ASABE, 2015, 58(6): 1763-1785. doi: 10.13031/trans.58.10715
[38] SUN X, NEWHAM L T, CROKE B F, et al. Three complementary methods for sensitivity analysis of a water quality model[J]. Environ Model Softw, 2012, 37: 19-29. doi: 10.1016/j.envsoft.2012.04.010
[39] PLUMMER M, BEST N, COWLES K, et al. CODA: convergence diagnosis and output analysis for MCMC[J]. R News, 2006, 6(1): 7-11.
[40] 官文江, 吴佳文, 曹友华. 利用后向预报方法分析印度洋黄鳍金枪鱼资源评估模型[J]. 中国海洋大学学报 (自然科学版), 2020, 50(2): 52-59. [41] KIM T K. T Test as a parametric statistic[J]. Korean J Anesthesiol, 2015, 68(6): 540-546. doi: 10.4097/kjae.2015.68.6.540
[42] RIVARD D. Effects of systematic, analytical, and sampling errors on catch estimates: a sensitivity analysis[J]. Can Spec Publ J Fish Aquat Sci, 1983, 66: 114-129.
[43] LAI H L, GALLUCCI V F. Effects of parameter variability on length-cohort analysis[J]. ICES J Mar Sci, 1988, 45(1): 82-92. doi: 10.1093/icesjms/45.1.82
[44] 李忠炉, 金显仕, 单秀娟, 等. 小黄鱼体长-体质量关系和肥满度的年际变化[J]. 中国水产科学, 2011, 18(3): 602-610. [45] 吴斌, 方春林, 贺刚, 等. FiSAT II 软件支持下的体长股分析法探讨[J]. 南方水产科学, 2013, 9(4): 94-98. [46] HOLLOWED A B, IANELLI J N, LIVINGSTON P A. Including predation mortality in stock assessments: a case study for Gulf of Alaska walleye pollock[J]. ICES J Mar Sci, 2000, 57(2): 279-293. doi: 10.1006/jmsc.1999.0637
-
期刊类型引用(1)
1. 刘尊雷，杨林林，金艳，袁兴伟，张翼，张辉，许敏，程家骅，严利平. 基于CMSY和BSM的东海区重要渔业种类资源评估. 中国水产科学. 2023(06): 735-752 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 179
- HTML全文浏览量: 99
- PDF下载量: 53
- 被引次数: 1
粤公网安备 44010502001741号
