In aquaculture systems, the accumulation of high concentration of nitrite, toxic to aquatic organisms, is commonly prevented by active removal by nitrite oxidizing bacteria(NOB)^[1-2].

In newly set-up aquaculture systems, nitrite can reach concentration toxic to fish and shrimp before a sufficient biomass of NOB established. To reduce the length of time for establishment of NOB, commercial preparations of these organisms are available to seed the aquarium environment^[3-5].

The optimization of fermentation medium is of primary importance in the development of any fermentation processes. Conventionally, fermentation process was optimized by implementing one factor at a time^[6]. Whereas at present, this approach has been replaced with statistical designs for screen of important factors and optimize of those important factors^[7-8]. The use of statistical experimental design in the optimization of fermentation processes or media is well documented^[9-10]. But there was no studies dealing with the optimization of nitrite oxidizing bacteria for improving the nitrite oxidizing rate.

In the present work, we reported a sequential optimization strategy for nitrite oxidizing rate by nitrite oxidizing bacteria. The objective of this paper is how to use statistical experimental designs to optimize the fermentation media for nitrite oxidizing rate in shake flask experiments, and to apply the nitrite oxidizing bacteria preparations to treat the nitrite of aquaculture.

1.   Materials and Methods

1.1   Organism and culture conditions

Nitrite oxidizing bacteria (NOB 013) was isolated from aquaria, and stored in the vapor phase above liquid nitrogen. Before experiment, NOB was incubated at 28~30℃ in 500 mL seed cultures containing NaCl (0.3 g · L^-1), MgSO₄ · 7H₂O (0.14 g · L^-1), FeSO₄ ·7H₂O (0.03 g · L^-1), KH₂PO₄ (0.136 g · L^-1), NaNO₂ (0.5 g · L^-1), NaHCO₃ (1.6 g · L^-1).The pH was adjusted to 7.6. The medium was placed into 1 000 mL Erlenmeyer at 170 rpm for 2 days.

1.2   Analytical method

Because of the strong adhesion of NOB^[11], it was very difficult to count the number of NOB. In this paper, the nitrite oxidizing rate of NOB served as response. The nitrite oxidizing rate was determined by incubating with NaNO₂ as substrate at 30℃ and pH 7.5~7.8^[12]. The unit is mg NO₂^--N · (g MLSS · d)^-1 (mixed liquor suspended solids, MLSS).

1.3   Experimental type and software

1.3.1   Plackett-Burman design

Plackett-Burman design is based on the first order model:

Where, Y is the response, β₀ is the model intercept and β_i is the linear coefficient, and X_i is the level of the independent variable. For screening purpose, various medium components and culture parameters were investigated. Based on the Plackett-Burman design, each factor was prepared in two levels: -1 for low level and +1 for high level. Eight assigned variables and three unassigned variables, commonly referred as the dummy, were screened in eighteen experimental designs(with three centre points). Tab. 1 illustrated the levels of each factor used in the experimental design, whereas, Tab. 2 represents the design matrix. The statistical software package Minitab (Version 15.1, Minitab Inc., Pennsylvania, USA) was used to analyze the experimental design. The purpose of three centre points was to assess the error and curvature.

Table  1.  Level of the variables and statistical analysis of Plackett-Burman design

code	variable	low level (-1)	high level (+1)	effect	t-values	P-values
X1	NaHCO3	2.0	3.0	33.33	2.29	0.070
X2	Na2CO3	0.2	0.4	150.67	10.36	0.000
X3	NaNO2	1.5	2.5	135.67	9.33	0.000
X4	Glucose	0	0.3	-56.67	-3.90	0.011
X5	FeSO4·7H2O	0.03	0.05	-7.67	-0.53	0.621
X6	NaCl	0.3	0.4	36.67	2.52	0.053
X7	KH2PO4	0.05	0.1	2.33	0.16	0.879
X8	MgSO4·7H2O	0.05	0.1	12.33	0.85	0.435

下载: 导出CSV 

| 显示表格

Table  2.  Plackett-Burman design matrix

run	X1	X2	X3	X4	X5	X6	X7	X8	nitrite oxidizing rate/mg NO2-N·(g MLSS·d)-1
1	2.5	0.3	2.0	0.15	0.04	0.35	0.075	0.075	857
2	2.0	0.2	1.5	0.00	0.03	0.30	0.050	0.050	613
3	3.0	0.2	2.5	0.00	0.03	0.30	0.100	0.100	796
4	2.0	0.2	1.5	0.30	0.05	0.40	0.050	0.100	597
5	2.5	0.3	2.0	0.15	0.04	0.35	0.075	0.075	878
6	3.0	0.4	1.5	0.30	0.05	0.30	0.100	0.050	743
7	2.0	0.4	1.5	0.00	0.03	0.40	0.100	0.100	795
8	3.0	0.4	2.5	0.00	0.05	0.40	0.050	0.100	974
9	2.0	0.4	2.5	0.30	0.03	0.40	0.100	0.050	873
10	3.0	0.2	1.5	0.00	0.05	0.40	0.100	0.050	641
11	3.0	0.4	1.5	0.30	0.03	0.30	0.050	0.100	716
12	3.0	0.2	2.5	0.30	0.03	0.40	0.050	0.050	742
13	2.5	0.3	2.0	0.15	0.04	0.35	0.075	0.075	884
14	2.0	0.4	2.5	0.00	0.05	0.30	0.050	0.050	863
15	2.0	0.2	2.5	0.30	0.05	0.30	0.100	0.100	671
16	2.5	0.3	2.0	0.15	0.04	0.35	0.075	0.075	857
17	2.0	0.2	1.5	0.00	0.03	0.30	0.050	0.050	613
18	3.0	0.2	2.5	0.00	0.03	0.30	0.100	0.100	796
Note: S=25.18;R2=98.23%

下载: 导出CSV 

| 显示表格

1.3.2   Box-Behnken design

In order to optimize the important factors for enhanced nitrite oxidizing rate, a three variable Box-Behnken design with three replicates at the center point was applied. For statistical calculations, the relation between the coded values and actual values are described as the following equation:

Where X_i is a coded value of the variable; A_i is the actual value of variable; A₀ is the actual value of the A₀ at the centre point; and △A is the step change of variable. The levels of the variables and the experimental design were shown in Tab. 3. A second-order polynomial function was fitted to correlate relationship between variable and response. The quadratic equation was following:

Table  3.  The Box-Behnken design with three independent variables

run	Na2CO3/g·L-1			NaNO2/g·L-1			NaCl/g·L-1		nitrite oxidizing rate/mg NO2-N·(gMLSS·d)-1
	X1	Code X1		X2	Code X2		X3	Code X3
1	0.35	0		2.25	0		0.35	0	901
2	0.35	0		2.50	+1		0.40	+1	874
3	0.30	-1		2.00	-1		0.35	0	817
4	0.35	0		2.00	-1		0.30	-1	846
5	0.35	0		2.25	0		0.35	0	895
6	0.30	-1		2.25	0		0.30	-1	842
7	0.35	0		2.00	-1		0.40	+1	803
8	0.40	+1		2.25	0		0.30	-1	883
9	0.30	-1		2.25	0		0.40	+1	831
10	0.35	0		2.50	+1		0.30	-1	854
11	0.40	+1		2.00	-1		0.35	0	863
12	0.40	+1		2.50	+1		0.35	0	894
13	0.35	0		2.25	0		0.35	0	896
14	0.30	-1		2.50	+1		0.35	0	875
15	0.40	+1		2.25	0		0.40	+1	835
Note: S=7.00;R2=98.17%

下载: 导出CSV 

| 显示表格

Where, Y is the predicted response; β₀ is a constant; β_i is the linear coefficients; β_ii is the squared coefficients; and β_ij is the cross-product coefficients. The statistical software package Minitab was used to analyze the experimental design.

1.4   The field trial of NOB

A field trial was conducted at Sun Yatsen city. Three separate ponds (around 0.6 hectares each) were treated with NOB microbial product, where 50 L of concentrated NOB (1.99 g VSS · L^-1) (volatile solid, VSS) with 850 mg NO₂-N · (g MLSS · d)^-1 were added to these ponds, when the nitrite was accumulated to 2.5, 2.0, 2.6 mg · L^-1 in these ponds. Three additional identically sized and stocked ponds (nitrite: 2.1, 2.6, 3.1 mg · L^-1) served as the non-treated controls, receiving the same amount of food as the treated ponds. All ponds were mechanically aerated. Water temperature and salinity in the ponds followed typical seasonal fluctuation, with an average temperature range of 27~33℃, and salinity of 23~25 mg · L^-1. Ponds were fed daily, with up to four feedings per day.

2.   Results and discussion

2.1   The screening stage: Plackett-Burman design (P-B design) and analysis

An initial set of 8 media components was identified as potentially affecting the nitrite oxidizing rate of NOB. These factors, along with their low and high factor levels, were provided in Tab. 1.

The screening design usually uses the factional factorial design(FFD), because the resolution of P-B design is III. Resolution=3 means that main effects are not confounded with other main effects, but they are confounded with one or more two-way interactions, which must be assumed to be zero for the main effects to be meaningful. However the resolution of FFD is IV, resolution= 4 means that main effects are not confounded with other main effects or two-factor interactions, and two-factor interactions can be confounded with other two-factor interaction.

But there were 8 media components in this work, running experiments would cost time and money, so P-B design was chosen to screening the important components from the all media components. The number of runs was 15(with 3 centre points) that reduced from 19 if FFD with 3 centre points was applied in this experiment. The results were provided in Tab. 2. The purpose of three centre points was to assess the error and curvature. The low and high factor levels were coded as -1 and +1, respectively, for the analysis of the data, the mid-level (for the centre points) were coded as 0.

The parameter estimates of the media components were given in Tab. 1. The media components having the significance(P-value < 0.05) at this stage including Na₂CO₃, NaNO₂, Glucose, and NaCl was an important factor(P-value=0.053).But Glucose had negative and the low level was 0 g · L^-1, so it was removed from the media. The effect of other factors was positive and had insignificant effect, fixed at low level and entered the following experiments because of reducing cost price. The most important thing is that the curvature term was significant(P=0.001 < 0.05), indicating the optimal conditions were likely inside the current experimental region.

2.2   Optimization stage: Box-Behnken design and analysis

Because the P-value of curvature was 0.001 < 0.05, which indicated the present region was optimal region, Box-Behnken design was applied to optimize three medium components. The design and result of Box-Behnken design were provided in Tab. 3.

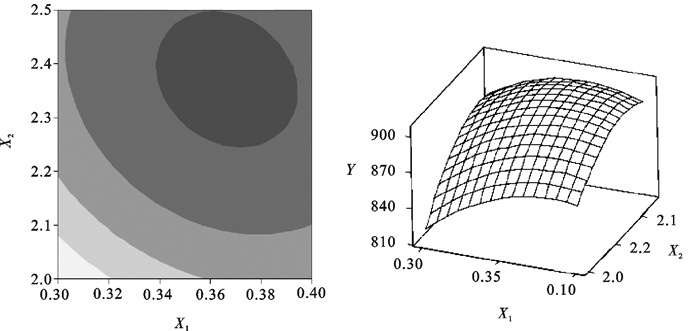
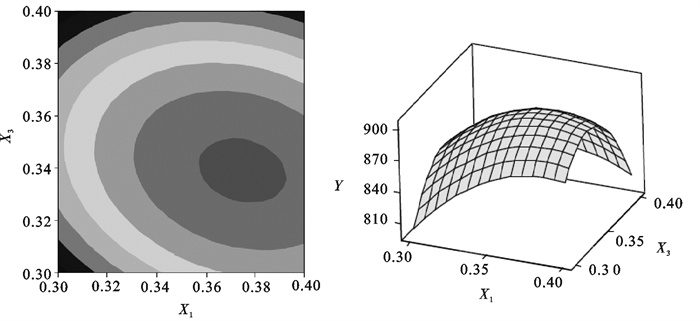
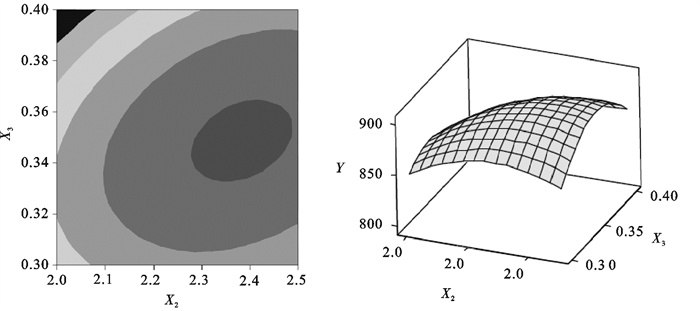
The R² was 98.17%, and the P-value of lack of fit was 0.124, that indicated the model appeared to be appropriate for the optimal region. The response surface and contours also indicated the same result(Fig. 1~3).By applying the Box-Behnken design, the following second-order polynomial equation was found to explain the nitrite oxidizing rate:

Figure  1.  The corresponding contour plot and response surface plot showing the effects of Na₂CO₃, NaNO₂ and their mutual interaction on nitrite oxidizing rate, with 0 level of NaCl(0.35 g · L^-1)

下载: 全尺寸图片 幻灯片

Figure  2.  The corresponding contour plot and response surface plot showing the effects of Na₂CO₃, NaCl and their mutual interaction on nitrite oxidizing rate, with 0 level of NaNO₂(2.25 g · L^-1)

下载: 全尺寸图片 幻灯片

Figure  3.  The corresponding contour plot and response surface plot showing the effects of NaNO₂, NaCl and their mutual interaction on nitrite oxidizing rate, with 0 level of Na₂CO₃(0.35 g · L^-1).

下载: 全尺寸图片 幻灯片

Where, Y is the predicted nitrite oxidizing rate; X₁, X₂, and X₃ are the values of Na₂CO₃, NaNO₂ and NaCl, respectively.

The parameter estimates(Tab. 4) and analysis of variance(Tab. 5) suggest that the linear, square and interaction terms have a significant effect on nitrite oxidizing rate(P-value < 0.05).

Table  4.  Parameters estimates of Box-Behnken design

term	coefficient	t-value	P-value		term	coefficient	t-value	P-value
constant	-3 194.6	-5.862	0.002		X2×X2	-308.7	-5.294	0.003
X1	7 206.7	5.558	0.003		X3×X3	-13 516.7	-9.273	0.000
X2	1 221.0	4.112	0.009		X1×X2	-540.0	-1.928	0.112
X3	7 716.7	5.952	0.002		X1×X3	-3 700.0	-2.642	0.046
X1×X1	-6 316.7	-4.333	0.007		X2×X3	1 260.0	4.498	0.006

下载: 导出CSV 

| 显示表格

Table  5.  Analysis of variance

resource	DF	Adj SS	Adj MS	F-value	P-value
regression	9	13 186.43	1 465.16	29.88	0.001
linear	3	2 954.63	984.88	20.09	0.003
square	3	5 788.68	1 929.56	39.35	0.001
interaction	3	1 516.75	505.58	10.31	0.014
residual error	5	245.17	49.03
lack-of-fit	3	224.50	74.83	7.24	0.124
pure error	2	20.67	10.33
total	14

下载: 导出CSV 

| 显示表格

From equations derived by differentiation of Eq.(4), the optimal value of X₁, X₂ and X₃ in the uncoded units were 0.37, 2.36 and 0.34 respectively. Correspondingly, we can obtain the maximum point of the model, which was 905.0 mg NO₂-N · (g MLSS ·d)^-1[2.30 g NO₂-N · (g MLSS ·d)^-1], and this nitrite oxidizing rate exceeded the results of Grommen et al. [0.3~0.5 g NO₂-N · (g MLSS · d)^-1]^[13].

Using the software, the response surface curves and its corresponding contour curves described by the regression model were constructed in Fig. 1~3. Here, each response surface plot represented the effect of two independent variables at an optimal level of the third variable. The shape of the corresponding contour plots indicated whether the mutual interactions between the independent variables were significant or not. As shown in Fig. 1~3, the response surface of nitrite oxidizing rate showed a clear peak, indicating that the optimum condition fell inside the design boundary well.

2.3   The field trial of NOB

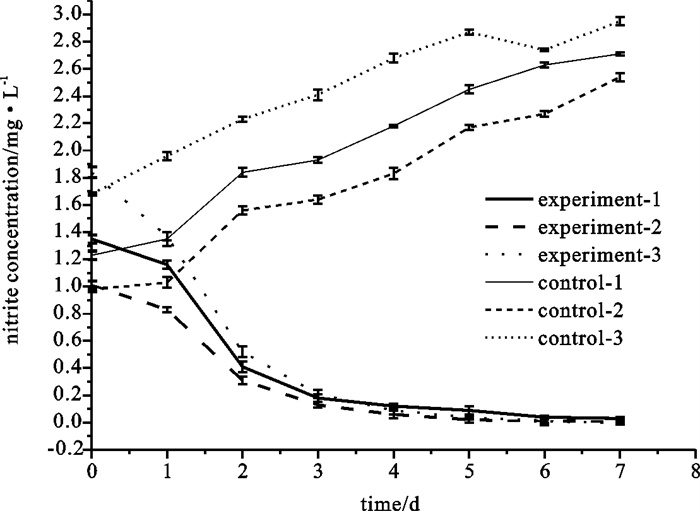
The results showed clearly that the NOB was effective at oxidizing nitrite to nitrate(Fig. 4). The nitrite concentrate was reduced to 0.1 mg · L^-1 after 3 days. However, the nitrite concentrate of no-treated controls accumulated to 2.7, 3.2 and 3.8 mg · L^-1 after 3 days.

Figure  4.  Variation of nitrite concentration in shrimp aquaculture water as a function of time (2006.7.8~2006.7.15)

下载: 全尺寸图片 幻灯片

3.   Conclusions

(1) Estimated optimum medium composition of the nitrite oxidizing rate was as follows: NaHCO₃, 2.0 g · L^-1; NaNO₂, 2.36 g · L^-1; Na₂CO₃, 0.37 g ·L^-1; NaCl, 0.34 g · L^-1; KH₂PO₄, 0.05 g · L^-1; MgSO₄ · 7H₂O, 0.05 g · L^-1; and FeSO₄ · 7H₂O, 0.03 g ·L^-1. The nitrite oxidizing rate reached a maximum at 905.0 mg NO₂-N · (g MLSS · d)^-1.

(2) The proper use of sequential statistical experimental design can allow the experimentalist to reduce the complexity of a problem by identifying the important effect factors and focusing future experiments on those factors.

(3) The results of the field trial showed that appropriate amount of NOB microbial product can reduce the nitrite to safe level(< 0.2 mg · L^-1) quickly after 3 days.