Study on selectivity of different mesh size gillnet for Nemipterus virgatus in South China Sea
-
摘要:
金线鱼刺网是南海区的主要渔具之一。根据近年来世界上刺网选择性研究常用的最大似然法原理,应用Normal、Gamma和Lognormal 3种常用的刺网选择性曲线模型,对1992年在南海区进行的45、50、55和60 mm网目尺寸金线鱼刺网捕鱼比较试验的渔获资料作了分析。结果表明,南海区金线鱼刺网的选择性最适合用Lognormal模型曲线公式描述。
Abstract:Nemipterus virgatus gillnet is one of the main fishing gears in South China Sea. According to the theory of maximum likelihood method of gillnet selectivity that rose in resent years, this paper uses the Normal, Gamma and Lognormal selectivity models, which are commonly used to describe gillnet selectivity curve, to analyze the catch data of Nemipterus virgatus from simultaneous fishing with 45, 50, 55 and 60 mm mesh sizes of gillnets in 1992. The results show that Lognormal model equation provide an adequate description for the selectivity curves of Nemipterus virgatus gillnet in South China Sea.
-
金线鱼刺网俗称红三刺网、三指刺网,是一种以金线鱼为主要捕捞对象的漂流单层刺网,兼捕大眼鲷、带鱼、刺鲳、二长棘鲷、蛇鲻、石首鱼科等。金线鱼刺网是南海区的主要传统渔具之一。据调查,1983年全区网片数已达27万多片,占刺网总数的23%①。上世纪90年代后期,由于金线鱼延绳钓和马鲛流刺网渔业的兴起,其地位有所下降,但目前仍是南海区的主要渔具之一。因此有必要开展金线鱼刺网选择性研究,为制订金线鱼刺网最小网目尺寸标准,调查和合理开发金线鱼刺网渔业资源提供科学依据。
① 傅尚郁,陈永青,魏振明,等. 南海区海洋渔具对渔业资源影响的研究, 2003.34-46.
刺网选择性研究的理论很多。目前我国学者使用较多的有Baranov(1948)方法[1]和Holt(1963)方法[2],前者利用渔获物的体长频率分布作为选择性曲线的近似分布,未考虑捕捞对象的体长分布对渔获物体长分布产生的影响;而后者是利用对比试验中2个相近网目刺网的渔获差异来估算选择性曲线,但一直受到曲线模型拟合优度检验的困扰[3]。近10年来,随着数理统计模型方法在渔具选择性研究中的应用,出现了以Hovgård (1996,1999)[4, 5],Helser (1998)[6],Millar(1997,1999)[7, 8]为代表的3种刺网选择性研究的新方法。这3种方法具有相同的内在结构,其特点是将鱼类的渔获过程用某个概率分布模型来表示, 然后根据试验渔获的总概率的最大化或试验渔获观察值与期望值差异的最小化,用最大似然法或最小二乘法原理来推算选择性曲线的参数,从而避免了绝对渔获数量对参数推算的影响。本文根据1992年在南海区进行的金线鱼刺网捕鱼比较试验数据,应用最大似然法原理,估算金线鱼刺网的选择性曲线。
1. 材料和方法
1.1 资料来源
资料来自南海水产研究所1992年7~ 9月进行的金线鱼刺网选择性试验5个航次的原始记录。试验刺网是参照广东沿海普遍采用的刺网结构定制,45、50、55和60 mm 4种网目尺寸单片刺网各5片,网衣材料为PA单丝(6磅),双死结编织,横目使用,10目误差在±3 mm之内。这4种网片除网目尺寸不同外,其他数据均相同。试验时将4种规格网片互相交错连结成一列刺网,在台山沙堤至珠海30~ 60 m水深海域作业。
5航次共捕获金线鱼1 463尾,其中45 mm网目404尾,50 mm网目388尾,55 mm网目358尾,60 mm网目313尾。每网次对所捕获的金线鱼进行生物学测定,包括体重、叉长、最大体周和鳃后缘体周等。以5 mm间隔为一叉长组,并取其中值,然后按网目尺寸统计各叉长组的渔获尾数(表 1)。
表 1 45、50、55和60 mm刺网的金线鱼渔获组成Table 1 The catch composition of Nemipterus virgatus for mesh sizes 45, 50, 55 and 60 mm gillnet叉长/mm fork length 网目尺寸 mesh size 45 mm 50 mm 55 mm 60 mm 120 1 0 0 0 125 47 1 0 0 130 28 0 0 0 135 74 1 0 0 140 75 7 0 0 145 70 26 3 0 150 66 133 3 0 155 21 100 44 2 160 14 93 97 1 165 2 5 142 48 170 4 7 48 123 175 2 11 10 68 180 0 2 4 22 185 0 1 1 21 190 0 0 1 13 195 0 1 2 4 200 0 0 1 6 205 0 0 2 3 210 0 0 0 2 合计 total 404 388 358 313 1.2 研究方法
1.2.1 选择曲线模型的估算[9]
进行海上同步试验的4种刺网除网目尺寸不同外,其它数据均相同,所以4种网片的捕捞努力量相同,另外忽略不同目大刺网的捕捞能力的差异,并且假定渔获之间相互无干扰,则网目尺寸为m的刺网捕获叉长l的金线鱼尾数Clm(即观测值)可表示为:
$$ C_{l m}=N_l S_{l m}+\varepsilon_{l m}\quad\ldots \ldots \ldots \ldots $$ (1) 式中,Nl表示遭遇网具的叉长l的金线鱼尾数;Slm表示网目尺寸为m的刺网对叉长l的金线鱼的选择率;εlm为随机误差,用以表示海况差异、鱼类行为差异等种种随机因素的影响。在概率分布模型中,通常假定εlm~N(0,б2),即Clm服从期望值为NlSlm、方差为б2的正态分布。由于Poisson分布的期望值与方差相等,为简化计算,这里设Clm服从参数为λ=NlSlm的Poisson分布。实际上,由于鱼类的集群分布,其渔获过程近似于负二项分布,但如采用负二项分布模型其计算非常复杂,因此在目前的渔业文献中,通常用正态分布或Poisson分布来描述渔获过程。Millar and Holst(1997)的经验也证明,尽管在实践中常有方差远超过均值的过度分散问题(overdispersion),Poisson分布基本提供了一个足够的描述[7]。
由Clm服从参数为λ=NlSlm的Poisson分布,可知试验中出现观测值Clm的概率Plm为:
$$ P_{l m}=\frac{\lambda^{C_{l m}}}{C_{l m}!} e^{-\lambda}\quad\ldots \ldots \ldots \ldots $$ (2) 则试验渔获的总概率P为:
$$ P=\prod\limits_{l m} \frac{\lambda^{C_{l m}}}{C_{l m}!} e^{-\lambda}\quad\ldots \ldots \ldots \ldots $$ (3) 根据最大似然法原理:未知参数的最适估计值是使Clm出现的“概率”达到最大的值。因此所求的最适选择曲线Slm应是使P值达到最大的曲线[10]。
因为lnP为P的单调函数,lnP和P在同一处达到最大值,对(3)式进行对数等价变换,并将λ=NlSlm代入得:
$$ \begin{array}{r} \ln P=\sum\limits_l \sum\limits_m\left[C_{l m} \ln \left(N_l S_{l m}\right)-\ln \left(C_{l m}!\right)\right. \\ \left.-N_l S_{l m}\right]=\max \quad \ldots \ldots \ldots \ldots . \end{array} $$ (4) lnP在最大值时,求Nl的偏导数可推出:
$$ N_l=\sum\limits_m \mathrm{C}_{l m} / \sum\limits_m \mathrm{~S}_{l m} \quad \ldots \ldots \ldots \ldots $$ (5) 将(5)代入(4)可得:
$$ \begin{array}{r} \ln P=\sum\limits_l \sum\limits_m\left[C_{l m} \ln \left(\frac{\sum\limits_m C_{l m}}{\sum\limits_m S_{l m}} S_{l m}\right)\right. \\ \left.-\ln \left(C_{l m}!\right)-\frac{\sum\limits_m C_{l m}}{\sum\limits_m S_{l m}} S_{l m}\right]=\max \quad \cdots \cdots\cdots\cdots \end{array} $$ (6) 刺网选择性曲线一般呈钟形,常用Normal模型、Gamma模型和Lognormal模型来作近似描述,分别将这3种模型代入(6)式,并利用MS-EXCEL软件的规划求解(SOLVER add-in)工具,求解ln P最大时的模型参数,即可估算出金线鱼刺网选择曲线模型Slm(表 2)。
表 2 刺网选择曲线模型Table 2 Models of selectivity curve of gillnet模型 model 选择曲线 selectivity curve 参数 parameters Normal $S_{l m}=\exp \left[\frac{-\left(l-k_l m\right)^2}{2 k_2 m^2}\right]$ (k1, k2) Gamma $S_{l m}\left[\frac{l}{(\alpha-1) k m}\right]^{\alpha-1} \exp \left(\alpha-1-\frac{l}{k m}\right)$ (α, k) Lognormal $S_{l m}=\exp \left[-\left(\ln \frac{1}{\mathtt{m}}-\mathtt{μ}\right)^2 / 2\mathtt{б}^2\right]$ (μ, б) 1.2.2 拟合优度检验
对于求出的3种选择曲线模型,需进一步分析三者中哪个最适合描述金线鱼刺网选择性曲线,并检验该模型的拟合优度,即检验实际的观测值与模型估算的理论值之间的吻合程度,以确定求得的模型是否有实际意义。
Pearson卡方(即χ2检验)最常用来检验此类模型的拟合优度。但使用Pearson卡方需要满足“不能有单元格的期望值< 1”和“不能有20%以上单元格的期望值< 5”这2个条件,否则会对检验结果造成较大干扰[11]。本例中的期望值NlSlm明显不能满足这2个条件,所以这里采用似然比卡方(Likelihood Ratio)来检验模型的拟合优度,其检验统计量为:
$$ G=2 \sum\limits_i \sum\limits_m C_{l m} \ln \left(\frac{C_{l m}}{N_l S_{l m}}\right) \quad \ldots \ldots \ldots \ldots $$ (7) 式中,G——检验样本分布偏离理论分布的严重程度,其分布近似于χ2分布;G/df——检验样本分布与理论分布的相似程度,df表示自由度。
G/df的理论期望值为1,越接近1,说明模型的拟合度越好;G/df < 5时,可以认为模型的拟合优度比较好。需要明确的是:到底G/df多大时模型才算通过拟合优度检验并无绝对标准,要根据具体情况而定,因为拟合优度并不是决定模型取舍的唯一标准,有时为了使模型有较合理的解释,可能会在某种程度上牺牲拟合优度,也就是说模型的合理解释才是第一位的[12]。
2. 结果与讨论
2.1 3种模型参数估算值
根据上述的方法及数据,估算出南海区金线鱼刺网的Normal、Gamma和Lognormal模型参数如表 3所示。
表 3 金线鱼刺网选择曲线模型的估算Table 3 The estimation of selectivity curves of gillnet for Nemipterus virgatus模型 model 参数 parameters G df G/df Normal (k1,k2)= (3.0 663,0.0 389) 522.36 55 9.5 Gamma (α,k)=(247.4 036,0.0 124) 481.18 55 8.7 Lognormal (μ,б)=(1.1 148,0.0 633) 463.13 55 8.4 由表 3可见,在Normal、Gamma和Lognormal模型中,Lognormal模型的G值最小,即Lognormal模型的样本分布偏离理论分布的程度最小。因此在这3个模型中,以Lognormal模型最适合描述金线鱼刺网的选择曲线,其表达式如下:
$$ \begin{aligned} S_{l m}= & \exp \left[-\left(\ln \frac{l}{m}-1.1148\right)^2 / 2\right. \\ & \left.\times 0.0633^2\right] \cdots \cdots \cdots\cdots \end{aligned} $$ (8) 从表 3还可看到,Lognormal模型的G/df值为8.4,大于5,说明模型的拟合优度并不太理想。
2.2 模型合理性探讨
模型拟合不佳的可能原因有:建立的模型本身有定型错误;用来拟合模型的数据包含一个或多个异常值。虽然进行海上试验时存在多种非可控因素的影响,出现异常值是难以避免的,但分析Lognormal模型的合理性是必要的。
统计模型通常采用残差分析法[7]来探讨其合理性。本文通过分析南海区45、50、55和60 mm刺网的最大渔获对应叉长及估算出的最大选择叉长之间的关系来探讨模型的合理性(表 4)。虽然只有当刺网的选择范围远小于捕捞对象的体长分布范围时,渔获物的体长分布才近似于选择曲线,但二者无疑有着某种程度的联系。
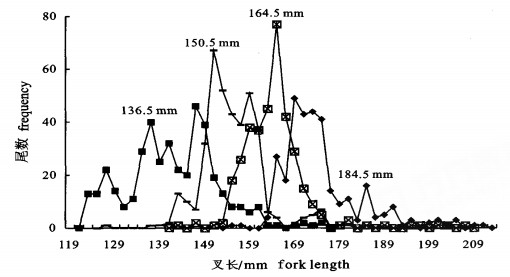
表 4 金线鱼刺网的最大选择叉长和最大渔获叉长Table 4 Fork length of largest selectivity and largest catches of gillnet for Nemipterus virgatus网目尺寸 mesh size 45 mm 50 mm 55 mm 60 mm 最大选择叉长/mm fork length of largest selectivity 137.1 152.4 167.6 182.9 最大渔获叉长/mm fork length of largest catches 146.5 150.5 164.5 168.5 首先利用公式(8)求出选择率Slm为100%时,4种网目尺寸刺网对应的最大选择叉长,然后再将捕获的金线鱼按叉长2 mm间隔分组,并绘出叉长分布图(图 1)。
从表 4和图 1可知:50和55 mm刺网的最大渔获对应叉长分别为150.5、164.5 mm,基本与50和55 mm刺网的最大选择叉长152.4、167.6 mm相吻合;45 mm刺网的最大渔获叉长虽然为146.5 mm,但其图形有个非常明显的次峰值,对应叉长136.5 mm,恰好和45 mm刺网的最大选择叉长137.1 mm相吻合;60 mm刺网的最大选择叉长为182.9 mm,而在图上也有个叉长为184.5 mm的小峰值与之对应。可得出结论:估算的金线鱼刺网的Lognormal模型是符合实际的。
45 mm刺网的最大渔获之所以出现在146.5mm叉长组,是因为试验海区146.5 mm叉长组的金线鱼资源量要多于136.5 mm叉长组的金线鱼资源量;60 mm刺网的情况同样可作如是解释,其最大选择叉长和最大渔获叉长分别为182.9和168.5 mm,二者差别较大,这从另一个角度说明如用渔获物的体长分布作为选择性曲线的近似分布,而不考虑捕捞对象资源量分布的影响,估算出的选择曲线和实际情况可能会有较大的出入。
2.3 选择曲线
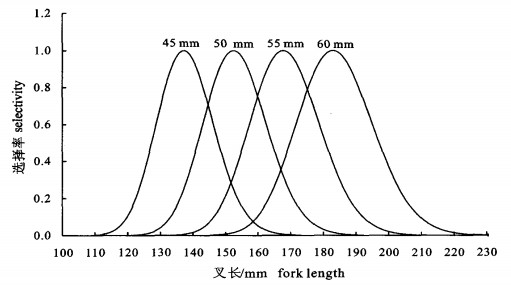
在合理范围内,利用公式(8)可方便求出任一网目尺寸金线鱼刺网的选择性曲线,也可求出任一叉长金线鱼的最适捕捞网目尺寸。现估算并绘出网目尺寸为45、50、55和60 mm金线鱼刺网的Lognormal选择曲线如图 2所示。从图 2可见,4种网目尺寸刺网的选择曲线形状完全相同,只是位置有所变化。
2.4 金线鱼资源分布估算
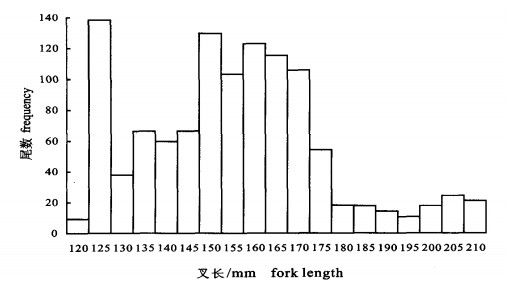
金线鱼刺网Lognormal选择曲线Slm确定后,由公式(5),可同时估算出试验时与每种网目刺网遭遇的叉长l的金线鱼尾数Nl,结果如图 3所示。
知道遭遇网具的捕捞对象的数量及体长分布估算值,再结合作业时间、捕捞对象的游速等影响因素,就可以对试验海区捕捞对象的资源量及资源结构进行估算。
-
表 1 45、50、55和60 mm刺网的金线鱼渔获组成
Table 1 The catch composition of Nemipterus virgatus for mesh sizes 45, 50, 55 and 60 mm gillnet
叉长/mm fork length 网目尺寸 mesh size 45 mm 50 mm 55 mm 60 mm 120 1 0 0 0 125 47 1 0 0 130 28 0 0 0 135 74 1 0 0 140 75 7 0 0 145 70 26 3 0 150 66 133 3 0 155 21 100 44 2 160 14 93 97 1 165 2 5 142 48 170 4 7 48 123 175 2 11 10 68 180 0 2 4 22 185 0 1 1 21 190 0 0 1 13 195 0 1 2 4 200 0 0 1 6 205 0 0 2 3 210 0 0 0 2 合计 total 404 388 358 313 表 2 刺网选择曲线模型
Table 2 Models of selectivity curve of gillnet
模型 model 选择曲线 selectivity curve 参数 parameters Normal $S_{l m}=\exp \left[\frac{-\left(l-k_l m\right)^2}{2 k_2 m^2}\right]$ (k1, k2) Gamma $S_{l m}\left[\frac{l}{(\alpha-1) k m}\right]^{\alpha-1} \exp \left(\alpha-1-\frac{l}{k m}\right)$ (α, k) Lognormal $S_{l m}=\exp \left[-\left(\ln \frac{1}{\mathtt{m}}-\mathtt{μ}\right)^2 / 2\mathtt{б}^2\right]$ (μ, б) 表 3 金线鱼刺网选择曲线模型的估算
Table 3 The estimation of selectivity curves of gillnet for Nemipterus virgatus
模型 model 参数 parameters G df G/df Normal (k1,k2)= (3.0 663,0.0 389) 522.36 55 9.5 Gamma (α,k)=(247.4 036,0.0 124) 481.18 55 8.7 Lognormal (μ,б)=(1.1 148,0.0 633) 463.13 55 8.4 表 4 金线鱼刺网的最大选择叉长和最大渔获叉长
Table 4 Fork length of largest selectivity and largest catches of gillnet for Nemipterus virgatus
网目尺寸 mesh size 45 mm 50 mm 55 mm 60 mm 最大选择叉长/mm fork length of largest selectivity 137.1 152.4 167.6 182.9 最大渔获叉长/mm fork length of largest catches 146.5 150.5 164.5 168.5 -
[1] Baranov F I. Theory and assessment of fishing gear[M]. Chapter 7 in Theory of fishing with gillnets, 2nd ed. (Translation from Russian by Ontario Department of Lands and Forests, Maple, Ontario), 1948.
[2] Holt S J. A method for determining gear selectivity and its application[J]. ICNAF Spec Publ, 1963, 5: 106-115. https://cir.nii.ac.jp/crid/1572261549599535232
[3] Millar R B. The functional form of hook and gillnet selection curves cannot be determined from comparative catch data alone[J]. Can J Fish Aquat Sci, 1995, 52(5): 883-891. doi: 10.1139/f95-088
[4] Hovgård H. A two-step approach to estimating selectivity and fishing power of research gillnets used in Greenland waters[J]. Can J Fish Aquat Sci, 1996, 53(5): 1007-1013. doi: 10.1139/f96-022
[5] Hovgård H, Lassen H, Madsen N, et al. Gillnet selectivity for North Sea cod Gadus morhua): Model ambiguity and data quality are related[J]. Can J Fish Aquat Sci, 1999, 56(7): 1307-1316. doi: 10.1139/f99-070
[6] Helser T E, Geaghan J P, Condrey R E. Estimating gillnet selectivity using nonlinear response surface regression[J]. Can J Fish Aquat Sci, 1998, 55(6): 1328-1337. doi: 10.1139/f98-036
[7] Millar R B, Holst R. Estimation of gillnet and hook selectivity using log-linear models[J]. ICES J Mar Sci, 1997, 54(3): 471-477. doi: 10.1006/jmsc.1996.0196
[8] Millar R B, Fryer R J. Estimating size-selection curves of trawls, traps, gillnets, and hooks[J]. Rev Fish Biol Fish, 1999, 9(1): 89-116. doi: 10.1023/A:1008838220001
[9] Hovgård H, Lassen, Manual on estimation of selectivity for gillnet and longline gears in abundance surveys: 2000[R]. FAO FISHERIES TECHNICAL PAPER, 2000, 397: 32-38, 81-82.
[10] 关则良. 水产统计学[M]. 成都: 成都科技大学出版社, 1993.87-91. [11] 张文彤. SPSS11统计分析教程基础篇[M]. 北京: 北京希望电子出版社, 2002.262. https://baike.baidu.com/item/SPSS11%E7%BB%9F%E8%AE%A1%E5%88%86%E6%9E%90%E6%95%99%E7%A8%8B%EF%BC%9A%E5%9F%BA%E7%A1%80%E7%AF%87/16300662 [12] Sokal Rohll. 生物统计学导论. 萧如英译[M]. 台北: 五南图书出版公司, 1981.384-406.



 下载:
下载:
 粤公网安备 44010502001741号
粤公网安备 44010502001741号
