Fishing ground forecasting model of Ommastrephes bartramii based on support vector machine(SVM) in the Northwest Pacific
-
摘要:
柔鱼(Ommastrephes bartramii)是中国在西北太平洋主要的鱿钓捕捞对象。准确预报柔鱼渔场，对减少寻鱼时间、节省油料和提高渔获产量均有积极的意义。该研究将2002年~2012年中国在西北太平洋鱿钓产量数据、渔场时空数据以及海表温度、叶绿素a浓度、表温梯度强度和叶绿素梯度强度等海洋环境因子作为训练数据，基于支持向量机(support vector machine, SVM)的方法，建立了以月为时间分辨率、0.5°×0.5°为空间分辨率的西北太平洋柔鱼渔场的预报模型。该模型以径向基函数(RBF)为核函数，利用10折交叉验证和网格选优法，确定了最优惩罚项因子和核函数参数值的组合(C，γ)，分别为1.41和2.83，样本分类精度达73.6%。利用2013年7月~11月环境数据，对模型进行了精度检验，预报准确率为53.4%~60.0%，平均准确率为57.4%。研究认为，在训练数据不够充分的条件下，SVM模型可成为西北太平洋柔鱼渔场预报的一个有效手段。
Abstract:Ommastrephes bartramii is one of the most important commercial fishing targets for China in the Northwest Pacific. Accurate forecast of the fishing ground helps locate the shoal, save fuel and improve yield. In the present study, historical catch log data and environmental factors including sea surface temperature (SST), chlorophyll-a concentration(Chl), SST gradient(SSTG) and Chl gradient(ChlG) in the Northwest Pacific Ocean were collected. Based on the support vector machine (SVM), squid fishing ground forecast model was established with Radial Basis Function (RBF) kernel in the monthly resolution and the spatial resolution of 0.5°×0.5°. The optimal combination of penalty parameter (C=1.41) and kernel parameter (γ=2.83) were obtained by 10-fold cross validation and grid-search when the accuracy of model reached 73.6%. A simulated accountancy test was carried out using monthly environmental data in 2013. The accuracy rate ranged from 53.4% to 60.0% with 57.4% on average. The result suggests that SVM can provide an efficient means for squid fishing ground forecast with a small training dataset in the Northwest Pacific.
-
西北太平洋柔鱼(Ommastrephes bartramii)属于大洋性、季节性南北洄游的头足类，通常分为4个种群，即中部秋生群、东部秋生群、西部冬春生群和中东部冬春生群[1-2]，其中170°E以西为柔鱼的冬春生群，是中国鱿钓船在该海域的传统捕捞对象[3]。自20世纪90年代以来，中国在该海域的鱿钓生产规模呈逐步扩大趋势，近年渔船数量达150~250艘，2001年~2008年柔鱼年渔获量稳定在(8~11)×104 t之间[4-5]，在中国远洋渔业中占有重要地位。但该海域分布着黑潮与亲潮两大流系，海况情况复杂，增加了确定渔场的难度和寻渔成本。准确快速地对该海域的柔鱼渔场进行预报，不仅可以为渔业企业合理安排渔业生产提供有益的参考，而且可以在减少寻渔时间的基础上达到提高渔获产量的目的。
鉴于柔鱼类易受环境变化影响的特点，国内外学者构建了多种模型用来分析渔业资源、渔场与环境因子的关系，或将各种模型应用到渔场预报当中，包括地统计学插值、贝叶斯和模糊逻辑方法、广义加性模型(GAM)、栖息地指数(HSI)模型、随机森林以及分类决策树等，其中预报模型的预报准确率为50%~75% [6-14]。然而在实际构建渔场预报模型时，大多需要大量或者完备的数据集才能达到比较理想的预报性能，但这一条件很难满足。因为迄今为止，有利用价值的渔获数据与可以获取的大面积遥感环境数据的时间序列长度均有限。而支持向量机(support vector machine，SVM)是一种以统计学习理论为基础的机器学习算法，该法减低了对数据分布的要求，在训练样本不足的情况下仍可得到理想的分类效果。由于SVM是一个凸问题，这就决定了它不会落入局部最优解的陷阱。SVM在渔业方面也有所应用，如袁春红等[15]基于SVM模型，利用北太平洋柔鱼产卵场的海表温度(sea surface temperature，SST)和单位捕捞努力量渔获量(catch per unit effort，CPUE)数据，对该海域的资源丰度进行了中长期评估。汤鸿益[16]在先验知识的基础上设计了阿根廷滑柔鱼(Illex argentinus)罗德尼渔场渔情的SVM预报模型，与神经网络模型比较结果表明，SVM模型的性能更为优越。但上述研究或将重点放在柔鱼的年间资源丰度的评价上，不能作为短期预报应用；或所选环境因子不能满足实际渔场预报即时性的需要，因此很难达到实际渔场预报的要求。另外上述研究在SVM参数选择上采用了人为指定的方法，较难从客观上得到一个最优的预报模型。
该研究以短期渔场预报为出发点，将西北太平洋历史鱿钓产量数据、渔场时空和多个海洋环境因子信息作为训练数据，基于支持向量机的方法，以径向基函数(RBF)为核函数，利用交叉验证和网格选优的方法，确定模型的最优参数，从而消除了人为指定参数带来的主观影响，使建立短期柔鱼渔场的预报模型更为合理。通过该研究，以期为大洋性渔场预报模型的建立提供一定的参考。
1. 材料与方法
1.1 数据的获取与处理
1.1.1 渔获数据
该研究的柔鱼渔获数据来自上海海洋大学鱿钓技术组，其内容涵盖的时间跨度为2002年~2013年，其中7月~11月为捕捞的主要时期，作业的经、纬度范围分别为145°E~170°E、35°N~50°N，渔获信息内容包括捕捞日期、空间坐标位置(经度和纬度)、渔获产量以及作业次数等。每艘渔船一般将一年作为一个航次，分天统计当天的捕捞产量，数据集总的记录数达55 968条。在构建模型之前，先将渔获信息以月为时间单位、0.5°×0.5°网格为空间单位汇总，再根据TIAN等[17]提供的方法计算出每个月份各个渔区网格的CPUE，其公式可表示为：
$$ \mathrm{CPUE}=\frac{\sum Catch }{\sum Fishingdays } $$ (1) 其中∑Catch为0.5°×0.5°网格中1个月的总产量，∑Fishingdays为该网格当月总的船天数，CPUE的单位为t · (船· d)-1。为了适应分类模型的需要，将渔区网格依据CPUE的大小分为两类。有研究表明，三分位数可将样本在统计基础上进行分级，是对连续数据进行离散化的一种常用方法[18]，在过去包括柔鱼在内的渔场预报模型的研究中也有所应用[19]，因此该研究借鉴上述经验，将各个月份的渔区以CPUE三分位点的高值点(66.7%)作为分割点，将渔区分为低CPUE和高CPUE两类，分别用逻辑值“非”和“是”表示。
1.1.2 海洋环境数据
大量研究表明，柔鱼受包括海表温度、叶绿素a浓度、垂直和表层温度及叶绿素锋面、海面高度异常等多种因素的影响，可作为分析柔鱼渔场分布和资源变动的重要解释因子[7, 11-12, 20]。应用遥感手段，可以大面积获取多种海洋环境要素信息[21]。鉴于上述原因，同时为了满足实际渔场预报的需要，该研究选取了即时性较强、获取方便的环境遥感数据作为解释因子，其中包括SST、表层叶绿素a浓度(Chl)、SST梯度强度(SSTG)、Chl梯度强度(ChlG)。前两者均来自http://oceancolor.gsfc.nasa.gov/网站的MODIS月平均的三级环境信息产品。为了使环境数据与生产数据匹配，在此也将海表温度与叶绿素a浓度数据按不同年份以月为时间单位，以0.5°×0.5°为空间分辨率进行平均化处理。
在此基础上，应用求梯度幅值(gradient magnitude，GM)的方法来计算SST梯度强度[22]。设与当前渔区相邻的上下左右4个网格点的海表温度为SSTi±1, j和SSTi, j±1，则差分格式的SST梯度强度(℃ · km-1)可表示为：
$$ S S T G_{i, j}=\sqrt{\left[\left(S S T_{i+1, j}-S S T_{i-1, j}\right) / \Delta y\right]^2+\left[\left(S S T_{i, j+1}-S S T_{i, j-1}\right) / \Delta x\right]^2} $$ (2) 其中i、j分别为当前渔区格点的行和列的索引号，△y表示i-1行和i+1行间的距离，Δx表示j-1列和j+1列间的距离，单位均为km。
同理，可计算得到叶绿素a浓度的梯度强度(mg · m-3 · km-1)为：
$$ ChlG_{i, j}=\sqrt{\left[\left(C h l_{i+1, j}-C h l_{i-1, j}\right) / \Delta y\right]^2+\left[\left(C h l_{i, j+1}-C h l_{i, j-1}\right) / \Delta x\right]^2} $$ (3) 1.1.3 解释变量的预处理
由于当解释变量(包括时空因子和环境因子)的平均值为0且方差相同时，可使模型有较快的收敛速度[23]，因此首先将不同解释变量进行规范化处理：计算所有输入变量的平均值作为输入变量的中心值，标准差作为变化的幅度。得到训练数据集中各个变量对应的变换参数见表 1。
表 1 解释变量的规范化参数Table 1. Parameters of explanatory variables for normalization月份
month经度/°
longitude纬度/°
latitude海表温度
SST叶绿素a浓度
ChlSST梯度强度
intensity of SST gradientChl梯度强度
intensity of Chl gradient中心值center 9.066 9 155.516 1 42.226 8 16.167 4 0.427 6 0.019 8 0.002 2 变化幅度scale 1.308 6 4.456 4 1.582 4 3.190 0 0.279 1 0.012 0 0.002 5 1.2 模型原理
1.2.1 SVM [24]
SVM是一种以统计学习理论为基础的机器学习算法，其最大的特点是在结构风险最小化原则的基础上，使其泛化能力达到最大化。设有一组带标签的训练集(Xi, yj)，其中i=1, 2, ...N, Xi为m维向量，包括渔场的时空属性(月份、经度和纬度)及环境属性(SST、Chl、SST梯度强度和Chl梯度强度)，yi为分类标签，即渔场为“是”和“非”，分别用1与-1表示。SVM就是对以下最优问题进行求解：
$$ \min\limits_{w, b, \xi} \frac{1}{2} W^T W+C \sum\limits_{i=1}^N \xi $$ (4) 满足
$$ y_i\left(W^T \phi\left(x_i\right)+b\right) \geqslant 1-\xi_i $$ (5) 其中C是一个大于0的数，称为误差项的惩罚因子，ξ称为松弛变量。在SVM中，利用函数ϕ将用于训练的m维向量Xi映射到一个更高的维空间，并在此高维空间中找到一个最大间隔。为了使低维的向量X向高维空间映射，需定义一个核函数：
$$ K\left(x_i, x_j\right)=\left\langle\phi\left(x_i\right), \phi\left(x_j\right)\right\rangle $$ (6) 其中＜·＞表示2个向量的点乘。其最优的判别函数为：
$$ f(x)=\operatorname{sgn}\left[\sum\limits_{i=1}^\iota y_i a_i \cdot K\left(x, x_i\right)+b\right] $$ (7) 其中sgn为符号函数，取值为1或-1；ι为支持向量的个数，xi为训练后得到的第i个支持向量，x为输入的属性向量，K(xi, xj)为核函数。由于RBF更适合处理类别标记与属性之间为非线性关系的情况[25]，因此模型选用该函数作为核函数，其定义为：
$$ K\left(x_i, x_j\right)=\mathrm{e}^{-\gamma\left\|x_i-x_j\right\|^2} $$ (8) 其中γ是核函数的参数，同惩罚因子C一样，需在训练时通过交叉验证得到最佳值。
1.2.2 最优参数的确定方法
如1.2.1所述，在含有径向基函数的SVM模型中，有(C，γ)2个参数有待确定，解决该问题的方法之一就是v-折交叉验证[25]。具体方法为：将所有数据集随机分为v个子数据集，使用其中v-1个子数据集作为训练数据，确定一个参数对(C，γ)，经学习后得到一个SVM分类器。将剩下的一个子数据集为验证数据，将其代入分类器中，计算模型的预报准确率。然后以指数增长的方式不断改变(C，γ)的值，重新训练得到新的模型，再次检验模型的预报精度，最终可获取能使模型精度达到最高的参数对(C，γ)。该方法称为网格选优法(grid-search)。
1.2.3 渔场预报精度的检验方法
渔场预报精度可以用来衡量预报渔场与实际渔场的符合程度。文献[19]和[26]提供了一种定量检验渔场预报精度的方法，其综合预报准确率p可定义为：
$$ p=\left(\frac{\left|C_1 \cap C_1{ }^{\prime}\right|}{\left|C_1\right|}+\frac{\left|C_0 \cap C_0{ }^{\prime}\right|}{\left|C_0\right|}\right) / 2 \times 100 \% $$ (9) 其中C1为研究海域中实际渔场为“是”的渔区集合，C0为该海域实际生产中的“非”渔场渔区的集合，C1′为通过模型预报得到的渔场为“是”的渔区的集合，C0′是预报得到的“非”渔场渔区的集合。
2. 结果
2.1 渔场预报模型的训练结果
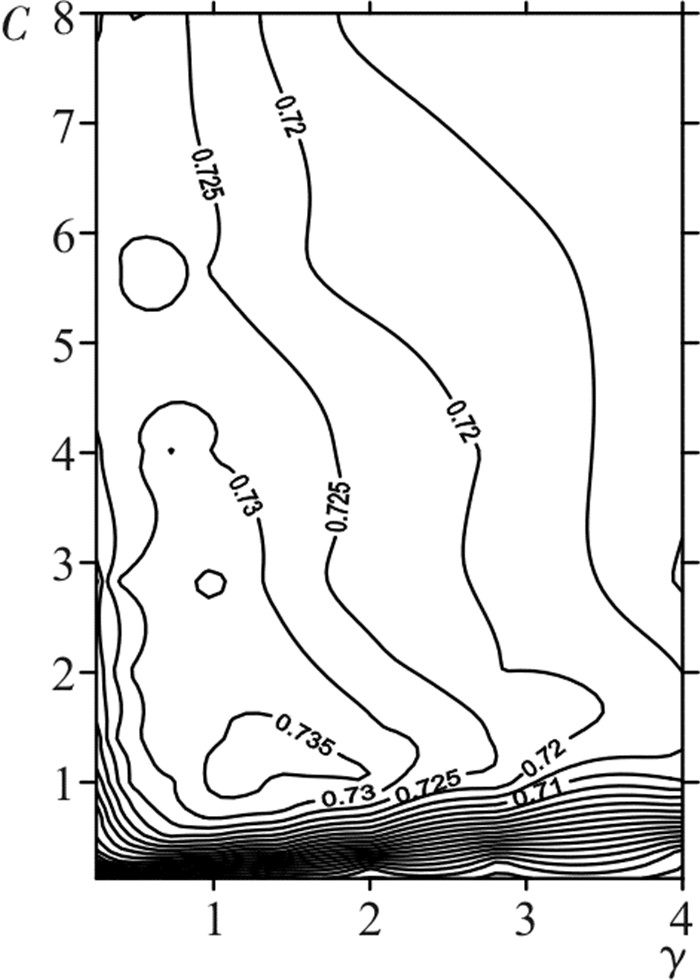
对训练数据集进行规范化处理，得到记录共2 435条。再将其分为10等份进行交叉验证，利用网格选优法获得不同(C，γ)组合下的预报准确率，绘制出模型精度与上述2个参数的关系图(图 1)。当C=2.83，γ=1.41时，模型交叉验证的精度达到最高值73.6%，筛选出了最佳的模型参数。
![]()
图 1 模型10折交叉验证的精度与参数对(C，γ)的关系图Figure 1. Relation between model accuracy of 10-fold cross-validation and parameter pair将筛选得到的参数代入模型重新训练，最终得到支持向量1 857个，其中标签为“是”渔场的支持向量734个，“非”渔场的支持向量1 123个。同时获得各个支持向量的系数ai(数量过多，略去)和b(0.489)值，从而获得了最优的SVM模型为：
$$ f(x)=\operatorname{sgn}\left(\sum\limits_{i=1}^{1857} y_i a_i \cdot \mathrm{e}^{-1.41\left\|x_i-x_j\right\|^2}+0.489\right) $$ (10) 2.2 渔场预报实例
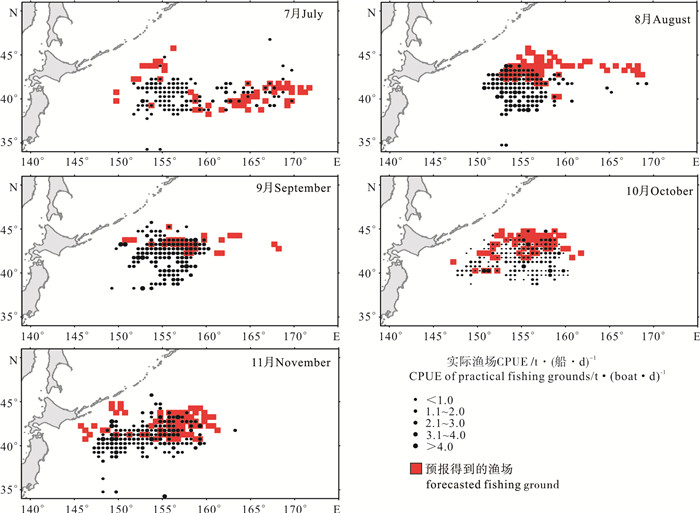
利用上节中得到的最优SVM模型，将2013年7年~11月的时空与环境数据进行规范化处理后代入式(8)中，得到各个月份的渔场预报结果。其中7月预报渔场呈条带状分布，经向跨度为150°E~175°E，8月预报渔场北移，最北端达到45°N，9月预报渔场分布形状与8月相近，但分布范围达到最小。10月和11月预报渔场开始向西南方向移动，161°E以东不再有渔场出现。将各个月份的预报渔场与2013年实际生产的渔场相叠加，得到图 2所示结果。
![]()
图 2 2013年实际渔场与SVM模型预报渔场对比图Figure 2. Comparison of practical fishing grounds and forecasted grounds by SVM in 20132.3 预报精度的检验
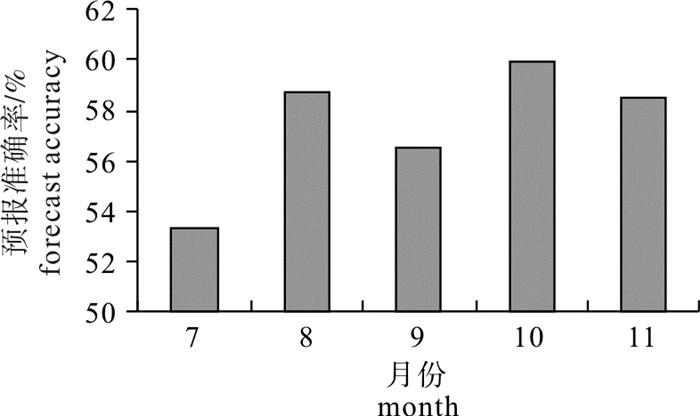
利用1.2.3节中渔场预报精度的检验公式，分别计算2013年7月到11月的渔场预报准确率，结果见图 3。其中预报准确率最高为10月(60.0%)，最低为7月(53.3%)，平均准确率为57.4%。
![]()
图 3 2013年7月~11月柔鱼渔场预报的综合准确率Figure 3. Comprehensive accuracies of O. bartramii fishing ground forecast from July to November in 20133. 讨论
西北太平洋柔鱼属于外洋性头足类，5月~8月未成熟的柔鱼向北或东北洄游，进入35°N~40°N黑潮与亲潮交汇区，8月~10月主要分布在40°N~60°N亲潮前锋区及其周围海域。10月~11月以后柔鱼达到性成熟，并伴随亲潮冷水团的扩展开始向南洄游[27]，其捕捞旺季集中在7月~11月之间，显然训练样本在渔场空间分布和渔汛长度上都有一定的限制。通过2013年柔鱼渔场的实际预报表明，SVM模型很好地克服了样本量不足的困难，取得了一定的预报效果。
柔鱼作为一年内完成整个生命周期的海洋生物，极易受外界环境的影响[28-29]。其中SST是影响柔鱼分布最重要的环境因子。陈新军等[30]通过对1995年~2001年北太平洋柔鱼渔场与SST数据分析发现，其产量在不同月份与不同海区的最适水温均有所不同。在150°E以西的海域，7月~11月的最适宜水温分别为17~19 ℃、18~22 ℃、17~19 ℃、13~18 ℃与10~14 ℃；在150°E~165°E的海域，6月~11月最适水温则分别12~14 ℃、14~17 ℃、15~19 ℃、14~18 ℃、12~15 ℃与10~13 ℃；而在更靠东部的165°E~180°E海域，6月~7月的最适水温则只有11~15 ℃。另外，叶绿素是另一个影响渔场的环境要素，沈新强等[30]研究发现北太平洋表层叶绿素a浓度的分布与柔鱼中心渔场的位置存在着较好的对应关系。在西部海域，柔鱼的渔场分别位于叶绿素a质量浓度在0.1 mg · m-3等值线舌状区域和叶绿素a水平梯度较高位置，渔场中心的叶绿素a质量浓度值大于0.1 mg ·m-3；而在中部海域，柔鱼渔场则位于叶绿素a水平梯度最大处；在东部海域，柔鱼渔场则位于0.1 mg · m-3叶绿素a质量浓度等值线舌状的右侧。除SST与叶绿素a外，两者在水平方向上形成的锋面，同样对柔鱼渔场有较大影响。YATSU等[32]研究表明当亚北极边界处出现一个较强的锋面时，柔鱼会出现较高的CPUE，并且会在向北的洄游中聚集在此强锋面水域。ICHII等[33]则认为柔鱼产卵场位置变化和洄游分布与过渡区叶绿素a锋面变动有关。鉴于此，该研究使用了SST、叶绿素a浓度以及SST和叶绿素a浓度梯度强度作为模型的解释变量具有合理性。
由于西北太平洋主要受到黑潮、亲潮2个海洋流系的影响，形成了较为复杂的海洋环境[34]，过去对该海域柔鱼渔场预报和资源变化的研究也多通过构建模型进行。如TIAN等[11]基于HSI模型，利用包括次表层水温在内的多个环境变量计算得到了2005年与2006年的柔鱼冬春生群体渔场预报结果；IGARASHI等[12]也用相同模型对2012年北太平洋东部海域柔鱼秋生种群的渔场实施了预报。由于HSI模型中可以选择不同的方法计算栖息地综合指数，因此在使用过程中表现出了较高的灵活性，HSI模型计算得到的预测结果并不是一个真实的概率值，因此与实际渔场并不存在严格的相关性[35]。SVM模型得到的渔场预报结果是一个离散值，即渔场的“是”与“非”，不存在一个连续型的概率概念，因此在实际应用中渔场预报结果更为明确和直观。另外，崔雪森等[19]利用朴素贝叶斯模型(Naïve Bayes)同样对该海域的柔鱼渔场预报模型进行了构建，并对2012年实际渔场进行了预报。由于朴素贝叶斯模型使用的前提是要求输入变量满足相互条件独立，所以首先要对环境数据等输入变量进行独立成分分析，这无疑增加了模型应用的复杂性。而SVM模型对解释变量只需要进行简单的规范化处理，原理更加简明，实现更为简单，因此利于在实际生产中推广和应用。与该研究的模型精度相比，HSI模型的预测预报精度值通常更高，在某些情况下可使几近90%的渔获落在HSI大于0.6的预测海域[11]，但在改变HSI阈值的情况下，会使统计精度产生较大的变化。这与该研究中式(9)的精度计算原理完全不同，因此通过预报精度值对两模型的优劣做出比较很困难。同时，与SVM模型类似，多数预报模型在不同月份的预报精度变动范围通常较大。如利用HSI模型对阿根廷滑柔鱼西南大西洋渔场的预报中，其2009年中心渔场预报准确率在57% ~74%之间波动[36]，崔雪森等[19]利用朴素贝叶斯模型对2012年北太平洋柔鱼渔场预报精度也为64% ~75%，这可能与一年中不同月份柔鱼类对海洋环境适应范围发生变化有关。
从总体叠加图上看，尽管SVM模型的2013年预报结果在空间分布上与实际渔场具有一定的一致性，但其精度的检验量化结果并不理想(图 3)。这其中除了模型本身存在的原因外，还可能有2个问题：1)有记录的作业海区并不能代表整个北太平洋海域中柔鱼的真实分布状况。出于利益考虑，商业捕捞渔船多集中于高产渔区，而当遇到产量下降时往往迅速转移渔场[17]。另外，渔业数据大多只重视存在渔获量的地点，而对于没有渔获量地点的记录并不重视[35]。这些都无疑会影响到模型的预报验证精度检验。2)精度检验方法未考虑渔区之间的空间关系。各个渔区在空间位置上存在着一定拓扑关系，而预报精度公式中却忽略了这种关系，只是单纯考虑各个渔区的预报结果与对应渔区的实际情况是否相符。实践证明，这种孤立地考虑各个渔区预报精度的方法，并不能全面地体现出模型的预报效果。如在该研究中，2013年7月的综合预报精度相当低，但预报渔场的分布与很多实际作业渔区相当接近，而这些都无法在精度评价公式中得到体现。因此，改进预报精度评价方法也是一个值得考虑的问题。
SVM原理较为简单，可以利用已知的有效算法获得目标函数的全局最小值，从而克服了可能陷入局部最优解的缺点。但SVM属于典型的“黑箱”模型方法，与某些更为直观的“白箱”模型(如分类决策树模型、GAM模型等)相比，要解释不同环境因子(输入变量或解释变量)如何影响、在何种程度上影响渔场的分布(输出变量)，是相当困难的。而准确的渔情预报须建立在对目标鱼种种群状况和渔场形成机制的了解和把握的基础上[35]，这对于模型的不断改进起着重要的作用。解决这个难题的一种常见方法是敏感度分析(sensitivity analysis)。特别是当时空变量以及环境变量数目过多时，通过灵敏度分析，可以选择出对模型影响最大的若干个变量，从而降低预报模型的复杂性，增强其在渔场预报中的实用性，这将是下一步研究工作之一。
4. 结论
该研究基于支持向量机的方法，以径向基函数为核函数，以中国在北太平洋的柔鱼渔获数据和海洋环境信息为训练数据集，建立了北太平洋柔鱼渔场预报模型，并使用10折交叉验证和网格选优的方法确定了模型中的最佳参数。在此基础上，利用2013年7月~11月环境数据，对模型进行了精度检验，取得了一定的预报效果。由于该算法在有限样本下学习能力，并且在实际应用中表现出了良好的适应性，相信其在今后的渔业研究中的应用范围会越来越广泛。
-
![]()
图 1 模型10折交叉验证的精度与参数对(C，γ)的关系图
Figure 1. Relation between model accuracy of 10-fold cross-validation and parameter pair
![]()
图 2 2013年实际渔场与SVM模型预报渔场对比图
Figure 2. Comparison of practical fishing grounds and forecasted grounds by SVM in 2013
![]()
图 3 2013年7月~11月柔鱼渔场预报的综合准确率
Figure 3. Comprehensive accuracies of O. bartramii fishing ground forecast from July to November in 2013
表 1 解释变量的规范化参数
Table 1 Parameters of explanatory variables for normalization
月份
month经度/°
longitude纬度/°
latitude海表温度
SST叶绿素a浓度
ChlSST梯度强度
intensity of SST gradientChl梯度强度
intensity of Chl gradient中心值center 9.066 9 155.516 1 42.226 8 16.167 4 0.427 6 0.019 8 0.002 2 变化幅度scale 1.308 6 4.456 4 1.582 4 3.190 0 0.279 1 0.012 0 0.002 5 
下载: 导出CSV
-
[1] YATSU A, TANAKA H, MORI J. Population structure of the neon flying squid, Ommastrephes bartramii, in the North Pacific[C]//Contributed Papers to International Symposium on Large Pelagic Squids. Tokyo: Japan Marine Fishery Resources Research Center, 1998: 31-48.
[2] CHEN C S, CHIU T S. Variations of life history parameters in two geographical groups of the neon flying squid, Ommastrephes bartramii, from the North Pacific[J]. Fish Res, 2003, 63(3): 349-366. doi: 10.1016/S0165-7836(03)00101-2
[3] 陈新军, 曹杰, 刘必林, 等. 基于贝叶斯Schaefer模型的西北太平洋柔鱼资源评估与管理[J]. 水产学报. 2011, 35(10): 1573-1581. http://scxuebao.ijournals.cn/scxuebao/article/abstract/20110307410 [4] CHEN X, LIU B, CHEN Y. A review of the development of Chinese distant-water squid jigging fisheries[J]. Fish Res, 2008, 89(3): 211-221. doi: 10.1016/j.fishres.2007.10.012
[5] 刘金立, 陈新军, 李纲, 等. 西北太平洋柔鱼资源综合配置模型及管理策略探讨[J]. 海洋与湖沼, 2014, 45(5): 1016-1021. http://qdhys.cnjournals.com/hyyhze/ch/reader/view_abstract.aspx?file_no=20130800115&flag=1 [6] SILVA C, NIETO K, BARBIERI M A, et al. Expert systems for fishing ground prediction models: a management tool in the humboldt ecosystem affected by ENSO[J]. Investig Mar, 2002, 30(1): 201-204. doi: 10.4067/S0717-71782002030100088
[7] FAN W, WU Y, CUI X. The study on fishing ground of neon flying squid, Ommastrephes bartrami, and ocean environment based on remote sensing data in the Northwest Pacific Ocean[J]. Chin J Ocean Limnol, 2009, 27(2): 408-414. doi: 10.1007/s00343-009-9107-1
[8] 陈新军, 刘必林, 田思泉, 等. 利用基于表温因子的栖息地模型预测西北太平洋柔鱼渔场[J]. 海洋与湖沼, 2009, 40(6): 707-713. doi: 10.3321/j.issn:0029-814X.2009.06.006 [9] 郑波, 陈新军, 李纲. GLM和GAM模型研究东黄海鲐资源渔场与环境因子的关系[J]. 水产学报, 2008, 32(3): 379-386. doi: 10.3321/j.issn:1000-0615.2008.03.008 [10] 崔雪森, 伍玉梅, 张晶, 等. 基于分类回归树算法的东南太平洋智利竹荚鱼渔场预报[J]. 中国海洋大学学报, 2012, 42(7/8): 53-59. [11] TIAN S Q, CHEN X J, CHEN Y, et al. Evaluating habitat suit-ability indices derived from CPUE and fishing effort data for Ommatrephes bratramii in the northwestern Pacific Ocean[J]. Fish Res, 2009, 95: 181-188. doi: 10.1016/j.fishres.2008.08.012
[12] IGARASHI H, AWAJI T, ISHIKAWA Y, et al. Development of a habitat suitability index model for neon flying squid by using 3-D ocean reanalysis product and its practical use[J]. JAMSTEC Rep Res Dev, 2014, 18: 89-101. doi: 10.5918/jamstecr.18.89
[13] 陈雪忠, 樊伟, 崔雪森, 等. 基于随机森林的印度洋长鳍金枪鱼渔场预报[J]. 海洋学报, 2013, 35(1): 158-164. doi: 10.3969/j.issn.0253-4193.2013.01.018 [14] 杨铭霞, 陈新军, 冯永玖, 等. 利用多种空间插值法分析西北太平洋柔鱼渔场[J]. 南方水产科学, 2015, 11 (2): 79-84. doi: 10.3969/j.issn.2095-0780.2015.02.011 [15] 袁红春, 顾怡婷, 汪金涛, 等. 西北太平洋柔鱼中长期预测方法研究[J]. 海洋科学, 2013, 37(10): 65-70. [16] 汤鸿益. 基于先验知识的SVM模型及渔业应用研究[D]. 上海: 上海海洋大学, 2011: 40-41.https://www.zhangqiaokeyan.com/academic-degree-domestic_mphd_thesis/020314222560.html [17] TIAN S, CHEN X, CHEN Y, et al. Standardizing CPUE of Ommastrephes bartramii for Chinese squid-jigging fishery in the northwest Pacific Ocean[J]. Chin J Ocean Limnol, 2009, 27(4): 729-739. doi: 10.1007/s00343-009-9199-7
[18] ISMAIL A I, MORRISON E C, BURT B A, et al. Natural history of periodontal disease in adults: findings from the Tecumseh Periodontal Disease Study, 1959-87[J]. J Dent Res, 1990, 69(2): 430-435. doi: 10.1177/00220345900690020201
[19] 崔雪森, 唐峰华, 张衡, 等. 基于朴素贝叶斯的西北太平洋柔鱼渔场预报模型的建立[J]. 中国海洋大学学报, 2015, 45(2): 37-43. doi: 10.16441/j.cnki.hdxb.20130413 [20] CHEN X, TIAN S, GUAN W. Variations of oceanic fronts and their influence on the fishing grounds of Ommastrephes bartramii in the Northwest Pacific[J]. Acta Oceanol Sin, 2014, 33(4): 45-54. doi: 10.1007/s13131-014-0452-3
[21] 于杰, 李永振. 海洋渔业遥感技术及其渔场渔情应用进展[J]. 南方水产, 2007, 3 (1): 62-68. doi: 10.3969/j.issn.2095-0780.2007.01.011 [22] PI Q, HU J. Analysis of sea surface temperature fronts in the Taiwan Strait and its adjacent area using an advanced edge detection method[J]. Sci China Earth Sci, 2010, 53(7): 1008-1016. doi: 10.1007/s11430-010-3060-x
[23] LECUN Y, BOTTOU L, ORR G B, et al. Efficient BackProp[J]. Lect N COMP, 1998, 1524(1): 9-50. doi: 10.1007/978-3-642-35289-8_3
[24] VAPNIK V N. The nature of statistical learning theory[M]. New York: Spring-Verlag, 1995: 138-153. doi: 10.1007/978-1-4757-3264-1
[25] HSU C, CHANG C, LIN C. A practical guide to Support Vector Classification[EB/OL]. (2015-03-13)[2015-06-01]. http://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html.
[26] 张衡, 崔雪森, 樊伟. 基于遥感数据的智利竹筴鱼渔场预报系统[J]. 农业工程学报, 2012, 28(15): 140-144. http://www.tcsae.org/cn/article/id/20121522 [27] 王尧耕, 陈新军. 世界大洋性经济柔鱼类资源及其渔业[M]. 北京: 海洋出版社, 2005: 145. https://www.zhangqiaokeyan.com/book-cn/08150423.html [28] RODHOUSE P G. Managing and forecasting squid fisheries in variable environments[J]. Fish Res, 2006, 54(1): 3-8. https://www.sciencedirect.com/science/article/abs/pii/S0165783601003708
[29] YATSU A, WATANABE T, MORI J, et al. Interannual variability in stock abundance of the neon flying squid, Ommastrephes bartramii, in the North Pacific Ocean during 1979-1998: impact of driftnet fishing and oceanographic conditions[J]. Fish Oceanogr, 2000, 9(2): 163-170. doi: 10.1046/j.1365-2419.2000.00130.x
[30] 陈新军, 田思泉. 西北太平洋海域柔鱼的产量分布及作业渔场与表温的关系研究[J]. 青岛海洋大学学报, 2005, 35(1): 101-107. doi: 10.3969/j.issn.1672-5174.2005.01.020 [31] 沈新强, 王云龙, 袁骐, 等. 北太平洋鱿鱼渔场叶绿素a分布特点及其与渔场的关系[J]. 海洋学报, 2004, 26(6): 118-123. doi: 10.3321/j.issn:0253-4193.2004.06.013 [32] YATSU A, WATANABE T. Interannual variability in neon flying squid abundance and oceanographic conditions in the central North Pacific, 1982-1992[J]. Bull Nat Res Inst Far Seas Fish, 1996(33): 123-138.
[33] ICHⅡ T, MAHAPATRA K, SAKAI M, et al. Differing body size between the autumn and the winter-spring cohorts of neon flying squid (Ommastrephes bartramii) related to the oceanographic regime in the North Pacific: a hypothesis[J]. Fish Oceanogr, 2004, 13(5): 295-309. doi: 10.1111/j.1365-2419.2004.00293.x
[34] MUGO R M, SAITOH S I, TAKAHASHI F, et al. Evaluating the role of fronts in habitat overlaps between cold and warm water species in the western North Pacific: a proof of concept[J]. Deep-Sea Ⅱ, 2014, 107: 29-39. https://www.sciencedirect.com/science/article/abs/pii/S096706451300444X
[35] 陈新军, 高峰, 官文江, 等. 渔情预报技术及模型研究进展[J]. 水产学报, 2013, 37(8): 1270-1280. doi: 10.3724/SP.J.1231.2013.38313 [36] 高峰, 陈新军, 范江涛, 等. 西南大西洋阿根廷滑柔鱼中心渔场预报的实现及验证[J]. 上海海洋大学学报, 2011, 20(5): 754-758. http://shhydxxb.ijournals.cn/shhy/article/abstract/201101115 -
期刊类型引用(9)
1. 解明阳，柳彬，陈新军. 基于深度学习的西北太平洋柔鱼渔场预测. 水产学报. 2024(11): 61-72 . 
百度学术
2. 曹睿星，官文江，高峰，贺伟伟. 基于最大熵和栖息地指数模型预测东、黄海日本鲭渔场分布. 海洋学报. 2023(09): 72-81 . 百度学术
3. 周文英，史文崇. 机器学习在渔业研究中的应用进展与展望. 渔业研究. 2022(04): 407-414 . 百度学术
4. 程懿麒，张俊波，汪金涛，雷林. 基于神经网络的印度洋长鳍金枪鱼(Thunnus alalunga)时空分布与海洋环境关系研究. 海洋与湖沼. 2021(04): 960-970+1-6 . 百度学术
5. 袁红春，王敏，刘慧，陈冠奇. 基于特征交互与卷积网络的渔场预测模型. 江苏农业学报. 2021(06): 1501-1509 . 百度学术
6. 李佳佳，汪金涛，陈新军，雷林，关长涛. 不同气候模态下西北太平洋柔鱼冬春生群资源时空分布变化研究. 南方水产科学. 2020(02): 62-69 . 本站查看
7. 侯娟，周为峰，樊伟，张衡. 基于集成学习的南太平洋长鳍金枪鱼渔场预报模型研究. 南方水产科学. 2020(05): 42-50 . 本站查看
8. 崔雪森，周为峰，唐峰华，戴阳，张胜茂，程田飞. 基于约束线性回归的柔鱼栖息地指数渔场预报模型构建. 渔业科学进展. 2018(01): 64-72 . 百度学术
9. 薛嘉伦，樊伟，唐峰华，郭刚刚，汤伟，张胜茂. 基于最大熵模型预测西北太平洋公海鲐潜在栖息地分布. 南方水产科学. 2018(01): 92-98 . 本站查看
其他类型引用(8)
计量
- 文章访问数: 3196
- HTML全文浏览量: 177
- PDF下载量: 1020
- 被引次数: 17
粤公网安备 44010502001741号
