A performance comparison of stock density estimation of Larimichthys polyactis in the East China Sea using different models based on bottom trawl survey
-
摘要:
单位捕捞努力渔获量(catch per unit effort,CPUE)是衡量资源丰度的相对指标,其均值的估算是渔业资源评估与管理中一项极为重要的基础性工作。文章以2004年~2006年东海区底拖网大面定点调查渔获的小黄鱼(Larimichthys polyactis)为例,利用算术平均值法、重抽样估值法、对数正态分布法、Δ-分布的最小方差无偏估计法和Finney-Sichel估值法分别对小黄鱼资源密度数据进行标准化处理,并评估不同方法的相对优劣性和稳健性。结果表明,基于对数正态分布的3种方法的均值估值较大,尤以Δ-分布法最大,而算术平均值法和重抽样估值法估值较小,且均值较接近;两两配对样本t检验显示,Δ-分布法的估值显著高于其他方法的结果(P < 0.05),而其余4种估值结果并无显著性差异(P>0.05);Δ-分布法和重抽样估值法的变异系数较接近,均小于其他结果;结合小黄鱼空间分布的特征及大面积调查自身特点,Δ-分布法被认为是5种估值方法中适用性和稳健性最好的方法。
Abstract:Estimation of average catch per unit effort (CPUE) which is a relative index to measure fish abundance is important foundational work for stock assessment and fishery management. Based on the data of Larimichthys polyactis collected from the bottom trawl survey conducted in the East China Sea from 2004 to 2006, we calculated the average stock density of L.polyactis by arithmetic mean estimator (AM), resampling mean estimator (RM), lognormal distribution mean estimator (LM), Δ-distribution mean estimator (DM) and Finney-Sichel mean estimator (FM), and evaluated the superiority (or inferiority) and robustness of different estimators. Results indicate that the mean estimators based on lognormal distribution were bigger than the last two estimators, and the Δ-distribution mean estimator was the biggest one, while the last two estimators were much closer. The paired-sample t test reveals that the Δ-distribution mean estimator was bigger than the other four estimators (P < 0.05);meanwhile, there was no difference among the other four estimators (P>0.05). The coefficient variation (CV) of the Δ-distribution mean estimator and the resampling mean estimator were less than the other three estimators. It is concluded that Δ-distribution mean estimator was the best estimation method with good applicability and robustness.
-
底拖网调查可为渔业资源评估与管理提供重要信息,是一种传统的、并被广泛应用的渔业资源调查与评估方法[1]。单位捕捞努力量渔获量(catch per unit effort,CPUE)大小常被作为资源丰度的相对指数来反映资源丰度的变化[2],在渔业资源评估和渔业管理中占据非常重要的地位。CPUE的标准化是渔业资源评估的重要研究内容,针对底拖网作业方式的CPUE标准化问题,国内外学者进行了大量的研究。目前,基于底拖网调查数据的处理与分析主要有2类方法: 1)基于调查设计的方法[3-4],如大面定点调查法;2)基于模型的方法,如对数正态分布模型[5],负二项分布模型[6],Gamma分布模型[7],Poisson分布模型[8],以及在对数正态分布模型基础上发展的Δ-分布模型[9-10]等。中国一些学者利用上述方法在不同水域开展了相关的应用研究[11-14],但上述方法总有一个前提假设,即底拖网调查数据服从某种特定的概率分布类型(如正态分布或对数正态分布),而事实上鱼类的空间分布究竟严格服从何种分布类型尚未明确。为此,文章引入另一种方法——重抽样估值法,即利用中心极限定理,在总体分布类型未知的情形下,根据原始样本复制观测信息,通过有放回重抽样对总体的分布特征进行统计推断的方法。文章拟根据东海区渔业资源底拖网大面定点调查资料,以小黄鱼(Larimichthys polyactis)为目标鱼种,对比分析其资源密度均值估计的算术平均值法、重抽样估值法、对数正态分布法、Δ-分布的最小方差无偏估计法和Finney-Sichel估值法之间的统计差异,以期寻找一种相对合理的CPUE标准化方法,从而提高资源评估的合理性和准确性,为以后中国渔业研究者准确估算资源量提供参考。
1. 材料与方法
1.1 数据来源
小黄鱼各站位原始资源密度(CPUE)取自2004~2006年春季(4月)、夏季(6月)、秋季(9月)和冬季(12月)东海区渔业资源底拖网大面定点调查资料。调查网具规格为100目×4 m·88 m-1,网囊网目为25 mm,拖速3 kn;调查范围为27°00′N~34°00′N、禁渔区线以东~127°00′E,站点以0.5°×0.5°栅格状设置,各年度调查航次和设计调查站位数均有差异,实际调查航次和相应站位数见表 1;调查船只通常是在24 h昼夜不间断地进行调查,每站位渔获随机取样1箱(15 kg),不足1箱全取,带回实验室鱼种分类、鉴定和渔业生物学测定,原则上每站拖曳时间设定为1 h,不足1 h或超过1 h均标准化为单位小时渔获量(kg·h-1),以此作为被分类鱼种的原始CPUE。
1.2 资源密度均值和方差估计
1.2.1 算术平均值法
假设总体服从正态分布,根据正态分布的数字特征,其均值和方差的表达式依次为:
$$ \overline X = \frac{{\sum\limits_{i = 1}^n {{X_i}} }}{n} $$ (1) $$ Var(X) = \frac{{\sum\limits_{i = 1}^n {{{({X_i} - \overline X )}^2}} }}{{n - 1}} $$ (2) 其中Xi是第i站的资源密度(kg·h-1),i=1, 2, …n,n是调查总站位数,包括渔获量为零值的站位。
1.2.2 重抽样估值法
根据中心极限定理,一个具有任意函数形式的总体,其样本均值μ和方差σ2有限。在对该总体进行有放回抽样时,随着样本量n的增大,由这些平均样本算出的均值的抽样分布将近似服从均值为μ和方差为$\frac{\mathsf{σ}^2}{n}$的正态分布[15]。均值的重抽样过程由Bootstrap法完成[16]。为减小功效损失,所选取的Bootstrap重抽样次数通常为499、999、4 999、9 999等,保证α×(N+1)为整数,其中α是名义显著性水平,取0.05,N是Bootstrap重抽样次数[17]。该研究选取N=4 999次,重抽样均值和方差的表达式依次为:
$$ \overline X = \frac{{\sum\limits_{j = 1}^N {{{\overline X }_j}} }}{N} $$ (3) $$ Var(\mathsf{CPUE}) = \frac{{{\mathsf{σ} ^2}}}{n} $$ (4) 其中X j由式(1)求得,它指第j组Bootstrap样本的均值,j=1, 2, …N。
1.2.3 对数正态分布法
假设总体服从对数正态分布,即若某随机变量的对数服从正态分布,则该随机变量服从对数正态分布。针对资源密度出现零值的问题,采用ln(x+1)进行标准化[18]。设μ和σ2分别表示资源密度中对数转换后的均值和方差,则对数正态分布的均值和方差表达式依次为:
$$ \bar{X}=\exp \left\{\mathsf{μ}+\frac{\mathsf{σ}^2}{2}\right\} $$ (5) $$ Var(X) = ({\rm{exp}}\left\{ {{{\rm{\mathsf{σ} }}^{\rm{2}}}} \right\} - 1) \bullet {\rm{exp}}\left\{ {{\rm{2\mathsf{μ} + }}{{\rm{\mathsf{σ} }}^{\rm{2}}}} \right\} $$ (6) 1.2.4 Δ-分布的最小方差无偏估计法
在对数正态分布理论基础上,为提高参数估计的精度,国外研究者给出了Δ-分布均值和方差的最小方差无偏估计式均值和方差的表达式[5, 9-10]为:
$$ \begin{array}{l} \overline X = \frac{m}{n}{\rm{exp}}(\overline Y ){g_m}(\frac{{\mathop S\nolimits_Y^2 }}{2}), m \ge 0, n > 0\\ \;Var(X) = \frac{m}{n}{\rm{exp}}(2\overline Y ) \bullet \end{array} $$ (7) $$ g_m\left(2 S_Y^2\right)-\frac{m-1}{n-1} g_m \frac{m-2}{m-1} S_Y^2 $$ (8) 式中m为渔获量为非零值的站位数,n意义同上,令Yi=ln(Xi),其中Xi>0;Y表示对数转换后资源密度的均值,$\mathop S\nolimits_Y^2 $表示对数转换后资源密度的方差;gm(t)为m和t的函数,其计算公式为:
$$ \begin{aligned} & \quad g_m(t)=1+\frac{m-1}{m} t+\sum\limits_{j=2}^{\infty} \frac{(m-1)^{2 j-1}}{m^j \prod\limits_{i=2}^j(m+2 i-3)} \\ & \frac{t^j}{j!} \end{aligned} $$ (9) 式(9)为一超几何分布函数。根据该无穷级数的收敛性,可知随着j值的增大,gm(t)趋近于一常数。
1.2.5 Finney-Sichel估值法
设Y、$\mathop S\nolimits_Y^2 $、n和gn(t)的意义与式(5)、(7)相同,资源密度为零值时,仍采用ln(x+1)进行标准化,m=n。则Finney-Sichel估值法的均值和方差的一致最小方差无偏估计式为[18-20]为:
$$ \bar{X}=\exp (\bar{Y}) g_n\left(\frac{S_Y^2}{2}\right) $$ (10) $$ {Var}(X)=\exp \{2 \bar{Y}\} \quad g_n\left(2 S_Y^2\right)-g_n\left(\frac{n-2}{n-1} S_Y^2\right) $$ (11) 1.3 统计分析
采用SPSS 18.0软件中单样本Kolmogorov-Smirnov检验验证不同年份、不同季节的小黄鱼资源密度数据是否服从正态分布,利用两两配对样本t检验分析不同估算方法的均值估值间是否存在显著性差异,P < 0.05表示数据间存在显著性差异。
2. 结果与分析
2.1 正态性检验
该研究中针对小黄鱼在大面积调查中某些站位未出现或无分布的情形,均以零计。考虑到自然对数的定义范围,文章仅对资源密度中非零值数据取自然对数,从而致使对原始数据和自然对数转换数据进行正态性检验时样本量出现差异(表 1)。利用SPSS 18.0软件分别对2004年~2006年四季节小黄鱼的各调查站位资源密度值和经自然对数转换后的资源密度值进行单样本Kolmogorov-Smirnov正态性检验显示,不同年份不同季节各调查站位小黄鱼的原始资源密度值的正态性双侧近似显著性概率值(P1)均小于0.05(表 1),从统计上判断,该组数据不服从正态分布;除2005年秋季外,原始数据中非零值经自然对数转换后的正态性双侧近似显著性概率(P2)范围为0.40~0.99,均大于0.05(表 1),表明经自然对数转换后的小黄鱼资源密度数据从统计上不否定其服从正态分布。
表 1 2004年~2006年小黄鱼调查站位数和出现站位数及原始资源密度值和对数转换值的正态性检验Table 1 Quantity of survey stations and appearance stations, one-sample Kolmogorov-Smirnov test for normality with untransformed and ln-transformed stock density of L.polyactis from 2004 to 2006季节
season2004 2005 2006 N1 P1 N2 P2 N1 P1 N2 P2 N1 P1 N2 P2 春季spring 115 < 0.01 62 0.57 111 < 0.01 70 0.96 121 < 0.01 76 0.57 夏季summer 107 < 0.01 63 0.99 111 < 0.01 43 0.98 117 < 0.01 62 0.40 秋季autumn 119 < 0.01 72 0.42 112 < 0.01 64 0.04 122 < 0.01 85 0.48 冬季winter 113 < 0.01 58 0.54 64 < 0.01 31 0.84 64 < 0.01 47 0.60 注:N1和N2分别表示总调查站位数和资源密度为非零值的调查站位数;P1和P2分别表示原始和自然对数转换后的资源密度值的正态性双侧近似显著性概率
Note:N1 and N2 represent the number of total survey stations and the stations with catch greater than zero; P1 and P2 indicate Asymp.Sig (2-tailed) for original and ln-transformed stock density data,respectively.2.2 不同估值方法间的差异
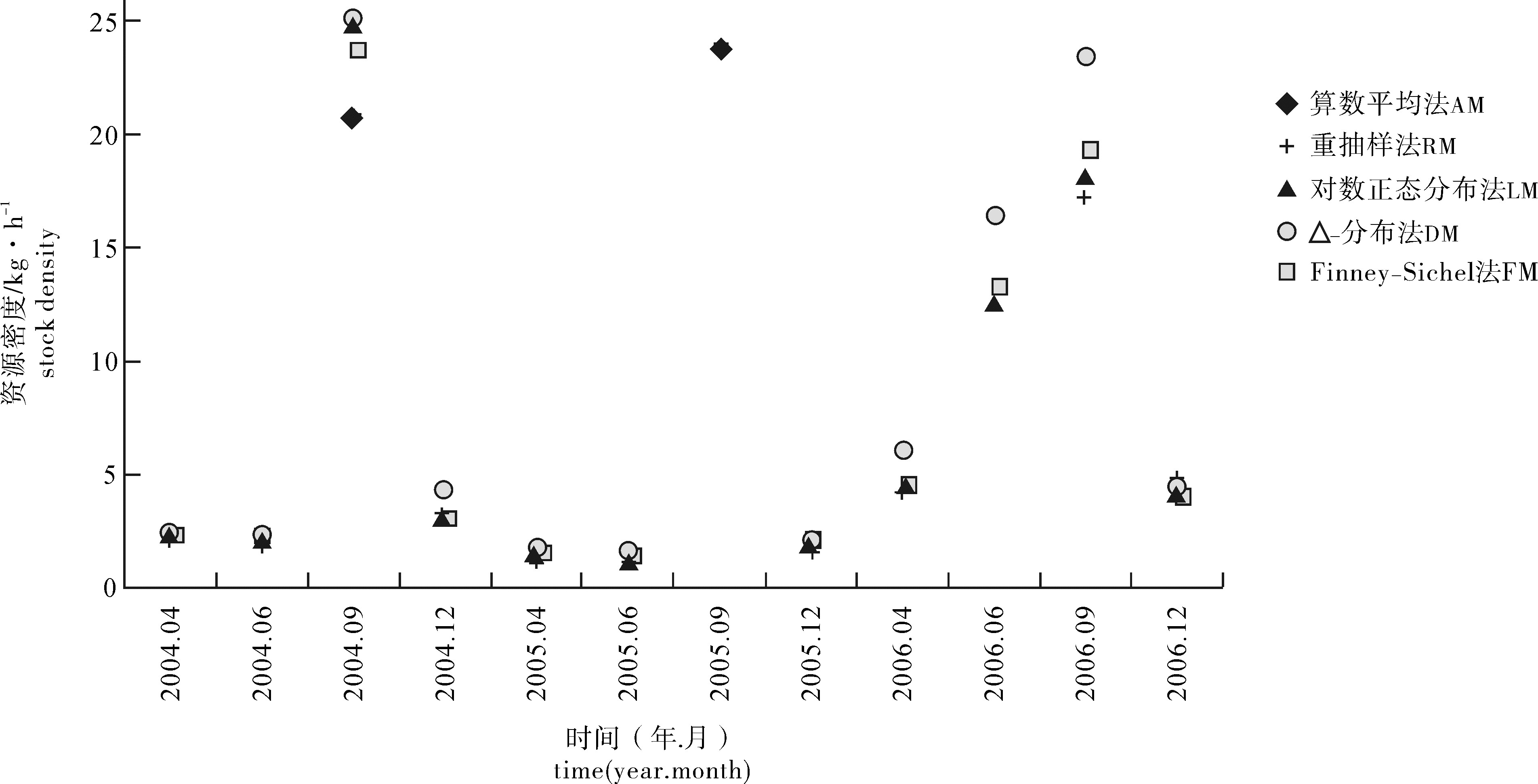
2004年~2006年四季节小黄鱼资源密度均值和方差的不同模型方法估值结果见图 1。整体上,基于对数正态分布的3种方法的均值估值结果较大,其中尤以Δ-分布的最小方差无偏估计法的估值结果最大,而算数平均值法和重抽样估值法的均值估值结果比较接近,均值小于上述3种方法的估值结果。为判断5种不同方法的估值结果在统计上是否存在显著差异,该研究将5种方法下估算的不同年份、相应季节的小黄鱼资源密度均值结果两两设定为待检验配对样本,利用两两配对样本t检验进行统一比较后发现,Δ-分布的最小方差无偏估计法的估值与其他4种估值方法存在显著性差异(P均小于0.05),而算术平均值法、重抽样估值法、对数正态分布法和Finney-Sichel估值法之间并无显著性差异(P均大于0.05)(表 2)。将不同估算方法下的不同年份、相应季节的小黄鱼资源密度估值结果依次两两设定为待检验配对样本,由于2005年9月的小黄鱼资源密度数据对数转后仍不服从正态分布,文章仅用了算术平均值法和重抽样估值法对其进行估算,估值结果表明,两者间差异甚小,前者的估值结果略小于后者。
表 2 不同估值方法间的两两配对样本t检验Table 2 T-test of paired samples by different modeling equations模型
model算术平均法
AM重抽样法
RM对数正态分布法
LMΔ-分布法
DMFinney-Sichel法
FMt P t P t P t P t P 算数平均法AM - - -1.78 0.11 -1.47 0.17 -2.81 0.02 -1.61 0.14 重抽样法RM 1.78 0.11 - - -1.07 0.31 -2.45 0.03 -1.02 0.33 对数正态法LM 1.47 0.17 1.07 0.31 - - -2.23 0.04 1.09 0.30 Δ-分布法DM 2.81 0.02 2.45 0.03 2.23 0.04 - - 2.62 0.03 Finney-Sichel法FM 1.61 0.14 1.02 0.33 -1.09 0.30 -2.62 0.03 - - 注:t. t检验统计量;P. 双侧检验显著性水平
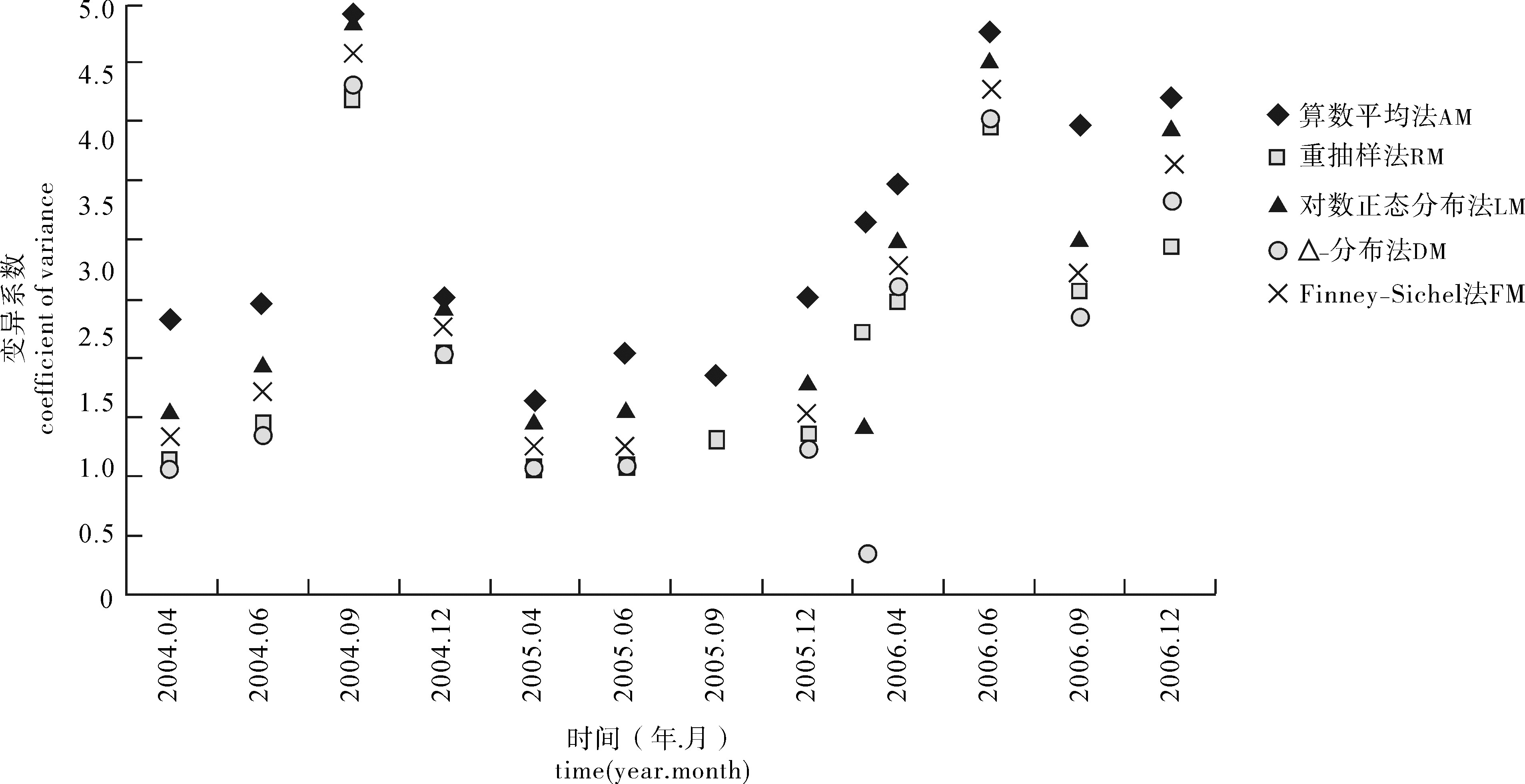
Note:t. t-test statistics; P. two-tailed significanceΔ-分布的最小方差无偏估计法的估值结果均大于其他4种方法的结果,为进一步检验不同估值方法的优劣性和稳健性,并从中选择一种较为适用的模型,文章选择变异系数这一统计指标来验证不同方法间的差异。结果表明,整体上,重抽样估值法和Δ-分布的最小方差无偏估计法的变异系数较为接近,且较其他3种方法更小,尤以重抽样估值法最小,Finney-Sichel估值法次之,再次为对数正态分布法,而算术平均值法的变异系数最大(图 2)。
3. 讨论
3.1 调查数据中零值的常用处理方法探讨
东海区渔业资源底拖网大面定点调查属于昼夜进行的多种类、大范围的综合性调查,受栖息地、环境、渔具适用性及鱼类行为特点等因素的影响,单一种类往往不会分布在整个调查水域且显不均匀分布特征。在数据处理过程中,将这些调查水域中无空间分布或由网具造成的调查站位中无目标鱼群出现的情况定义为零值。该研究中小黄鱼调查数据中零值出现比例为26.56%~61.26%,因此,讨论零值的处理方式非常必要。出现零值处理方式存在多种形式,常见的处理方式有以下几种:1)直接剔除零值;2)选用适当的概率分布模型,如负二项分布[7]、Poisson分布[8],尤其当零值较多时可选用Tweedie分布模型[21];3)不考虑原始数据的概率分布类型,直接利用再抽样过程进行CPUE标准化处理[22];4)包含零值的CPUE数据通常服从对数正态分布[18, 23],考虑到零值无法对数转换,常采用的方法是将CPUE原始数据加上一个常数,如加1[18]或CPUE均值的10%等[24],加常数后的CPUE数据亦可选择Gamma分布模型进行估计[7];5)源于正态分布基础上Δ-分布模型法和Finney-Sichel估值法在处理零值时具备一定的优势[5, 7, 11-14]。上述关于零值的不同处理方法,有其各自的适用条件,各有其优点缺陷,但目前尚无一种方法能较好地处理CPUE(包含零值)的均值估算问题,因此,在现有数据的基础上分析比较不同方法之间的优劣性和适用性是一项非常有意义的工作。该研究根据东海小黄鱼空间分布特征及最新研究成果,结合上述3)~5)等处理方式,对小黄鱼资源密度不同估算方法进行差异化分析。
3.2 不同估值方法间差异性分析
2004年~2006年四季节小黄鱼资源密度的原始数据经检验并不服从正态分布,因此使用基于正态分布基础上的算术平均值法不恰当(表 1)。而小黄鱼资源密度中非零值部分经自然对数转换后的正态性检验结果表明,该组数据从统计上基本服从正态分布。PENNINGTON[10]认为影响资源丰度的因子具有乘法效应,由中心极限定理知调查数据应服从对数正态分布,基于对数正态分布理论上的研究方法较算数平均法更具稳健性[10, 25]。源于重抽样理论基础上的Bootstrap方法是EFRON提出来的一种统计方法,它根据给定的原始样本复制观测信息,不需要进行分布假设或增加新的样本信息,可对总体的分布特征进行统计推断,属于非参数统计方法[26-27]。小黄鱼空间分布严格服从何种分布类型,目前尚无定论,而Bootstrap方法则无须考虑总体分布类型,应用于资源密度均值的估计不失为一种有意义的尝试。
变异系数是衡量资料中各观测值变异程度的一个统计量,当进行2个或多个资料变异程度比较时,如果均值不等时,需采用变异系数而非标准差来比较。利用5种不同估值方法对2004年~2006年四季节小黄鱼资源密度均值进行估算的结果可见,Δ-分布的最小方差无偏估计法均值的估值结果整体上较其他4种方法的结果稍大一些,且统计学检验表明,Δ-分布的最小方差无偏估计法的估值与其他4种估值方法存在显著性差异(P均小于0.05),而算术平均值法、重抽样估值法、对数正态分布法和Finney-Sichel估值法之间并不存在显著性差异(P均大于0.05)(图 1)。造成这一结果的原因有2个:1)对于资源密度频数分布呈右偏的情形,由于其不服从正态分布,中位数明显小于均值,使用算术平均法估算总体不仅造成评估效率较差而且低估了总体均值[10, 18-19],同时,Δ-分布法的均值估值高于算数平均法且是总体均值的最小方差无偏估计,评估效率较高,且满足统计上点估计的优良性准则;2)该研究中在使用对数正态分布法和Finney-Sichel估值法的估算均值时,对原始数据中较高比例的零值采用了ln(x+1)的转换后仍为零值,造成对数转换后的均值μ和Y偏小,致使该2种方法的均值估计值有所偏低,同时,SMITH[9]研究指出,由于x→0时ln(x)→- ∞,因此利用对数正态分布模型估计总体的稳健性较差。特别地,针对不服从对数正态分布理论的情形,如2005年秋季,文章仅采用算术平均值和重估值法进行估计。为进一步提高模型估算的稳健性和评判不同估值方法的优劣性,还需分析比较不同估值方法的方差大小,进而计算不同方法的变异系数。基于概率分布模型的4种方法中,Δ-分布的最小方差无偏估计法估值的变异系数最小,算数平均值估算结果最大,这说明Δ-分布法模型的稳健性较好,是4种方法中相对最优的模型(图 2)。结合鱼类资源密度频数分布呈右偏的特征,SMITH[9]、PENNING- TON[10]、MCCONNAUGHEY和CONQUEST[18]、SYRJALA[23]已经从理论和实践2个层面充分论证了Δ-分布法模型法的稳健性和合理性,而且这种方法也适于中国近海底拖网调查数据的评估[11-14]。ADDISCOTT[20]指出,基于对数正态分布理论上的Finney-Sichel估值法适用于频数分布为中度甚至高度偏斜的数据,当样本量较小或者方差较大时适合用;对于样本量较大(至少为30)且中度偏斜数据使用Δ-分布法更好。该研究进一步验证了Δ-分布法的优势,同时,国内外渔业工作者就此结论已做了大量实例分析和验证[20, 22, 28]。基于中心极限定理基础上的Bootstrap方法估值结果的变异系数较其他4种方法更小,而变异系数通常被认为是评估模型优劣的一个重要指标[28],因此,该方法从统计上是5种方法中相对最佳的模型。当原始数据既不服从正态分布,也不服从对数正态分布时,如2005年秋季小黄鱼调查数据,选用Bootstrap方法从理论上讲不失为一种可行的方法。但实施Bootstrap过程需要满足一个假设条件是所观测到的样本能较好地反映总体。1)由于东海区渔业资源大面调查是多种类调查,调查范围大、区域广,结合小黄鱼栖息分布的局限性及季节分布差异,造成了大量零值出现,且零值中大部分属于无栖息分布类型(30%~50%),剩余部分属于有栖息分布但调查中没有渔获的情况,LAMBERT[29]和SHONO[21]等提出应将2种不同形式的零值区分开来处理,因此,以大面调查原始数据并不能有效地反映总体分布特征;2)算术平均值法的估值相当于总体的一次抽样,是Bootstrap过程的一个子样本,而Bootstrap方法的估值结果是由大量的Bootstrap子样本得到,当重复抽样的次数趋于无穷大时,两者的均值是相等的。PENNINGTON[10]认为,海洋生物资源密度右偏分布的情形造成算术平均值法估算总体均值时的结果存在低估现象。而Bootstrap方法的估值结果是由其子样本通过算数平均法计算得来,其对总体均值的估算结果较真实值仍会偏低。因此,Bootstrap方法尽管在方差的估算上有显著降低,但因其在均值上与算数平均法较接近,故使用时需谨慎。
-
表 1 2004年~2006年小黄鱼调查站位数和出现站位数及原始资源密度值和对数转换值的正态性检验
Table 1 Quantity of survey stations and appearance stations, one-sample Kolmogorov-Smirnov test for normality with untransformed and ln-transformed stock density of L.polyactis from 2004 to 2006
季节
season2004 2005 2006 N1 P1 N2 P2 N1 P1 N2 P2 N1 P1 N2 P2 春季spring 115 < 0.01 62 0.57 111 < 0.01 70 0.96 121 < 0.01 76 0.57 夏季summer 107 < 0.01 63 0.99 111 < 0.01 43 0.98 117 < 0.01 62 0.40 秋季autumn 119 < 0.01 72 0.42 112 < 0.01 64 0.04 122 < 0.01 85 0.48 冬季winter 113 < 0.01 58 0.54 64 < 0.01 31 0.84 64 < 0.01 47 0.60 注:N1和N2分别表示总调查站位数和资源密度为非零值的调查站位数;P1和P2分别表示原始和自然对数转换后的资源密度值的正态性双侧近似显著性概率
Note:N1 and N2 represent the number of total survey stations and the stations with catch greater than zero; P1 and P2 indicate Asymp.Sig (2-tailed) for original and ln-transformed stock density data,respectively.表 2 不同估值方法间的两两配对样本t检验
Table 2 T-test of paired samples by different modeling equations
模型
model算术平均法
AM重抽样法
RM对数正态分布法
LMΔ-分布法
DMFinney-Sichel法
FMt P t P t P t P t P 算数平均法AM - - -1.78 0.11 -1.47 0.17 -2.81 0.02 -1.61 0.14 重抽样法RM 1.78 0.11 - - -1.07 0.31 -2.45 0.03 -1.02 0.33 对数正态法LM 1.47 0.17 1.07 0.31 - - -2.23 0.04 1.09 0.30 Δ-分布法DM 2.81 0.02 2.45 0.03 2.23 0.04 - - 2.62 0.03 Finney-Sichel法FM 1.61 0.14 1.02 0.33 -1.09 0.30 -2.62 0.03 - - 注:t. t检验统计量;P. 双侧检验显著性水平
Note:t. t-test statistics; P. two-tailed significance -
[1] KOTWICKI S, MARTIN M H, LAMAN E A. Improving area swept estimates from bottom trawl surveys[J]. Fish Res, 2011, 110(1): 198-206. doi: 10.1016/j.fishres.2011.04.007
[2] MAUNDER M N, PUNT A E. Standardizing catch and effort data: a review of recent approaches[J]. Fish Res, 2004, 70(2): 141-159. doi: 10.1016/j.fishres.2004.08.002
[3] COCHRAN W G. Sampling techniques[M]. 3rd ed. New York: John Wiley and Sons, 1977: 428.
[4] THOMPSON M E. Theory of sample designs[M]. London: Chapman and Hall, 1997: 93-135.
[5] AICHISON J, BROWN A C. The lognormal distribution, with special reference to its uses in economics[M]. Cambridge: Cambridge University Press, 1957: 176-179. doi: 10.2307/2985613
[6] PUNT A E, WALKER T I, TAYLOR B L, et al. Standardization of catch and effort data in a spatially-structured shark fishery[J]. Fish Res, 2000, 45(2): 129-145. doi: 10.1016/S0165-7836(99)00106-X
[7] WIENS B L. When lognormal and gamma models give divergent results: a case study[J]. Am Stat, 1999, 53: 89-93.
[8] VENABLES W N, DICHMONT C M. GAMs, GAMS and GLMMs: an overview of theory for applications in fisheries research[J]. Fish Res, 2004, 70(3): 319-337. doi: 10.1016/j.fishres.2004.08.011
[9] SMITH S J. Use of statistical models for the estimation of abundance from groundfish trawl design data[J]. Can J Fish Aquat Sci, 1990, 47: 894-903. doi: 10.1139/f90-103
[10] PENNINGTON M. Estimating the mean and variance from highly skewed marine data[J]. Fish Bull, 1996, 94(3): 498-505. https://d.wanfangdata.com.cn/periodical/Ch9QZXJpb2RpY2FsRU5HTmV3UzIwMjQwOTEwMTY1MjU1EiA0Yjg5MjcyYjc4Zjk5MmZkOTljYmExYTdiYmZkY2VlZRoIaXI5Ym5zeGg%3D
[11] 李凡, 李显森, 赵宪勇. 底拖网调查数据的Delta-模型分析及其在黄海小黄鱼和银鲳资源分布评估中的应用[J]. 水产学报, 2008, 32(1): 145-151. https://kns.cnki.net/kcms2/article/abstract?v=WStw-Pbchowt2rlquGseY0zGtXB2GWwmj8d3y49rg4GisfDq51zsKBBTBvERMBGBFjCH8seSfovTZIqMQpLwKB95uO8A_PDfSlZsEnHxJupcLJoChSl6E_YfiBucVGQJNLvALpWOrWVPE3Yvm6MdZVd0GT6rMIVfJqW6sTIxPcpGDLmmopbUne_onRi4cfD3&uniplatform=NZKPT&language=CHS [12] 袁兴伟, 姜亚洲, 严利平. 东海区刺鲳资源密度不同估算方法的差异比较[J]. 海洋渔业, 2009, 31(1): 10-15. doi: 10.3969/j.issn.1004-2490.2009.01.002 [13] 黄良敏, 李军, 张雅芝, 等. 闽江口及附近海域渔业资源现存量评析[J]. 热带海洋学报, 2010, 29(5): 142-148. doi: 10.3969/j.issn.1009-5470.2010.05.022 [14] 袁兴伟, 姜亚洲, 程家骅. 利用Δ-模型法评估调查数据带有极端值的渔业生物的平均资源密度[J]. 渔业科学进展, 2011, 32(1): 1-7. doi: 10.3969/j.issn.1000-7075.2011.01.001 [15] ZAR J. Biostattistical analysis[M]. 3rd ed. NJ. USA: Prentice-Hall. Englewood Cliffs, 1995: 710-718.
[16] EFRON B. Bootstrap methods: another look at the Jackknife[J]. Ann Stat, 1979, 7(1): 1-26. doi: 10.1214/AOS/1176344552
[17] 龙志和, 欧变玲. Bootstrap方法在经济计量领域的应用[J]. 工业技术经济, 2008, 27(7): 132-135. https://kns.cnki.net/kcms2/article/abstract?v=WStw-Pbchox_pfVWmrOwtXPDYKQJ5GQh3opgHuBjyJWqQx61JO7tBatoReUVYfqlGI6ZDKSJhYKQLLdnFKVezL1HSetSpx_dXhvs7ri3b_c6X95YAr1NTkc1-ZlEChgPbR6C_Ef9ALOP1LrYI98TS5s7o1dbu0G4U4Pt2waGoveSRKBzzk3Ly-PglCuHLiFE&uniplatform=NZKPT&language=CHS [18] MCCONAUGHEY R A, CONQUEST L L. Trawl survey estimation using a comparative approach based on lognormal theory[J]. Fish B-NOAA, 1993, 91(1): 107-118.
[19] PENNINGTON M. Efficient estimators of abundance, for fish and plankton surveys[J]. Biometrics, 1983, 39(1): 281-286. doi: 10.2307/2530830
[20] ADDISCOTT T M. That uncertain feeling: measuring and modeling nitrogen losses by leaching[R]. Canberra: LWRRDC (Land and Water Resources Research and Development Corporation), Occasional Paper No. 08, 1996: 6-22.
[21] SHONO H. Application of the Tweedie distribution to zero-catch data in CPUE analysis[J]. Fish Res, 2008, 93(1/2): 154-162. doi: 10.1016/j.fishres.2008.03.006
[22] PEREZ P, DEFEO O. Estimation of catchability for the Heterocarpus reedi and Cervimunida johni fisheries in northern Chile, using different catch per unit of area estimators[J]. Interciencia, 2005, 30(1): 19-23. https://kns.cnki.net/kcms2/article/abstract?v=WStw-Pbchoy81oDMATli74jIe2qTtqLrG3iRZYVoZ6IiMEQcgQFOJvg7Vf3BAivfYWlzFfQF0C2qvknDZLesK2Ko-MxkyZXzi631ZLsWWr-NrRnHbJmmKYAl5frA2jU9fybNvJFsjM8o6t-BhejspH5uuRzZbfC_pTHi0uTq82ioGhJZGsphYzDEjcF0ZhJDENbCq2AQBI4lBf9ocB1jXSB8sLrrzpXg&uniplatform=NZKPT&language=CHS
[23] SYRJALA S E. Critique on the use of the delta distribution for the analysis of trawl survey data[J]. ICES J Mar Sci, 2000, 57(4): 831-842. doi: 10.1006/jmsc.2000.0571
[24] CAMPBELL R A, TUCK G, TSUJI S, et al. Indices of abundance for southern bluefin tuna from analysis of fine-scale catch and effort data[C]. Working Paper No. 16 presented at the 2nd CCSBT Scientific Meeting, August 26-September 6, Hobart, Australia, 1996: 35.
[25] PENNINGTON M. On testing the robustness of lognormal-based abundance estimators[J]. Biometrics, 1991, 46(4): 1185-1192. https://www.semanticscholar.org/paper/ON-TESTING-THE-ROBUSTNESS-OF-LOGNORMAL-BASED-Pennington/466039f75433a486cae6918c8f1ac8272a0f878a
[26] MONEY C Z, DUVAL R D. Bootstrapping. A nonparametric approach to statistical inference[G]//Sage University paper series on quantitative applications in the social sciences. Sage: Newbury Park, 1993: 7-95. https://searchworks.stanford.edu/view/2749116
[27] 赵亮, 程锦秀, 许木启, 等. Bootstrap方法及其在生物学研究中的应用[J]. 四川动物, 2010, 29(4): 638-641. https://d.wanfangdata.com.cn/periodical/Ch9QZXJpb2RpY2FsQ0hJTmV3UzIwMjQxMTA1MTcxMzA0Eg1zY2R3MjAxMDA0MDM1GghvNWV5MnNnaQ%3D%3D [28] PARKIN T B, MEISINGER J J, CHESTER S T, et al. Evaluation of statistical estimation methods for lognormally distributed variables[J]. Soil Sci Soc Am J, 1988, 52(2): 323-329. doi: 10.2136/sssaj1988.03615995005200020004x
[29] LAMBERT D. Zero-inflated Poisson regression, with an application to defects in manufacturing[J]. Technometrics, 1992, 34(1): 1-14.
-
期刊类型引用(7)
1. 高峰,向劲,谢宜兴,邓智勇,陈家法,谢玉坤,欧东升,王崇瑞. 基于大型无脊椎动物群落多样性的张家界野生大鲵生境质量评价. 淡水渔业. 2023(01): 102-112 .  百度学术
百度学术
2. 晏然,范江涛,陈作志,蔡研聪,张魁,许友伟,徐姗楠. 南海北部近海竹荚鱼资源密度的概率分布型特征. 中国水产科学. 2019(01): 91-98 .  百度学术
百度学术
3. 陶雅晋,冯波,易木荣,李波,卢伙胜,颜云榕. 基于渔港抽样调查不同捕捞方式CPUE单位标准化新方法. 渔业科学进展. 2019(02): 15-24 .  百度学术
百度学术
4. 陶雅晋,易木荣,李波,冯波,卢伙胜,颜云榕. 基于渔港抽样调查南海不同捕捞方式CPUE比较分析. 渔业科学进展. 2019(03): 1-10 .  百度学术
百度学术
5. 郭建忠,陈作志,许友伟,徐姗楠,李纯厚. 大亚湾鱼类资源数量的时空分布特征. 中国海洋大学学报(自然科学版). 2018(12): 47-55 .  百度学术
百度学术
6. 刘健,张崇良,薛莹,徐宾铎,任一平. 黄河口两种鱼类资源密度不同估算方法的比较. 中国水产科学. 2017(04): 845-852 .  百度学术
百度学术
7. 王德虎,黄洪亮,李灵智,屈泰春,齐广瑞,宋学锋. 小黄鱼单层流刺网网目选择性研究. 河南农业科学. 2016(07): 127-131 .  百度学术
百度学术
其他类型引用(4)



 下载:
下载:
 粤公网安备 44010502001741号
粤公网安备 44010502001741号
