Simulation of flow field inside the net cleaning machine based on ANSYS
-
摘要:
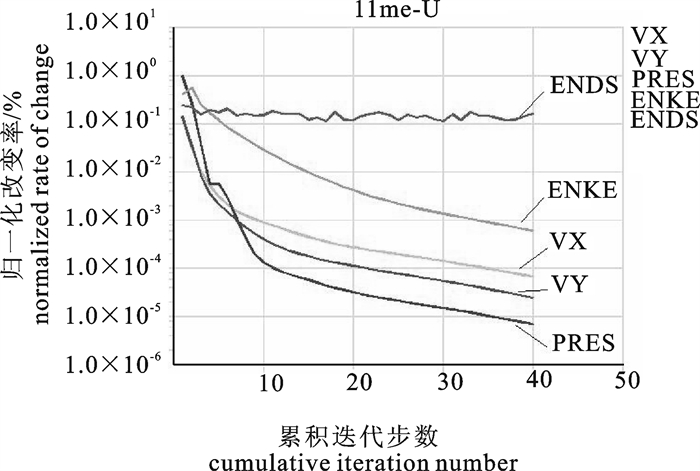
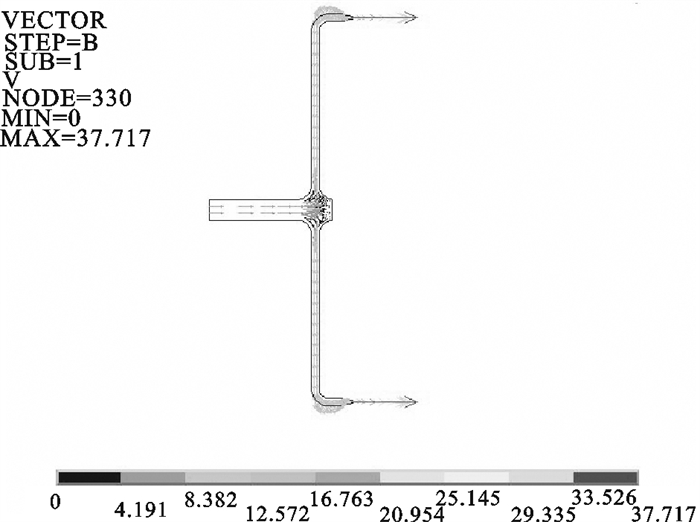
建立了水下洗网机内部流动的CFD计算模型，用计算流体力学软件ANSYS-FLOTRAN对水下洗网机内部的流场进行了模拟分析，得到了洗网机内部流体的速度分布曲线及压力分布曲线。分析结果为研究洗网机结构参数的优化设计提供了重要参考。
Abstract:The paper established a CFD simulation model of flow field inside the net cleaning machine, which was then analyzed by using CFD software of ANSYS-FLOTRAN. The distribution of flow velocity and that of flow pressure were obtained. The results provided important references for optimizing the structure of net cleaning machine.
-
Keywords:
- net cleaning machine /
- flow field /
- numerical simulation
-
福瑞鲤(Cyprinus carpio)以建鲤和黄河鲤为原始亲本，通过建立自交、正反交家系构成选育基础群体，用最佳线性无偏预测(best linear unbiased prediction，BLUP)分析获得个体的估算育种值，根据育种值大小和家系背景作为下一代亲本选配的标准，经过4代选育，获得了较大的遗传进展，生长性状得到显著提高，是农业部“十二五”主推的大宗淡水养殖鱼类新品种[1-2]。但作为人工育成的品种，仍需要不断地选育、保种和遗传保护，以防止种质退化，并培育出性状更加优良的新品系。
数量遗传学BLUP分析是测定种畜育种值的理想方法[3-4]，引进到水产动物育种后也取得很好的效果。如应用于国外水产动物尼罗罗非鱼(Oreochromis niloticus)[5]、大西洋鲑(Oncorhynchus kisutch)[6]、虹鳟(O.mykiss)[7]和鲤[8]等选择育种中的生长性状遗传参数评估。近年来，在国内大口黑鲈(Micropterus salmoides)[9]、大菱鲆(Scophthalmus maximus)[10]、大黄鱼(Larimichthys crocea)[11]、团头鲂(Megalobrama amblycephala)[12]和虹鳟[13]等经济鱼类的遗传参数估计中也取得很大进展。而运用大规模家系选育技术在水产动物中进行遗传改良在虹鳟[14]、罗非鱼[15-16]和鲤[1, 17-19]等经济鱼类中已得到很好的应用，并对不同家系斑点叉尾(Ictalurus punctatus)[20]、大菱鲆[21]、牙鲆(Paralichthys olivaceus)[22-23]和大黄鱼[11]等某一阶段的生长性能进行了比较。但关于鱼类BLUP家系选育中各阶段选育家系生长性能的比较，目前还未见报道。该研究在福瑞鲤继续选育过程中，通过对选育家系群各生长阶段生长性能以及越冬成活率的比较，观察BLUP家系选育在福瑞鲤继续选育中的潜力和效果，并为这一综合育种方法提供遗传学基础。
1. 材料与方法
1.1 实验鱼及家系设计
实验在中国水产科学研究院淡水渔业研究中心宜兴屺亭科研实验基地进行，时间从2012年3月到2014年3月，为福瑞鲤继续选育的第二世代。亲本选配时，根据BLUP法估算的上一代选育家系育种值从大到小，选取亲缘关系较远的雌、雄鱼各85尾，作为选育系亲本，建立85个选育家系，分别为选育系1~85。同时选取上一代对照家系平均育种值且亲缘关系较远的雌、雄鱼各20尾，作为对照系亲本，建立20个对照家系，分别为对照系1~20。按得到的亲本配对方案挑选雌、雄鱼进行人工催产繁殖。
1.2 家系培育及数据采集
对选择的亲本进行人工催产，采用自然受精产卵的方式进行繁殖，按雌雄鱼1 : 1的比例将不同家系的亲本放入不同的网箱内进行隔离繁殖，产卵后将鱼巢移到另一个网箱中孵化出苗。实际生产了70个选育家系和12个对照家系，按育种值从大到小分别命名为选育系1~70和对照系1~12。继续培育至2012年7月17日(4月龄)，从每个家系中随机选取50尾鱼进行PIT(passive integrated transponder)标记，并分别测量每条鱼的体质量(body weight，BW)、体长(body length，BL)、体高(body height，BH)和体厚(body thickness，BT)。在室内水泥池暂养1~2周后，将其放入室外0.33 hm2的同一土池中混养，在原池越冬，越冬期间适量投喂。分别在2012年12月(9月龄)越冬前和2013年5月(14月龄)越冬后以及第二年2013年12月(21月龄)越冬前和2014年3月(24月龄)越冬后进行标记扫描并测量每条鱼的BW、BL、BH和BT。分别用BH/BL和BT/BL来观察福瑞鲤体型的变化。根据越冬前后标记扫描情况计算越冬成活率。为了便于数据整理呈现，将70个选育家系按照育种值从高到低划分为A、B、C、D和E等5个组，分别代表生长快速组(1~14家系)、生长较快组(15~28选家系)、生长一般组(29~42家系)、生长较慢组(43~56家系)和生长慢速组(57~70家系)。
1.3 数据处理与分析
实验结果用平均值±标准误(X±SE)表示。体质量、越冬期的成活率、BH/BL和BT/BL分别用SPSS 22.0软件包进行单因素方差分析(One-Way ANOVA)，并对差异显著者进行Duncan′s多重比较，显著水平为P < 0.05。同时进行相关性和主成分分析。
2. 结果与分析
2.1 不同家系群各生长阶段体质量的差异分析和相关性分析
4月龄时选育系B和C组福瑞鲤的体质量之间无显著差异(P>0.05)，但显著高于选育系A、D、E组和对照系(P < 0.05)(表 1)。而经过第一个快速生长期到9月龄时，选育系A、B、C组鱼的体质量之间无显著差异(P>0.05)，但选育系B组鱼的体质量显著高于D、E组和对照系(P < 0.05)。经过第一个越冬期，各家系组鱼的体质量均有所增加，但无显著差异(P>0.05)。经过第二个快速生长期到21月龄时，选育系A组福瑞鲤的体质量已经最大，且显著高于D、E组和对照系(P < 0.05)。经过第二个越冬期到达到24月龄时，选育系A组鱼体质量和B、C组无显著差异(P>0.05)，但显著高于D、E组和对照系(P < 0.05)。
表 1 福瑞鲤不同家系群各生长阶段体质量比较Table 1. Comparison of body weight of different FFRC strain common carp family groups at different growth stages家系
family体质量(平均值±标准误)/g body weight(X±SE) 4月龄
4-month-old9月龄
9-month-old14月龄
14-month-old21月龄
21-month-old24月龄
24-month-old选育系selection family group A 18.39±0.60a 237.2±7.18bc 250.7±8.18 942.2±27.2c 995.1±30.5c B 20.29±0.58b 239.9±7.22c 246.1±7.51 900.6±23.4bc 968.0±40.2bc C 21.27±0.67b 234.0±7.62bc 243.3±7.96 891.5±25.0bc 947.9±28.5abc D 17.63±0.86a 217.1±7.74ab 227.0±8.08 815.7±24.6a 869.4±27.4a E 17.59±0.79a 214.8±6.62ab 225.6±7.41 844.7±21.7ab 886.8±26.5a 对照系control family group 18.29±0.80a 211.3±6.17a 225.3±7.24 836.0±23.8ab 878.2±27.2a 注：同列标注不同小写字母表示差异显著(P < 0.05)。 Note：In the same colume，values with different small letter superscripts indicate significant difference (P < 0.05). 在此基础上，对福瑞鲤各生长阶段体质量间的相关性进行了分析(表 2)。9月龄、14月龄、21月龄鱼的体质量与24月龄体质量的相关系数的显著性均达到了极显著水平(P < 0.01)，分别为0.851、0.897和0.957(表 2)。且只有4月龄和21月龄、24月龄体质量间的相关系数为显著水平(P < 0.05)。
表 2 福瑞鲤各生长阶段体质量间的相关系数Table 2. Correlation coefficients of body weight of FFRC strain common carp at different growth stages体质量
body weight4月龄
4-month-old9月龄
9-month-old14月龄
14-month-old21月龄
21-month-old24月龄
24-month-old4月龄4 month-old 1.000 0.448** 0.373** 0.236* 0.251* 9月龄9 month-old 0.448** 1.000 0.955** 0.842** 0.851** 14月龄14 month-old 0.373** 0.955** 1.000 0.900** 0.897** 21月龄21 month-old 0.236* 0.842** 0.900** 1.000 0.957** 24月龄24 month-old 0.251* 0.851** 0.897** 0.957** 1.000 注：*.差异显著(P < 0.05)；* *.差异极显著(P < 0.01) Note：*. significant difference (P < 0.05)；* *. very significant difference (P < 0.01) 2.2 不同家系群各生长阶段体型比较
通过体厚/体长和体高/体长2个参数比较了不同家系福瑞鲤各生长阶段的体型变化(表 3和表 4)。21月龄时福瑞鲤选育系A组福瑞鲤的体厚/体长显著高于选育系B、D组和对照系(P < 0.05)，其他各生长阶段，各家系间的体厚/体长无显著差异(P>0.05)(表 3)。而随着福瑞鲤生长时间的延长，其体厚/体长值也逐渐增加，且各家系组表现出了相同的趋势。9月龄以后的福瑞鲤体厚/体长显著高于4月龄(P < 0.05)，9月龄和14月龄越冬期间并无显著变化，到21月龄时，选育系A组福瑞鲤的体厚/体长值显著增加(P < 0.05)，到24月龄时，各家系组福瑞鲤的体厚/体长值均达到了最高(P < 0.05)。
表 3 福瑞鲤不同家系群各生长阶段体厚/体长比较Table 3. Comparison of body thickness/body length of different FFRC strain common carp family groups at different growth stages家系
family体厚/体长(平均值±标准误) body thickness/body lenth(X±SE) 4月龄
4-month-old9月龄
9-month-old14月龄
14-month-old21月龄
21-month-old24月龄
24-month-old选育系selection family group A 0.161±0.002a 0.179±0.002b 0.179±0.002b 0.184±0.002Bc 0.197±0.006d B 0.159±0.001a 0.176±0.002b 0.178±0.004b 0.178±0.002Ab 0.195±0.008c C 0.160±0.002a 0.181±0.004b 0.177±0.002b 0.182±0.002ABb 0.195±0.004c D 0.160±0.004a 0.178±0.002b 0.179±0.004b 0.179±0.003Ab 0.195±0.007c E 0.160±0.002a 0.180±0.002b 0.180±0.002b 0.180±0.004ABb 0.196±0.006c 对照系control family group 0.158±0.002a 0.176±0.002b 0.175±0.002b 0.177±0.002Ab 0.197±0.010c 注：同行不同小写字母表示生长阶段的差异显著(P < 0.05)；表 4同此。 Note：In the same line，values with different lowercase superscripts indicate significant difference (P < 0.05)；the same case in Tab. 4. 表 4 福瑞鲤不同家系群各生长阶段体高/体长比较Table 4. Comparison of body height/body length of different families of FFRC strain common carp family groups at different growth stages家系
family体高/体长(平均值±标准误) body height/body length(X±SE) 4月龄
4-month-old9月龄
9-month-old14月龄
14-month-old21月龄
21-month-old24月龄
24-month-old选育系selection family group A 0.321±0.002c 0.315±0.004c 0.304±0.002b 0.286±0.003a 0.300±0.007Bb B 0.320±0.005c 0.317±0.007c 0.302±0.006b 0.281±0.002a 0.293±0.002ABb C 0.320±0.002c 0.318±0.007c 0.300±0.003b 0.285±0.002a 0.292±0.003ABab D 0.322±0.006d 0.312±0.003cd 0.302±0.006Bc 0.282±0.003a 0.293±0.005ABb E 0.323±0.006c 0.321±0.003c 0.306±0.007b 0.287±0.003a 0.298±0.002ABab 对照系control family group 0.316±0.002c 0.312±0.003c 0.300±0.002b 0.286±0.009a 0.290±0.002Aab 24月龄时福瑞鲤选育系A组鱼的体高/体长显著高于对照系(P < 0.05)，其他各生长阶段，各家系间的体高/体长无显著差异(P>0.05)(表 4)。而与体厚/体长的变化趋势不同的是，随着生长时间的延长，各家系组福瑞鲤的体高/体长值降低。第一个越冬期过后的14月龄，福瑞鲤的体高/体长已显著降低，到21月龄时降到最低点(P < 0.05)。
2.3 不同家系群越冬期的成活率比较
鱼类越冬期成活率也是选育的重要指标之一，越冬能力的强弱直接影响选育的成功与否。福瑞鲤2个越冬期的成活率各家系组间无显著差异(P>0.05)，其成活率均达到了94%以上(表 5)。
表 5 福瑞鲤不同家系群越冬成活率的比较Table 5. Comparison of survival rate of different FFRC strain common carp family groups during overwintering period家系
family第一个越冬期成活率/%
survival of 1st overwintering period第二个越冬期成活率/%
survival of 2nd overwintering period选育系selection family group A 97.7±0.70 96.5±0.78 B 97.4±0.65 95.9±0.71 C 98.1±0.37 95.8±0.82 D 97.0±0.72 96.1±0.83 E 97.2±0.96 94.5±1.04 对照系control family group 96.7±0.76 96.4±0.94 2.4 福瑞鲤生长性状的主成分分析
对福瑞鲤家系群的BW、BL、BT和BH 4个生长性状进行了主成分分析，每个性状在各主成分的信息量及特征值见表 6。前3个主成分的贡献率分别为41.72%、23.83%和20.21%，累计贡献率达到85.76%。其中第一主成分起主要作用的是体质量，第二主成分起主要作用的是体长，第三主成分起主要作用的是体厚，第四主成分起主要作用的是体高。
表 6 福瑞鲤生长性状的主成分分析Table 6. Principal components analysis for four morphometric characteristics of FFRC strain common carp项目
item第一主成分
the first principal component第二主成分
the second principal component第三主成分
the third principal component第四主成分
the fourth principal component体质量BW 0.61 -0.06 -0.25 -0.75 体长BL 0.28 0.93 0.20 0.09 体厚BT 0.46 -0.32 0.82 0.13 体高BH 0.58 -0.13 -0.48 0.64 贡献率/% total contribution rate 41.72 23.83 20.21 14.25 3. 讨论
福瑞鲤是经1代群体选育和连续4代BLUP家系选育成功获得的鲤新品种，其最主要的特点是生长速度快、体型好。为了防止遗传混杂引起的生长衰退，并进一步观察BLUP家系选育在其继代选育中的潜力，该研究对福瑞鲤继续选育的第二世代进行了全面监测，比较了福瑞鲤选育家系群各发育阶段的生长差异。结果表明生长快速家系在早期(4月龄)生长速度较慢，到后期(9月龄)则快速生长，体质量增长表现出了明显的优势。原因可能是福瑞鲤4月龄前各家系是网箱隔离养殖，而生长速度除受亲本基因型等自身遗传背景影响，可能还受到环境因素的影响。韦信键等[11]在大黄鱼家系早期阶段生长性状的比较中发现，不同月龄各个家系的体质量表型值排序存在不一致性，认为其除了受家系遗传差异影响外，可能还受到环境因素的影响。户国等[24]也认为在虹鳟实际育种过程中，环境的影响可能错误地放大了不同家系之间的遗传差异，从而可能会降低选择的准确性及效率。而后期的快速生长可能是由于某种补偿机制引起的。补偿生长是指动物机体在经历一段时间的限制生长后，为达到生长未受限制的动物的体质量所进行的一个加速生长的生理过程[25]。董在杰[2]在鲤不同育种群体的补偿生长研究中发现，其不同的生长阶段具有体质量补偿，补偿生长不仅显著影响到收获体质量和增重，对体型也产生了一定的影响。该研究中，随着养殖时间的延长，福瑞鲤的体厚/体长增加，体高/体长降低，验证了其修长的体型特点。而衡量福瑞鲤新品系的选育效果除了体型和生长性能优劣之外，越冬能力也是关注的重点，此研究中各家系群福瑞鲤2个越冬期的成活率均在94%以上。在其他鱼类中，GALL和BAKAR[26]采用BLUP育种法对尼罗罗非鱼进行了连续3代的选择，遗传进展比对照群体提高了40%。NEIRA等[27]在银大麻哈鱼(Oncorhynchus kisutch)生长性状的遗传改良中，通过动物模型和BLUP法进行连续4代的人工选择，其平均每一代体质量的遗传进展比基础群体提高了13.9%。李镕等[9]釆用动物模型BLUP法对大口黑鲈进行选择，发现每一生长阶段育种值选择的效率均高于表型值选择。可见通过BLUP家系选育的途径进行福瑞鲤继续选育是可行和成功的。
对鱼类进行遗传改良时，合适的个体选择时期已在一些鱼类中有所探讨。王新安等[21]认为大菱鲆选择育种时，进行个体选择的时期应不低于9月龄。此研究对福瑞鲤生长性状进行主成分分析发现，体质量是对福瑞鲤生长性能影响最大的因素，其贡献率达到41.72%，其次是体长，贡献率为23.83%。在此基础上对不同生长时期的体质量进行相关分析，发现在2龄鱼阶段内，9月龄、14月龄、21月龄鱼的体质量与24月龄的相关系数的显著性均达到了极其显著水平(P < 0.01)，分别为0.851、0.897和0.957。且月龄越长，福瑞鲤此月龄的体质量对下一月龄体质量的影响越大。同时9月龄福瑞鲤的体厚/体长已显著增加，14月龄的体高/体长已显著降低。因此，在采用BLUP家系育种技术对福瑞鲤进行继续选育时，进行早期个体选择值得尝试。至于最为适合的选择时间点，有待于进一步研究。
-
![]()
图 1 水下洗网机有限元模型建立流程
a.工程设计图；b.几何图；c.有限元模型
Figure 1. Process of establishing finite element model of net cleaning machine
a.engineering design; b.geometrical drawing; c.finite element model
![]()
图 6 洗网机出口路径上的速度分布曲线
Figure 6. Distribution of flow velocity on outlet path of net cleaning machine
![]()
图 7 洗网机出口处压力分布图
Figure 7. Distribution of flow pressure at the outlet of net cleaning machine
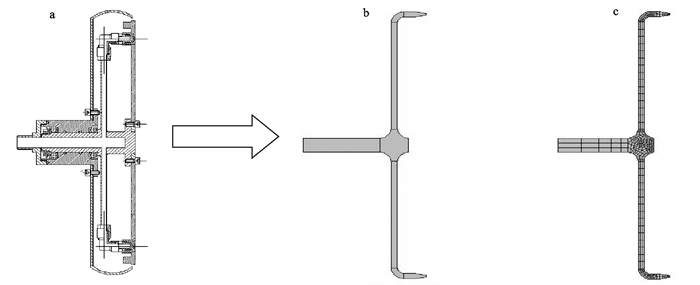
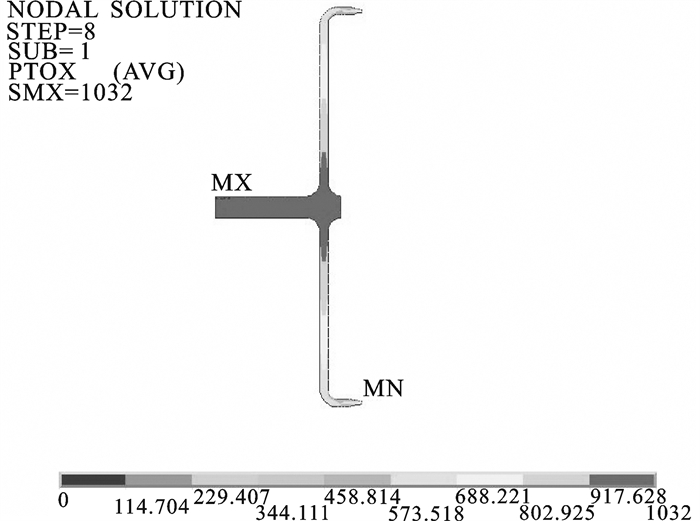
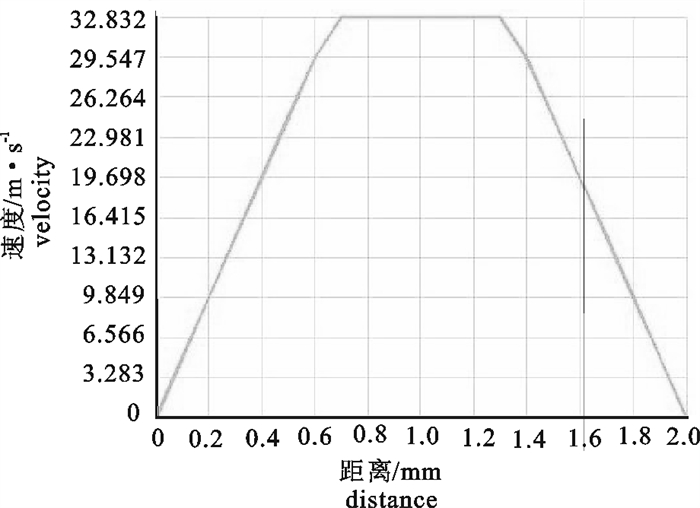
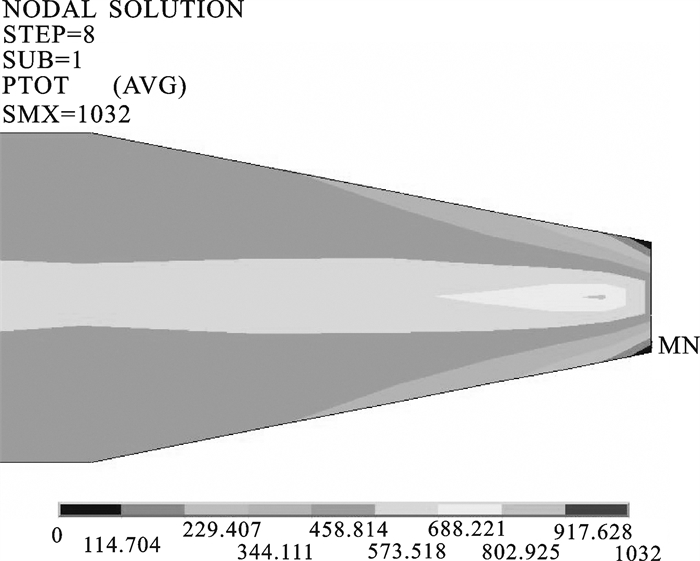
表 1 洗网机工况参数以及流体性质参数
Table 1 Work condition parameters and fluid properties of net cleaning machine
流量/L·min-1
flow flux海水密度/kg·m-3
sea-water density动力粘度/kg·(m·s)-1
kinematic viscosity初始速度/m·s-1
initial velocity出口相对压力/Pa
relative pressure of outlet100 1.023×103 1.345×10-3 8.3 0 
下载: 导出CSV
-
[1] 胡昱, 郭根喜, 黄小华, 等. 高压射流式水下洗网机喷嘴的设计[J]. 南方水产, 2008, 4(4): 16-20. doi: 10.3969/j.issn.2095-0780.2008.04.003 [2] 杨国来, 周文会, 刘肥. 基于FLUENT的高压水射流喷嘴的流场仿真[J]. 兰州理工大学学报, 2008, 34(2): 49-52. doi: 10.3969/j.issn.1673-5196.2008.02.012 [3] 苏铭德, 黄素逸. 计算流体力学基础[M]. 北京: 清华大学出版社, 1997: 71-72. https://www.zhangqiaokeyan.com/book-cn/081504343534.html [4] 张国强, 吴家鸣. 流体力学[M]. 北京: 机械工业出版社, 2005: 137-138. [5] 周宁. ANSYS机械工程应用实例[M]. 北京: 中国水利水电出版社, 2006: 275-296. https://hn.sslibrary.com/user/login/showlogin?backurl=%2Fshowbook.do%3FdxNumber%3D11631760%26d%3D5A5F610C2DAAA4D094529FC69A4CE849%26fFenleiID%3D0T0H0000 [6] 许洋, 党沙沙, 胡仁喜. ANSYS11.0/FLOTRAN流场分析实例指导教程[M]. 北京: 机械工业出版社, 2009: 134-142. https://www.zhangqiaokeyan.com/book-cn/08150362019.html [7] 袁莉. 基于ANSYS通风机流场的仿真[J]. 煤矿机械, 2007, 28(1): 49-50. doi: 10.3969/j.issn.1003-0794.2007.01.020 [8] 李萍, 仇涤凡, 赵英杰. 基于ANSYS/FLOTRAN的喷头流道压力损失的有限元分析[J]. 辽宁石油化工大学学报, 2007, 27(4): 48-50. doi: 10.3969/j.issn.1672-6952.2007.04.014 [9] 林近山, 马汝建, 赵东, 等. 风机内空气流动仿真研究[J]. 济南大学学报: 自然科学版, 2005, 19(3): 255-257. doi: 10.3969/j.issn.1671-3559.2005.03.018 -
期刊类型引用(10)
1. 王彦云，王济世，刘晓夏，赵璐瑶，杨曙明. 基于SNP标记的黄河鲤鉴定研究. 水产学杂志. 2022(03): 7-14 . 
百度学术
2. 苏玉红，沈玉帮，鲍生成，郭加民，张家华，谢楠，刘凯，徐晓雁，李家乐. 青鱼不同地理群体生长差异比较分析. 淡水渔业. 2021(03): 20-26 . 百度学术
3. 樊海平，薛凌展，杨晓燕，钟全福，秦志清，黄德荣，张树兴. 投饵与不投饵稻田养殖‘福瑞鲤’经济效益分析. 中国农学通报. 2020(08): 155-159 . 百度学术
4. 马冬梅，黄樟翰，朱华平，谢骏. 广东粤北地区禾花鱼的形态特征及遗传学分析. 渔业科学进展. 2019(02): 33-42 . 百度学术
5. 沈夏霜，敖秋桅，谭芸，甘西，梁军能，罗永巨，朱佳杰. 4个品系罗非鱼生长性能的比较. 江苏农业科学. 2019(10): 193-196 . 百度学术
6. 甘宝江，张盛，韦玲静，黄杰，莫洁琳，甘习军，滕忠作，叶香尘. 广西稻田养殖金边鲤群体遗传多样性分析. 水产科学. 2019(05): 636-646 . 百度学术
7. 王磊，施文瑞，宋东蓥，马晓，吴利敏，李学军，陈军平，张世杰，孙亚威，许莎诺. 淇河鲫不同家系生长性能的比较. 淡水渔业. 2018(03): 47-52 . 百度学术
8. 陈军平，王娅，王磊，樊云鹏，张世杰，许沙诺，齐如意，张红，高兴磊. 淇河鲫家系早期生长性能的比较. 河南水产. 2018(01): 18-21 . 百度学术
9. 杨月静，向梦斌，叶祥益，张争世，罗辉，叶华. 齐口裂腹鱼SNP标记与生长性状的关联分析. 中国水产科学. 2018(02): 278-285 . 百度学术
10. 廖愚，王培培，袁宗伟，杨宾兰，郑海涛，卢飞麟，吕业坚，覃俊奇. 不同养殖模式建鲤家系选育F_3代生长性能比较分析. 西南农业学报. 2017(12): 2843-2848 . 百度学术
其他类型引用(2)
计量
- 文章访问数:
- HTML全文浏览量:
- PDF下载量:
- 被引次数: 12
粤公网安备 44010502001741号
